534A - Экзамен
Легко убедиться в том, что k = n для всех n ≥ 4. Существует множество алгоритмов, позволяющих построить нужную последовательность длины n при n ≥ 4. Например, можно сажать студентов слева направо, при этом сначала сажать студентов с нечетными номерами в порядке убывания, начиная с самого большого нечетного номера, а затем аналогично ставить студентов с четными номерами. В такой последовательности модуль разности между двумя соседними нечетными (или двумя четными) номерами будет равна 2, а единственная пара соседних нечетного и четного номера будет образовывать разность, большую 3 (поскольку n ≥ 4).
Случаи n = 1, n = 2, n = 3 рассматриваются отдельно, и ответы для них равны 1, 1, 2 соответственно. Асимптотика решения — O(n).
Авторское решение: 10691992
534B - Пройденный путь
Покажем, что в каждую секунду i (0 ≤ i ≤ t - 1) максимально возможная скорость равняется 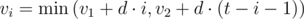 . Действительно, если бы значение vi было больше, то автомобиль не успел бы разогнаться или затормозить вовремя. Тот факт, что разность между соседними vi при такой формуле не превышает d по модулю каждый может доказать самостоятельно.
. Действительно, если бы значение vi было больше, то автомобиль не успел бы разогнаться или затормозить вовремя. Тот факт, что разность между соседними vi при такой формуле не превышает d по модулю каждый может доказать самостоятельно.
Пользуясь вышеописанной формулой, можно просто перебрать i от 0 до t - 1 и просуммировать значения vi, получая асимптотику решения O(t).
Возможно написать немного другое решение, которое пользуется следующим фактом. Если до конца пути осталось t секунд, текущая скорость равна u, а скорость в конце должна быть равна v2, то существует способ доехать до конца пути требуемым образом тогда и только тогда, когда |u - v2| ≤ t·d. Имея этот критерий существования ответа, можно просто каждый раз пытаться перейти к следующей секунде, выбирая максимальную из скоростей (просто в цикле от u + d до u - d), чтобы из состояния на следующей секунде был способ дойти до конца пути.
Авторские решения: 10692136 и 10692160
534C - Кости Поликарпа
Решение задачи использует факт, что с помощью k костей d1, d2, ..., dk можно набрать любую сумму от k до  . Это легко объясняется тем, что если существует способ набрать сумму s > k с помощью костей, то существует способ набрать сумму s - 1, который получается уменьшением значения одной кости на 1.
. Это легко объясняется тем, что если существует способ набрать сумму s > k с помощью костей, то существует способ набрать сумму s - 1, который получается уменьшением значения одной кости на 1.
Обозначим сумму значений всех n костей как 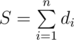 . Зафиксируем очередную кость di (значение на ней обозначим как x (1 ≤ x ≤ di). С помощью остальных костей мы можем набрать сумму s (n - 1 ≤ s ≤ S - di). Мы знаем, что общая сумма s + x = A, а значит n - 1 ≤ A - x ≤ S - di, откуда следует, что A - (n - 1) ≥ x ≥ A - (S - di).
. Зафиксируем очередную кость di (значение на ней обозначим как x (1 ≤ x ≤ di). С помощью остальных костей мы можем набрать сумму s (n - 1 ≤ s ≤ S - di). Мы знаем, что общая сумма s + x = A, а значит n - 1 ≤ A - x ≤ S - di, откуда следует, что A - (n - 1) ≥ x ≥ A - (S - di).
С помощью вышеописанных неравенств для каждой кости вычисляется отрезок возможных значений, с помощью которого вычисляется количество значений, которые выпасть не могли. Асимптотика решения — O(n).
Авторское решение: 10692192
534D - Рукопожатия
Очевидно, порядок чисел в последовательности a значения не имеет. Ниже будем считать, что порядок чисел совпадает с порядком появления в ЦОПП соответствующих студентов (т.е. сначала пришел студент с индексом 1, потом 2 и так далее).
Для того, чтобы итоговая последовательность чисел ai удовлетворяла условию задачи, необходимо и достаточно, чтобы выполнялись условия ai + 1 ≤ ai + 1 и  . Для построения такой последовательности можно воспользоваться следующим жадным алгоритмом: первым числом, очевидно, поставим 0, а среди всех возможных вариантов последующих чисел ai + 1 будем выбирать максимальное, удовлетворяющее вышеописанным условиям (т.е. первое число, меньшее либо равное ai + 1, имеющее такой же остаток от деления, как и ai + 1). Корректность такого алгоритма обосновывается тем, что любую правильную последовательность можно привести к такому же виду с помощью перестановки чисел последовательности.
. Для построения такой последовательности можно воспользоваться следующим жадным алгоритмом: первым числом, очевидно, поставим 0, а среди всех возможных вариантов последующих чисел ai + 1 будем выбирать максимальное, удовлетворяющее вышеописанным условиям (т.е. первое число, меньшее либо равное ai + 1, имеющее такой же остаток от деления, как и ai + 1). Корректность такого алгоритма обосновывается тем, что любую правильную последовательность можно привести к такому же виду с помощью перестановки чисел последовательности.
Реализовать такой алгоритм можно, если исходные числа поделить на три части по остатку от деления, и с помощью, например, структуры данных ''множество'' быстро находить следующее число за  . Общая асимптотика такого решения —
. Общая асимптотика такого решения —  . Решение можно ускорить до линейного, воспользовавшись принципом сжатия путей.
. Решение можно ускорить до линейного, воспользовавшись принципом сжатия путей.
Авторское решение: 10692252
534E - Берляндская система локального позиционирования
Предположим, что автобус начинал движение в остановке с номером 1 и промоделируем отрезок движения автобуса по m остановкам. Посчитаем для каждой из n остановок, сколько раз ее посетил автобус. Проверим, подходят ли эти количества к входным данным и обновим ответ, если нужно. Теперь попробуем сдвинуть стартовую остановку на остановку с номером 2. Поскольку отрезок пути автобуса должен иметь фиксированную длину, сдвинуть вперед нужно и последнюю остановку, смоделировав движение автобуса еще на одну остановку (после последней остановки).
Таким образом, чтобы получить количества остановок, сдвинув стартовую остановку на одну вперед, нужно сделать обновления всего для четырех остановок. Каждый раз, сдвигая стартовую остановку таким образом, нужно обновлять ответ. Стоит учесть, что всевозможных стартовых остановок (учитывая направление движения) ровно 2n - 2.
Асимптотика решения — O(n).
Авторское решение: 10705354
534F - Упрощенный японский кроссворд
Задачу можно решать несколькими способами.
Один из них можно описать следующим образом. Разделим поле кроссворда на две примерно равные части по столбцам (n × k и n × m - k). Решим для каждой части поля задачу отдельно с помощью перебора (который учитывает ограничения на количества блоков в столбцах) с запоминаниями по количествам блоков в строках. Поскольку каждая часть поля, в худшем случае, имеет размер 5 × 10, всевозможных полей с ограничениями на количество блоков будет не очень много. Посчитав все варианты полей для левой и правой половины поля, нужно перебрать левую часть поля и подобрать возможную правую часть (с учетом ограничений на количества блоков в строках). Такое решение требует аккуратной реализации автора.
Так же возможно решение с использованием динамики по профилю, где профиль — количество блоков в строке.
Авторское решение пользуется обеими идеями: 10705343











В D можно обойтись без множества. Можно при текущем ai следующее искать таким образом, если есть ai + 1, то выберем его, иначе проверим, есть ли ai - 2, далее ai - 5 и т.д. Такой алгоритм будет работать за O(n), так как если мы "спустимся" до ai - j на каком-то шаге, то мы больше никогда не поднимемся выше, чем ai - j + 2. Если я не ошибся :)
Красивое и простое решение для Е.. интересно как решали другие участники?
Я сначала разделил m на период (2n-2) с остатком и вычел соответствующие числа из количеств посещений остановок (по одному для крайних остановок и по 2 для остальных). Оставшееся число посещений (на остатке) всегда 0, 1 или 2, причем возможных вариантов всего несколько: 0..011...110..0, 0..01..12..21, либо 12...21...12...21. В каждом из них однозначно определяются начальная и конечная остановка и длина маршрута. Осталось прибавить длину периода (она не зависит от начальной остановки). Ну и случай, когда остаток нулевой, особенный.
А я не делил на период, а посчитал вхождение в каждую остановку. Дальше если количество вхождений в две соседние остановки разное — будем считать, что наиболее тяжелая из них — это возможный старт автобуса. Ну и докинем еще остановки 1 и n в список возможных стартов. Таким образом, у нас есть максимум 4 возможных начала пути автобуса, проэмулируем от каждого из них поездку влево и вправо, проверим корректность полученной эмуляции входным данным. Если все хорошо, добавим полученный ответ в список возможных ответов. Если все найденные ответы совпали — выводим, иначе -1.
Работает дольше, но случаев разбирать меньше. Или в этой идее есть косяк?
Должно работать вроде. Но особый случай (когда все внутренние остановки встретились одинаковое число раз) надо все равно разобрать отдельно.
Как я понимаю, это случай, когда мы могли начать с любой остановки? Тогда да, у жюри не было теста, где расстояние (1,2) == (n,n-1), а в середине различалось.)
The submission links for E and F don't work. Probably because you submitted them as a contest manager?
Fixed, sorry for that.
Yernat Bekzat is !!!
Deleted
For D, I think many contestants have better (more elegant) solutions than the Jury's solution.
My solution for E is to simulate the following cases
Special handling for K 2K 2K .. 2K K: check if all distances are equal. If yes it can be uniquely determined. It not, output -1.
Yeah D looks a little like an overkill to me...
Thanks for your E explanation, in the middle of the contest I thought it could be reduced to fewer cases, what do you think?
Can someone explain D to me? I tried a lot and read all the comments on the announcement blog post as well but could not understand how to solve it.
I will try my best, take the example case 3:
4 0 2 1 1
Let us regroup the input based on the amount of preconditions every person has (0 2 1 1) -> (1), (3 4), (2), the numbers you see now are the indexes (starting with 1), not the preconditions.
All the problem is based on, when could I regroup 3 people to conform a team? Does it matters which guys will conform it?
Well, the second question is easier, it doesn't matter which guys (who are already in the room) team up together. For the other question, you can build a team as soon as a person with the highest precondition enters the room... Why? Because there is no other way to accept lower precondition people to enter, unless of course you kick out some guy, but then again, that's not possible, the only thing you can do to reduce the max level, is to group 3 people.
Take a look at this http://codeforces.me/contest/534/submission/10685298 it follows the same idea here, hope code is clearer than my explanation.
Thanks for the explaination. I saw your submission earlier as well but could not get why the dfs works.
Which I did during competition was to draw the graph, then I noticed there were some vertices where I got stuck, and I could not move forward (keep letting people into the room) if I didn't get to lower vertices.
That's why I am moving in a "level-3" fashion whenever I get stuck, this means I need to build a team, so I can progress with the rest of the guys which are not still on the room.
I have a question about problem D. Many solutions and even editorial solution are using modular calculation, which means handshakes can be dropped more than 3 at one time. (your submission also makes it possible to jump from 100 to 1 etc.) But the description says "Different teams could start writing contest at different times." and what I understood was only one team can be created at one time thus the choice between -2(-3+1, creation of team and entering) and +1. Am I misunderstanding it?:(
Handshakes can go to MAX (where MAX is the total of people) and return to 0 if necessary, then again notice that we are discarding the students with the highest preconditions first.
MAX/3 teams could be created at the same time as I understand, I mean, there is no restriction about how many teams can be formed between a pair of students entering the room.
"Different teams could start writing contest at different times." It still seems somewhat ambiguous to me.. What does this statement mean then? Confused...:(
It means to me that [0, N/3] teams, where N is the amount of people in the room, can be created at ANY time. The redaction sometimes is not the best, but I guess that is the message.
Assume that at the end of the day there were 5 teams, well, those teams could have been formed (and started participating) at different times... is that better?
I thought it meant that x≠y → t_x≠t_y. where x,y are team number and t_x is the time the team created. I think I totally misunderstood it. I got the idea of yours! Thanks for kind explanation.
Не могу посмотреть посылки по D и E: Недостаточно прав для просмотра запрошенной страницы
For problem D, please check another solution : 10686351 , much easier
В задаче F количество всевозможных полей 5*10, генерируемых перебором, учитывающим только столбцы, будет 15^10. Если в столбце число 1, то есть 15 вариантов как расположить блок (5 высотой 1, 4 высотой 2 и т.д.) Это не очень много?
Looking at the official solution for F, I see it uses meet in the middle.
I was looking at that solution earlier (I also solved that way), and it seems it can solve the problem for m ≤ 30 or even m ≤ 40 since each half can be solved fast enough (lots of accepted solutions did this problem m ≤ 20 without meet in the middle) and the combination is of the same complexity.
So, I was curious why you decided to make the constraints so small. Did you want to allow doing it without meet in the middle?
I don't understand my mistake, pls view, explain me
include<bits/stdc++.h>
define ii pair<long long,long long>
define gt first
define cs second
using namespace std; long long n,kq[200005]; ii a[200005]; bool dd[2000006]; void nhap() { cin>>n; long long i; for(i=1; i<=n; i++) { cin>>a[i].gt; a[i].cs=i; } } void xuli() { sort(a+1,a+n+1); long long i,j; //fill(vt+1,vt+n+1,0); kq[n]=n+1; for(i=1; i<=n; i++) { j=a[i].gt; while (kq[j]!=0) { j=j+3; } kq[j]=a[i].cs; // vt[j]=1; } for(i=0;i<n;i++) {if (dd[kq[i]]==1 || kq[i]==0) {cout<<"Impossible";return;}dd[kq[i]]=1;} cout<<"Possible\n"; for(i=0; i<n; i++) cout<<kq[i]<<" "; } main() { nhap(); xuli(); }
I don't understand my mistake pls check for me :((
I did not understand E. Could someone explain it? Thanks.
Suppose n=6, m=4. We have to find the answer in the series:
[ 1 ( 2 3 4 ] 5 ) 6 5 4 3 2 1 2 3
First check the first 4(=m) numbers. When we push forward, we don't have to check all of the four numbers again but only two numbers: 1(which should be erased) and 5(which should be added). Update the distance by decreasing by dist(1~2) and increasing by dist(4~5). Update the count by decreasing # of 1, increasing # of 5 (by one each). How do we check the match? We know the update of the count only happens in 2 numbers. Other numbers remain. We maintain the difference count of each numbers, counting how many numbers have different count from the given pattern. That different count is 0 means the match.
Got it. Thank you :)
For the problem F, i didn't understand what is meant by 'we do not need same solutions with same number of blocks in rows' Can anyone explain it to me?
534B — Covered Path, in this problem, CAN SOMEONE EXPLAIN how did they get this below formuale ? any maths involved ?
Your text to link here...
(1) The speed during the i-th second cannot be larger than v1 + di because we couldn't speed up from v1 that much.
(2) It can't be larger than v2 + d(t - i - 1), because we won't be able to slow down to v2 during the remaining time.
And because we want to drive as far as possible, the speed must be the maximal value that conforms to (1) and (2), i.e. min(v1 + di, v2 + d(t - i - 1)).
Can someone explain how dp is implemented in problem F ? Thanks in advance!!
Codechef gives better detailed explanation of editorial than codeforces.
Editorial should have detailed explanation.I can't understand problem F.
codeforces editorial's are like hint to the problem.We don't need hint we need explanation.
Could some one please explain why this dp approach is wrong for problem B.
note : rep(a,b) means for(int i = 0 ;i<b;++i)
rep(i,200){ rep(j,200){ dp[i][j] = -INF; } } //memset(dp,-100000000,sizeof(dp)); dp[0][v1] = 0; for(int i = 1;i<=t;++i){ for(int j = 0;j<=110;++j){ for(int l = -d;l<=d;++l){ if((j-l) >= 0 && (j-l)<=110){ if(dp[i-1][j-l] != -INF) dp[i][j] = max(dp[i][j],dp[i-1][j-l] + (j-l)); } } } } cout<<(dp[t-1][v2]+v2)<<endl;don't understand what you mean