ikatanic's blog

Croatian Olympiad in Informatics 2015
By ikatanic, 10 years ago, In English

Join us on Saturday, March 28th, 2015 at 14:00 GMT/UTC for the final round of COCI — Croatian Olympiad in Informatics 2015.

This round will be different that the previous rounds. It will be 5 hours long and there will be only 4 tasks but they will be harder than usual.

Click here to see when the coding begins in your time zone.

  • Vote: I like it
  • +55
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +16 Vote: I do not like it

AFAIK it is 5 hours long, right? :P

→ Reply
»
10 years ago, # |
  Vote: I like it +39 Vote: I do not like it

bump

→ Reply
»
10 years ago, # |
  Vote: I like it +13 Vote: I do not like it

There will be live grading ?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

When will you publish results?

UPD: Published already

→ Reply
»
10 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Is there a reason why tests are given in groups? It feels a little disappointing getting 12/100 points when only 2 testcases failed...

Thanks for the contest anyway, the problems were interesting as usual.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +36 Vote: I do not like it

    That's how it usually is with IOI scoring and such: you need to have a program that really works on everything in a given subtask to get points for it. The organisers probably want to have a similar scoring system... if only the feedback was similar as well...

    → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

What was the solution of Ogledala?

I've implemented O((N + Q)(logM)2) solution but it turned out to be too slow, probably due to giant constant factors :(.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 4   Vote: I like it +5 Vote: I do not like it

    That was the complexity of the intended solution, constant factor is not that big though (it runs in 1/3 of TL). I was aware that there are solutions with same complexity but with bigger constant factors due to use of heavy data structures. In such cases it's good there is 'Test' option on the evaluator (I hope you weren't surprised by the TLE) and big tests were really easy to generate.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I was using couple of stl maps, and heap. Is there any chance to get rid of them?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Of course, one way is to pre-determine all the gaps that will happen in form of triples (gap length, how many such gaps, from which starting gap they result) and just sort them appropriately. Now that easily gives you the length of a gap for any girl that comes, and in which starting gap it will be. It is enough to be able to reconstruct the exact gap position in O((log M)^2).

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          After getting rid of heaps(as your way described above), calculating number of nodes with size x in the subtree of a vertex with size y, without any stl maps, got AC with 3.4 seconds. Still using just stl vectors.

          → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I used bellman-ford to solve a system of difference constraints in problem Kovanice. It seems it's too slow and got TLE.

Can anyone tell me how to solve it correctly? Thanks very much.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    Find the longest path in a DAG(also need a union-find for equal cases). If its length equals N, then they are type 1...N respectively, the rest is simple.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 3   Vote: I like it +8 Vote: I do not like it

      Oh. Thank you...

      The mistake I made was that I didn't union coins with equal weights together. And in that case, the graph is not a DAG, and there will be many edges whose weights are 0.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    What I did was, for each vertex in the DAG (after compressing equality relations), finding the longest path starting and the longest path ending in it. If they sum up to N + 1, one of them is directly the answer for that vertex.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      n-1 you mean right?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +8 Vote: I do not like it

        Depends on whether you consider "length" to be the number of edges or number of vertices.

        → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +16 Vote: I do not like it

Waiting for the official editorial...

The third problem is so difficult. I only came up with a very naive solution that uses balanced tree and heap, which runs in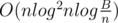 , obviously will get TLE

UPD: I've got the way to reduce a log factor. Notice that when an interval breaks we get two new intervals of same length or with difference 1. And it's easy to see that if every sub intervals break again there will be still at most two possible lengths. Then, we only need to record how many intervals have a certain length, while the exact place could be found further separately(the new subproblem is what is the K-th insertion for an interval originally have length x), also need to pay attention of that slight difference of one: one shorter interval appears at front may generate length N-1 and N, while a little bit longer one after it may got N and N+1, and we need to be especially careful when dealing that length N.

→ Reply
»
10 years ago, # |
  Vote: I like it +37 Vote: I do not like it

My solutions for SIR and CVENK (the two medium problems):

SIR: First, we find the convex hull of peppers in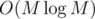 and discard all other peppers. We can use 3 pointers now; two of them are endpoints of the cut and if we move one endpoint E1 ccw along the perimeter of the cheese, we can recalculate the first possible choice for the other endpoint E2 (since the cheese is convex, it means the choice with the maximum area). The third pointer P is at the pepper that makes it impossible to make the area bigger by moving E2 — if we look at the peppers from E1, it's the leftmost vertex we see. The initial value of P and then of E2 for some choice of initial E1 (E2 depends on P, P doesn't depend on E2, so we always re/calculate them in this order) can be found using vector cross products — see my code for details, the area A of the correct part of the cheese can also be found using them; as we move E1 ccw, P and therefore E2 never move cw, which means we only need to recalculate them in O(N + M). As we move E2 or E1, we also need to recalculate A by adding/subtracting the area of some triangle.

CVENK: The fractal is a tree, so we want a compressed version of it that contains all tourists. When we know the tree, we can just root it, count the number of tourists in the subtree of each vertex, find the vertex that doesn't have more than N / 2 tourists in any of its sons' subtrees or outside of its own subtree (if it did, then one of its neighbours gives a smaller answer); that is the centroid and it's sufficient to take either if there are two (there are at most 2), it's the optimal vertex and we just need one DFS from it to compute the answer. It's a well-known problem. For finding the tree, I rewrite the binary representation of (x, y) to a sequence of straight paths from (0, 0), alternating down and right. If we store the sequences that change direction or end at a vertex v of the so far constructed tree, we can look at all that change direction to horizontal, store the lengths of these straight horizontal paths in a set, make new vertices at their endpoints and store for each sequence that it changes direction at a new vertex, with one less straight path in it; similarly for vertical ones. The tree can be constructed recursively this way. Time complexity: there are at most 30N straight paths in each sequence; plus some log-factors from STL map/set, it's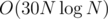 . Finding the answer then only takes linear time.

→ Reply