Пост для тех, кому интересно научиться ещё быстрее искать паросочетание в двудольном графе.
Алгоритм Куна ищет паросочетание в двудольном графе за O(VE). Реализация, данная на emaxx, укладывается в такой шаблон:
forn(i, n) {
fill(used, 0);
dfs(i);
}
Я обычно пишу так:
fill(used, 0);
forn(i, n)
if (dfs(i))
fill(used, 0);
То есть, обнуляю пометки только если нашёл дополняющую цепь. Теперь Кун работает за O(|M|·E), где |M| — размер максимального паросочетания.
Решение можно ускорить ещё как минимум в 2 раза, используя жадную инициализацию паросочетания. Идея: применяем Куна не к пустому паросочетанию, а к паросочетанию размера хотя бы |M| / 2. Кстати, |M| / 2 — оценка снизу, если перед жадной инициализацией сделать random_shuffle, жадность найдёт паросочетание чуть побольше, и Кун будет работать чуть быстрее.
Новое для меня
Оказалось, можно заставить Куна работать ещё в несколько раз быстрее...
fill(pair, -1);
for (int run = 1; run; ) {
run = 0, fill(used, 0);
forn(i, n)
if (pair[i] == -1 && dfs(i))
run = 1;
}
То есть, теперь я не обнуляю пометки даже если нашёл дополняющую цепь.
Я успел потестить на нескольких задачах, например, на задаче про доминошки. Эффект: новая идея без жадной инициализации в 3 раза быстрее старой идеи с жадной инициализацией. Можно скачать тесты и решения и поиграться самостоятельно. Думаете, в доминошках специфический граф? Потестил на произвольном двудольном графе, эффект "на макс тесте в 10 раз быстрее".
Мне эта модификация Куна чем-то напоминает Хопкрофта-Карпа, т.к. получается, что мы за O(E) находим не один путь, а несколько. Непонятно, что стало с асимптотикой алгоритма. Может быть, она тоже улучшилась?)
Спасибо за внимание.











"новая идея без жадной инициализации" — не совсем верно, ведь первая итерация внешнего цикла во внутреннем делает именно жадную инициализацию, сочетая каждую вершину с первым не тронутым (а значит — не сочтенным) соседом.
Да, ты прав. Я имел в виду "без лишнего кода, который обычно появляется, когда мы её добавляем".
Если говорить про константные оптимизации, то как-то не комильфо каждый раз занулять массив
used.Теоретически ты прав. А практически эта оптимизация в данном случае ничего не даст. Например, в последней версии: после того, как я обнулил
used, я делаюforn(i, n) if (...), который работает сильно дольше.Я примерно такими хаками занимался на РОИ 2010 в задаче 3 про самолеты) Пихал Куна вместо того, чтобы решать задачу)
Сдавать сюда удобнее.
Интересно, а я всю жизнь так искал паросочетание и, кстати, всего раз получил ТЛ когда паросочетанием задача-таки сдавалась с алгоритмом Хопкрофта-Карпа. Правда, этот ТЛ был на простом новогоднем контесте, так что не очень считается :) Я, кстати, пару раз пытался сравнить с Диницем и все разы оно (паросочетание Куном) быстрее работало.
"с Диницем" — в смысле, как раз с Хопкрофтом-Карпом? Грамотная реализация Хопкрофта-Карпа отличается от Диницы так же, как Кун от потока — вроде всё тоже самое, но и кода меньше, и работает в 4 раза быстрее.
Ну да, я к тому, что это не была специально заточенная под паросочетание реализация.
А можно посмотреть, что имеется в виду под "грамотной реализацией"?
Авторское решение задачи, о которой ты говоришь ниже. Автор — Олег Давыдов.
Прохладная история про эту оптимизацию.
В ПТЗ как-то была задача (H здесь), которая, по-видимому, задумывалась авторами как простая. Условием была не очень сильно замаскированная просьба посчитать паросочетание в двудольном графе с такими ограничениями: в каждой доле не более 104 вершин, рёбер до 105, мультитест из не более чем 10 тестов, ограничений на сумму чего бы то ни было по всем тестам нет. Особую пикантность добавляло отсутствие тайм-лимита в условии, потому что "как на финале".
Реакцию участников на эту задачу можно оценить по монитору, обратив особенное внимание на зелёный плюсик в первые полчаса (КНУ сдали ровно то, что написано в исходном посте). andrewzta картинно возмущался на всю аудиторию, что мол как же так — задача про паросочетание, ищу Хопкрофт-Карпом, а оно не заходит! (И ещё он обещал обучить этому алгоритму, кажется, итмо 2 или 3.)
Насколько я помню (как один из авторов контеста =), задумывалась она, как "образовательная задача на Хопкрофта-Карпа"
Авторское решение в этой задаче работает не быстрее парсоча, который ты привел в этом посте.
Я верно понимаю, что в последней из приведенных версий парсоча нет смысла в жадной инициализации? Я протестил на паре задач, к которым были тесты — нигде не улучшает больше, чем на погрешность.
Да, ведь на первой итерации внешнего цикла у нас автоматически получится жадная инициализация.
Не совсем, там не только пути длины 1 берутся. Но согласен, что это почти то же самое.
Возможно, это зависит от реализации ДФСа?..
Но в моей — только длины 1. Мы не ищем чередующиеся цепи через вершины, ранее сочтенные на этом шагу, потому что они уже помечены "использованными" тогда, когда были сочтены.
На первый взгляд кажется, что тут по сути на каждом шаге ищется блокирующий набор дополняющих путей, из чего автоматически вытекает асимптотика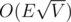 .
.
Насколько я понимаю, не вытекает. Вот если бы мы блокирующий поток из кратчайших путей искали, то да.
Хм, действительно, первый взгляд подвел, ничего автоматически не вытекает.
С Диницем то понятно что надо кратчайшие, я в голове не Диница держал, а некоторые другие соображения, но они тут оказались не к месту.
Еще есть эвристика в написании dfs'a. Вместо чего-то вроде
можно написать два одинаковых цикла: в первом поставить
if (mt[e[v][i]] == -1), а во втором –if (dfs(mt[e[v][i]])). То есть, сначала проверить, нет ли ребра в вершину, не покрытую паросочетанием, и лишь если нет ни одной такой вершины, запускать dfs.В сочетании с основным методом из поста это ускоряет в полтора раза на задаче, обсуждавшейся в этом комментарии.
Звучит здорово, ставлю лайк.
Только по поводу "ускоряет в задаче sociology" есть вопрос.
http://acm.math.spbu.ru/~sk1/problems/sociology_solutions.7z
Содержит несколько решений Куном. В последнем sociology_sk_4.cpp реализована твоя идея.
На большинстве тестов я вижу ускорение в 1.5-2 раза. Но на 32-м тесте решение без твоей идеи работает
time = 3.06cnt = 59 495 427А с ней
time = 2.73cnt = 92 825 80632-й — самый плохой для обоих решений тест.
cnt— сколько суммарно вершин и рёбер мы перебрали за всё время работыdfsОна у нас залита в pcms, туда я и отправляю, тестов у меня нет.
Без этой оптимизации на 32 тесте 0.703с, а макс – на 60, 0.984с.
С ней – на 32 тесте 0.703с (макс), а на 60 – 0.671с.
Код1, код2.
А у меня на 60-м мгновенно.
Я правильно понял, что разница в том, что у меня ещё и жадная инициализация, а у тебя она закомментирована?
Нет, раскомментил жадную эвристику – время работы почти не изменилось в обоих случаях, без двух циклов так и работает ~1.0c на 60 тесте.
Кто нибудь знает кем был Кун? Или какое у него имя? Или откуда он?
https://en.wikipedia.org/wiki/Harold_W._Kuhn
Спасибо)