В этом месте напрашивается эпиграф про удава и попугаев. Тем не менее, ниже вы найдете мою версию ответа на интригующий вопрос из заглавия теста.
Занимаясь подготовкой VK Cup 2015, мы столкнулись с интересной задачей подсчета изменений рейтингов участников в командных контестах. Сразу скажу, что таковых будет немного, и значительного вклада они не должны внести.
Коротко напомню, что рейтинги Codeforces считаются примерно так:
- у каждого участника есть какой-то рейтинг ri на начало раунда,
- так как рейтинг Codeforces наследует идеологию рейтинга Эло, то мы стремимся к оценке, что участник b побеждает участника a с вероятностью:
- зная вероятности микроматчей выиграть/проиграть для каждой пары участников, можно посчитать ожидаемое место участника i (как сумму вероятностей его проигрыша по всем остальным участникам),
- если участник i занимает место лучше ожидаемого, то надо увеличить его рейтинг, иначе — уменьшить.
Это совсем общий принцип, который покрыт противо-инфляционными поправками и некоторыми эвристиками. Кстати, у меня есть большое желание пересмотреть точные формулы с помощью сообщества, попутно сделав рейтинг публичным. Но речь сейчас не об этом, а о том как посчитать рейтинг команды.
Кажется естественной идея распространить текущий подход на командное участие. Одна из проблем — отсутствие правила для вычисления рейтинга команды, если известны рейтинги ее членов. Если бы такое правило было, скажем какая-то функция teamRatings(r1, r2), то довольно логично использовать именно это значение для вычисления ожидаемого места, а потом одинаково изменить рейтинги участников команды в зависимости от того удачным было выступление (лучше ожидаемого места) или нет (хуже ожидаемого места).
Вот такая идея пришла в голову во время обеда команды Codeforces.
Во-первых, искомая функция teamRatings(r1, r2) от рейтингов членов команды должна быть такой, что teamRatings(r1, r2) ≥ max(r1, r2). Кроме того, понятно, что если к tourist-у добавить кого-то не очень сильного (скажем, зеленого участника), то рейтинг команды не должен сильно отличаться от рейтинга tourist-а.
Мной была предложена такая забавная модель. Пусть есть команда AB из двух участников A и B. Попробуем хоть как-то сравнить ее с одиноким участником C. В моей модели вместо командного контеста A + B против C проведем пару встреч A против C и B против C. Если хотя бы в одной из таких встреч победил член команды AB, то засчитаем победу команде, иначе — участнику C.
Конечно, такой подход не учитывает какой-то совместной работы A и B, но хотя бы честно пытается учесть шансы обоих победить C. Если все три рейтинга известны, то легко посчитать вероятность победы C — это произведение вероятностей победить A и победить B. Просто дважды применим формулу Эло и перемножим результаты.
Теперь, когда известен рейтинг C и рейтинг его победы над командой, то, обратив формулу Эло, можно посчитать рейтинг команды.
Есть тонкость, что при таком подсчете рейтинг команды зависит от рейтинга противника C. Как же его выбрать? Можно показать, что при изменении C, результат меняется монотонно. Кажется красивой идея выбрать такое C, чтобы рейтинг команды в конце концов оказался ему и равен. То есть, в качестве противника команде подобрать такого, который играет с командой на равных. Это можно сделать бинпоиском, хотя, наверное, можно и вывести точную формулу (кто поможет?).
В результате получается примерно такой код:
long double getWinProbability(long double ra, long double rb) {
return 1.0 / (1.0 + pow((long double) 10.0, (rb - ra) / 400.0));
}
long double aggregateRatings(vector<long double> teamRatings)
{
long double left = 1;
long double right = 1E4;
for (int tt = 0; tt < 100; tt++) {
long double r = (left + right) / 2.0;
long double rWinsProbability = 1.0;
forn(i, teamRatings.size())
rWinsProbability *= getWinProbability(r, teamRatings[i]);
long double rating = log10(1 / (rWinsProbability) - 1) * 400 + r;
if (rating > r)
left = r;
else
right = r;
}
return (left + right) / 2.0;
}
Полный код можно посмотреть найти по ссылке http://pastebin.com/HnteNGuN
Еще раз отмечу, что какой-то абсолютно справедливой модели посчитать рейтинг команды по рейтингам ее членов мне кажется нет. У меня есть мнение, что это неплохой вариант. Что скажете?
Вот интересные примеры:
| Первый член команды | Второй член команды | Итоговый рейтинг |
|---|---|---|
| tourist, 3239 | Petr, 3045 | 3314 |
| tourist, 3239 | niyaznigmatul, 2700 | 3253 |
| tourist, 3239 | tourist, 3239 | 3392 |
| Petr, 3045 | Petr, 3045 | 3198 |
| tourist, 3239 | Bredor, 1766 | 3239 |
| Bredor, 1766 | Bredor, 1766 | 1919 |
Или вот еще интересное следствие: команда из 3350-ти Бредоров будет решать как tourist.
Заметно, что такой подход, видимо, как-то занижает рейтинг команды (или нет?). Наверное, это не очень страшно — ведь рейтинги команд будут сравниваться почти всегда с рейтингами команд (а команды из одного члена будут, возможно, получать некоторый буст).
Буду рад альтернативным моделям агрегирования рейтингов.
Тут был Рудольф
и?
tourist > Petr+Petr?
This is a philosophical question. But why not? Ratings differ for almost 200. It means that Gennady overcomes Petr with probability ~0.75.
The intuition suggests that a dual-Petr team should solve a contest faster than a single-tourist team because of twice as much problem-solving threads. :)
Идея в стиле тех, кто решает марафонские задачи подбором констант:
После первого раунда с его онлайн-зеркалом можно будет по результатам определить, насколько хороша формула в плане сравнения команд, а так же для сравнения команды против одного участника — и, при необходимости, подобрать формулу получше как-нибудь апостериорно.
Но эта идея не учитывает тот факт, что и по результатам раунда тоже нужно как-то пересчитать рейтинг.
Хотя, в принципе, если это так важно, то можно сначала подобрать формулы, которые более-менее согласуются с результатами, а уже потом пересчитать новые рейтинги.
На счет точной формулы для такого рейтинга команды: мы хотим уравнять команду AB с индивидуальным участником C — то есть по сути сделать вероятность победы каждой из сторон по 0.5. Далее вбиваем полученное в wolframalpha и получаем искомую формулку.
Затем, поигравшись с этой формулкой в том же вольфраме, можно заметить, что рейтинг команды AA равен рейтингу A + 153, не зависимо от рейтинга A, даже не знаю, хорошо это или плохо.
Более того, "прибавка" к рейтингу зависит лишь от разности рейтингов участников, то есть:
Кстати, это необходимое свойство. Если до соревнования игроки имеют рейтинги a и b, а рейтинг команды t(a, b). Пусть после соревнования команда должна иметь рейтинг T. Тогда новые рейтинги игроков определяются как a' = a + T - t(a, b) и b' = b + T - t(a, b). Но должно выполняться T = t(a', b'). Отсюда t(a, b) имеет вид a + f(a - b).
Полагаю, что есть один момент на который стоит обратить внимание — будет ли возможность выбирать членов команды при регистрации как в тренировках? Если один человек по какой-то причине не может участвовать в конкретном раунде, то если нет возможности это указать, это ставит его в проигрышное положение при пересчёте рейтинга, оставляя 2 варианта перед вторым членом команды — писать раунд в одиночестве осознавая что пересчёт ставит его самого в худшее положение и при этом изменяя рейтинг и неучаствовавшего члена команды; или не писать раунд вообще.
Соответственно, при отсутствии возможности указать что этот раунд будет писать только один участник — рейтинг это единственная причина по которой человек оставшийся в одиночку может решить пропустить раунд, а не попробовать пройти дальше в одиночку. К сожалению, некоторых, оказавшихся в подобной ситуации, это может оттолкнуть от написания раунда, что подозреваю не является желаемым побочным эффектом.
Мне кажется, что это очень сильно заниженная оценка силы команды относительно индивидуального участника, тк не учитывает, что у команды по сути вдвое выше скорость решения задач. На модели контеста с кучей простых задач это легко видно, там все решает скорость и с двух компов команда из двух 2200+ будет выигрывать у любого индивидуала с рейтингом до 2500 с легкостью.
Если во всех таких раундах убрать эффект уменьшения стоимости задач со временем (это кстати можно сделать только в рэнкинге для рейтинга, не меняя ничего в рэнкинге для отбора), то модель станет намного ближе к реальности.
Но тогда это повлияет на стратегию команды, потому что теперь особого смысла решать более сложные задачи в начале не будет.
Они конечно пишут быстрее, но ведь ещё должно не упасть.
Я, как участвующий в одного, был бы не против, если бы мой рейтинг пересчитывался вместе с теми, кто решает зеркало (в зеркале ведь по одному участвуют?).
Но, по-моему, что вариант с бустом, что мой вариант, немного нечестные в том плане, что красно-желтые, которые брали себе сине-зеленых в команду, считая, что они ничего не теряют, в таком случае оказываются в неловком положении.
С tourist'ом всё понятно, интересно посмотреть дальше, например взять участников на 20-м и 30-м месте в рейтинге и посмотреть, какой силы должен быть сокомандник у более слабого из пары, чтобы обойти более сильного. Кажется, что 30-й + среднестатистический желтый уже наверняка должны выигрывать у 20-го и т.п. Можно покрутить параметры, глядя на результаты каких-нибудь OpenCup'ов (правда там 3 участника, так что считать сложнее)
Мне вот непонятно, например, почему на TC/CF их рейтинги "меняются" местами.
Если допустить, что командная скорость решения задач примерно равна сумме скоростей всех членов этой команды (а примерно так оно и есть, когда потенциал каждого члена команды эффективно используется во время соревнования), то для решения проблемы с рейтингом команд достаточно найти биекцию между рейтингом и скоростью решения задач.
Формализованное решение: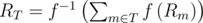
, где RT — рейтинг команды T; Rm — личный рейтинг участика m, члена команды T; f — соответствие между рейтингом и скоростью решения задач.
Конечно, эффективность использования потенциала членов команды во время соревнования должна значительно влиять на успешность команды, а значит и на её рейтинг, но этот параметр едва ли можно выразить через личные рейтинги членов команды. Следовательно определение рейтинга команды только через личные рейтинги его членов в любом случае будет очень грубым...
Также может проявлятся так называемый системный эффект (эмерджентность), выражаемый в том, что скорость команды окажется выше суммы скоростей её членов.
Например, если в команде из двух человек один очень быстро находит идею решения задач, но очень медленно пишет код, а второй — наоборот, то при эффективной кооперации скорость решения задач в коммандном выступлении будет намного выше, чем сумма их скоростей в личных соревнованиях. Так произойдет потому, что личная скорость первого будет определятся очень медленной скоростью написания кода, а личная скорость второго очень медленной скоростью нахождения идеи решения, следовательно сумма их скоростей тоже будет невысокой; но если в команде первый будет искать идею решения, а второй писать код, то скорость команды на самом деле окажется очень высокой.
Системный эффект определяется несводимостью свойств системы к сумме свойств отдельных её частей. Переводя это на проблему вычисления рейтинга команд, можно заключить, что невозможно адекватно вычислить рейтинг команды только через личные рейтинги её участников. Поэтому мне кажется, что рейтинги команд должны вычислятся независимо от рейтингов участников, иначе они будут сильно искажать друг-друга.
Это всё хорошо на бумаге. Но на практике распараллеливание одной задачи между несколькими исполнителями создаёт дополнительные издержки на взаимодействие. Очевидно, что команда из 3 примерно равных по умению участников не решает задачи втрое быстрее каждого из этих участников, даже если предоставить ей 3 компьютера, так как сперва нужно обсудить, кто какую задачу возьмётся решать, и перед каждым переключением задачи необходимо согласовывать это с другими членами команды.
К тому же, ваши измышления можно проецировать только на рутиную деятельность, которая гарантированно будет исполнена по прошествии времени. Далеко не факт, что задача, решённая участником с рейтингом N, окажется по силе команде с рейтингом N. Если бы соревнование состояло из нескольких десятков задач уровня задачи A и надо было их решать на скорость, то ваша формула ещё могла иметь смысл.
Это далеко не очевидно. На примере из этого поста видно, что команда из двух человек может решать задачи хоть в 10 раз быстрее, чем способен каждый из её участников по отдельности, даже если у команды будет только один компьютер. Причем, это не слишком надуманный пример, а вполне вероятный. Можно, конечно, придумать и обратный пример, когда команда будет решать задачи даже медленнее, чем один из её участников: например, если слабый участник команды будет отвлекать сильного ненужными советами.
Так что я и сам понимаю, что предложенный метод очень ограничен, но если всё-таки пытаться считать рейтинг команды только на основании рейтингов её участников, то он очень даже обоснован.
Если между рейтингом участника и количеством успешно решаемых участником задач (например, средней сложности) за единицу времени существует достаточно сильная корреляция, то формула имеет смысл. Нужно просто проверить существование такой корреляции и тогда можно будет делать выводы.
Для полной картины не хватает сравнения с worse :)
Понятно же, что в одном worse 3 туриста
Какой-то велосипед получился. Почему бы просто не сделать расчет рейтинга, считая, что 2 участника из одной команды заняли одно и то же место?
Допустим, в турнире принимают участие команды A+B, C и D+E. Места между командами распределились так: 1. A+B 2. C 3. D+E
Тогда места для индивидуальных участников будут: 1. A 1. B 3. C 4. D 4. E
Проще всего банально не считать рейтинг для команд, состоящих из 2 участников
В командах могут быть сильно разные по силе участники. Такие команды есть. Представим, что Гена включил в команду свою собаку. Она быстренько необоснованно станет красной, если считать, что она заняла топ-место, и при подсчетах учитывать ее текущий рейтинг.
А какой у собаки должен быть рейтинг, если собака не участвует в контестах кроме как в команде с Геной?
Допустим, на двух раундах VK Cup Гена получит +40 (это его максимальное изменение рейтинга за последние несколько контестов). R(Гена)+R(Собака)=R(Гена), поэтому у собаки будет максимум 1580 :)
Возможно я что-то упустил, но я не понял, как будет меняться рейтинг отдельных участников команды, если мы пересчитаем рейтинги команд?
Для обоих членов команды на одну и ту же величину, которая рассчитывается исходя из рейтинга команды и занятого места.
Лично я возражаю. Рассмотрим 3 участника A,B,C и 2 типы задач — X,Y. Пусть A и B состоят в одной команде.
A решает задачи типа X с вероятностью 0.05, а типа Y — 0.9, а B — наоборот — X-0.9, Y-0.05 (при чем так бывает в большинстве случаев), а C — с вероятностью (0.8 0.8). Тогда при таком расчете C окажется НАМНОГО сильнее чем команда (A,B), но A и B вместе — явно сильнее, чем C (A и B — не идиоты, они знают как делить задачи между собой).
Смысл рассуждать о формуле в отрыве от задач, которые будет решать команда из двух. Поясняю на примере двух крайностей которые я вижу, при условии что два участника примерно одного уровня.
Пусть контест состоит из небольшого количества задач, идущих по усложнению, причем в наборе нет задач, которые требуют много времени на реализацию. Тогда, даже если посадить больше чем 2 человека примерно одного уровня, команда упрется в некоторый "потолок" сложности задач. В табличке был пример что (1766, 1766) = 1919. Возможно я ошибусь про уровень задач и рейтинга — давно не писал на рейтинг да и одиночно вообще — но вероятность решить C div1 у одного участника с рейтингом 1919 гораздо выше, чем у двух с 1766, имхо.
Ну и обратная ситуация — большое количество задач, мало времени. Тогда одиночный участник просто может не успеть накодить все то, что успеют в два компьютера два более слабых.
Интересно, какой проблемсет будет сегодня...
What rating would team consisting of 228 Bredors have?
2773
I think that this model is a pretty good first step, it essentially simulates a thinking contests where teammates try to solve the problem individually: the lone programmer has to come up with the idea faster than the fastest member of the team. This doesn't take into account two things:
However, one think is clear: if you keep adding participants their added value decreases. Your formula already gives less probability of winning a team of 3x2000 against a team of 2x2000 than a team of 2x2000 against a team of 1x2000. Nevertheless I think that a better model would raise getWinProbability to a coefficient that decreases from 1 to 0 (sorting the teammates first).
I also feel your model is reasonable, but I would ensure that in those first contests the rating of lone programmers as a group doesn´t change and the same for team programmers, which,if both groups are large enough, is a reasonable assumption.
I once thought about log(exp(rating_a/C) + exp(rating_b/C))*C. We may add D*(sz-1) points to the rating if team size is sz. I suggest C=400 and D=200.
Я думал, окажется, что в одном туристе 228 Бредоров :D
Я правильно понимаю, что регистрироваться в команде из одного участника все равно, что регистрироваться индивидуально?
Да. Если по поводу трансляции Финала VK Cup 2015, то там допускаются командные регистрации только на 2 человека.
Ок, спс