→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 11:08:35 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I guess you like prime numbers, don't you? :P
I mean the rounds that you announce.
Good luck to everyone!
It seems so. Good thing it's the last round otherwise there would be 3 more unannounced rounds!
Let's discuss the problems now. What is the idea behind the 5-th task? I used the O(N^2) in case N<=7000. Otherwise, I do this 2^20 times:
1) Take a random L: K<=L<=N
2) Take a random F: F+L-1<=N
3) T=F+L-1
4) Take the average for the interval [F,T] and compare it to the answer...
Update: WTF?! It got full score :D
I write it using answers binary search,in O(n*log^2 n) ,but it failed,may be it's may mistake in code not in idea (((
Binary-search the answer, rewrite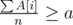 as
as 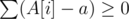 and use prefix sums + 2 pointers on A[i] - a to check if a is a possible answer.
and use prefix sums + 2 pointers on A[i] - a to check if a is a possible answer.
haha I got in correct solution 28,and he got in random solution 140 WTF -_-
There is a justice — I failed A and D :D
hate COCI-s system!!! viva CodeForce!
I was the author of this problem and I apologize, I tried to make test data to break as many bad solutions as possible but it didn't even occur to me that such random solution would find good answers.
Intended solution was, as Xellos already said, binary search the answer P, subtract P from all elements and check if there exists non-negative sum subsequence of length at least K.
Thanks, ikatanic, Xellos and LashaBukhnikashvili for the explanation :)
PS: It didn't even occur to me too that it would pass all tests, I expected only 42 points :D
sorry but did you announce that your problem is a common problem of binary search? link
I haven't tried googling it, it surely isn't standard problem for HONI competitors. HONI is intended for Croatian high school trainings and no one got full score on it. As for COCI (which is open-to-everyone HONI mirror) I thought it would be totally fine (maybe it should have been worth less points) because neither I nor other problem setters have seen this (or similar) problem before.
Also something like convex hull trick and ternary search works.
Could you explain this solution with details?
We map every array element to some coordinates like in the following code:
Now the average can be seen as the slope between two points. Then we iterate through the vector v and maintain a set of points that form the convex hull of the points that we have visited.
Now consider that we have the (K-1)th (the length of the subsequence must be at least K as stated in the problem) non-visited array element (or the corresponding point). We know that the consecutive subsequence that starts from there must start from some of the already visited array elements (or point). It can be seen that we cannot get the best average (or slope) by selecting some point that does not lay in the convex hull. Therefore we can use ternary search to find the best average (or slope).
It seems that there is also somewhat similar solution but which uses two pointers and therefore is O(n), but I don't know it in details.
EDIT: I hope I'm now a bit easier to undestand...
Nice solution , thank you!
the tip that I learnt from this is that when ever the problem ask you to maximize a function that contain a fraction consider a convex hull solution.
What is the convex hull trick?
See these: http://wcipeg.com/wiki/Convex_hull_trick http://codeforces.me/blog/entry/8219
I'm not sure if my solution can be called a convex hull trick, but at least there is some similarity.
Damn, I managed to write 10^6 with 5 zeroes as upper bound of my binary search, damn :P
How to solve C?
My idea is to consider all permutations of the rows. I mean:
row1
row2
row3
and then
row1
row3
row2
and so on...
Now, let's build a graph for each permutation. From element in row i and column j there is an edge to (i,j+1) with weight a[i][j+1] and to (i+1,j+1) with weight a[i+1][j+1]. Of course, if there are no such positions we will not put edges.
For each permutation run Dijkstra from (1,1). The answer for the current permutation will be in (3,N). At the end, the answer is the minimum of the answers for each permutation.
Code: http://ideone.com/CMXKqJ
Looking at the official solution the problem setter only usude the first permutation (row 1,2 And 3). You know why?
I have absolutely no idea why, my idea seems to be exactly the same but with all 6 permutations. Can someone explain it, please?
simply the official solution code is not correct!
I tried it on the sample test cases
It's because that was HONI version of the task (permutation was specified in the task). COCI solutions are up now so you should check them out.
EDIT: Sorry, actually HONI solution was accidentaly uploaded to COCI, it will be fixed soon.
let see all permutation about this 3 array. first we are picking numbers from first,then from second and then from third: then if you are picking numbers from second array in (l,r) segment, for this ans=sum[1][l]+sum[2][r]-sum[2][l]+sum[3][n]-sum[3][r] (sum[i] its prefix sums in i array).
if we will choose l from 1 to n-2, all will be const except sum2[r]-sum3[r],this means that we need such r,that sum[2][r]-sum[3][r] will as small as possible,you can write preprocessing for it,its all. sorry for my bad english )) here code.
I came up with different N*sqrt N solution for 5th task: If we have an subsequence with average a [L,R], we can add to end of it subsequence [R+1,X] where [R+1,X] has largest average from all subsequences that begin in R+1 and the average is larger than a.(it will increase average of original subsequence). We will do this until there isn´t any subsequence that we can add to end.
To make it faster we will add only subsequences that are larger than sqrt(N), and when there is no subsequence larger than sqrt(n), we will add subsequence smaller than sqrt(N) that will at most increase the average of subsequence.
We can calculate where ends the subsequence larger than sqrt(n) with largest average with similar DP method(from right to left).
Is this solution correct and would it pass?
I am really sorry for my bad english.
Could someone tell if it is correct?
Please I am not sure that i am able to code it so I would be really happy if someone said if it is good idea(and if it is correct it should be in solutions pdf :-))
Last November, There was a task which is almost the same with the 5th one of this COCI at the Turkish National Olympiad In Informatics. Unlikely with the COCI version of this task, Turkish one was required finding the average of the consequtive subsequence whose average is maximum off all the consequtive subsequences whose lengths are between given two integers A and B. The time complexity for this question was O(NlogT). ( T = number range )