I tried to solve problem e in round 199 xenia and tree using heavy light decomposition but I couldn't figure out the whole idea anyone ?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 160 |
| 5 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 151 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 14:40:02 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











EDIT: Wrong idea. As Xellos said: every problem has a simple, clear, obviously incorrect solution :D
thnx for your reply donot u have a link for that solution ?
This problem can be solve easier with centroid decomposition.
what is that "centroid decomposition" ?
Centroid of a tree is a vertex that after deleting it, every component will have at most n/2 vertices. You can easily prove its existence. So, using this, you can use divide and conquer on trees and if your time complexity for each merge(conquer) is O(f(n)), then the total complexity would be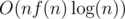 ; Because you did it at most
; Because you did it at most 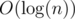 times on each vertex(every time, the size of the component a vertex u is in it would be half of the previous one).
times on each vertex(every time, the size of the component a vertex u is in it would be half of the previous one).
Almost give up, but it works. Handle the segment carefully and not affect other segment values (by limit range update between chain root and chain tail of each chain) https://codeforces.me/contest/342/submission/111296661