determinism's blog

Two Approaches on 2D Segment Trees
By determinism, 10 years ago, In English

I was researching about 2d (multi-dimensional) segment trees. Firstly, I've looked PrinceOfPersia's tutorial, but there wasn't much about 2d segment trees; that's why I've researched a little bit and found this blog.

Even though, PrinceOfPersia's tutorial doesn't tell much about 2d segment tree, it says that every node in main segment tree is also a segment tree. On contrary, other blog describes a totally different idea.

Can someone explain me (or point out a website that explains it) the idea represented in PrinceOfPersia's tutorial and compare (complexity, usages etc.) these two different approaches? Also, it looks like range update with lazy propagation would work with a quad tree. Is lazy propagation possible in other one?

UPD: Thank you really much for good answers! They're really useful.

  • Vote: I like it
  • +12
  • Vote: I do not like it

Comments Comments (8)
| Write comment?
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I think PrinceOfPersia's tutorial about 2d segment tree is same as this tutorial.I think Quad tree is better, it is hard to understand.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    And Quad tree is slow. It works in worst-case O(N) per query.

    → Reply
»
10 years ago, # |
  Vote: I like it +15 Vote: I do not like it

2D Segment tree != Quad tree. PrinceOfPersia's tutorial is indeed about 2D segment tree

→ Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

A quad-tree is much different from a 2D segment tree. However 2D segment trees or interval trees are much more useful in competitive programming (don't generalize).

That blog you mentioned has a very nice and detailed explanation of quad trees, however it is not the same as a 2D segment tree. Check out a nice 2D segment tree implementation here: e-maxx 2D segment tree.

Also, did you know that quad-trees have worst case complexity O(n)? Here is an elaborate explanation: quad-tree complexity

Quad-trees are handy at times, and they certainly feel more natural to grasp and are easier to code in my opinion. But it is better to learn and use 2D segment trees whenever possible.

→ Reply
»
10 years ago, # |
  Vote: I like it +11 Vote: I do not like it

As for lazy propagation in 2D segment tree, I don't think it's possible. However, I think that in some cases it is possible to make a segment tree update values in a rectangle in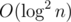 . In particular, this can be done when:

  • The operation  *  the tree does is both commutative and associative.

  • The update we want to do is like this:

    Update(Rect, c): for each element a in rectangle Rect replace a by a * c.

So, for instance, it is possible to write a 2D segment tree that can compute sum of elements in a rectangle in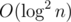 and add a constant to all elements in a rectangle in .

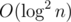DISCLAIMER: I don't know this from any reliable source, it's just an idea I came up with. I may have forgotten some important property, or I might be completely wrong.

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

The link in the blog (this blog) has expired and links to a malicious adult website. determinism, please update or remove the link.

→ Reply