Введем вспомогательное определение. Полупустой квадрат — это такой изначально пустой квадрат, в который положили печеньку максимально возможного размера.
Заметим, что, если добавить в полупустой квадрат размера 2n × 2n печеньку максимального размера (она будет иметь размер 2(n - 1)), то наш квадрат разобьется на 4 квадрата величины 2n - 1 × 2n - 1, три из которых будут полупустыми квадратами, а один будет полностью заполнен. Отсюда следует формула f(n) = 3 * f(n - 1), f(0) = f(1) = 1. Переходя к замкнутой форме, получим ответ 3n - 1 (при n > 0) и 1 (при n = 0).
Задача B.
Очевидно, что предложения следует помещать в SMS жадно. Действительно, если мы можем поместить предложение в текущее сообщение, то нету смысла начинать новое, т.к. при этом количество сообщений может увеличиться. Единственным подводным камнем в задаче была необходимость аккуратно обрабатывать пробелы между предложениями.
Задача C.
Для начала научимся решать более простую задачу: требуется подсчитать количество счастливых билетиков, в которых 1 ≤ a ≤ x и 1 ≤ b ≤ y. Преобразуем выражение a * b = rev(a) * rev(b) к выражению вида a / rev(a) = rev(b) / b. Переберем все возможные a и подсчитаем кол-во обычных несократимых дробей вида a / rev(a) (double, кстати, тоже работает =) ) с помощью какой-нибудь структуры, например, map из STL. Остается для каждого значения b найти количество совпадающих дробей a / rev(a) с rev(b) / b и добавить к ответу.
Теперь перейдем к нашей задаче.
Если счастливых билетов с ограничениями 1 ≤ a ≤ maxx и 1 ≤ b ≤ maxy меньше w, то x и y, удовлетворяющих условию задачи, не существует и следует вывести - 1.
Если решение существует, то воспользуемся методом двух указателей.
Нам потребуется поддерживать количество счастливых билетов 1 ≤ a ≤ x и 1 ≤ b ≤ y. Для этого заведем две структуры типа map (назовем их m1 и m2). Научимся переходить из состояния (x,y) в состояния (x,y+1), (x+1,y), (x,y-1), (x-1,y). Если мы хотим увеличить (уменьшить) значение x, то к значению количества счастливых билетиков мы прибавим (отнимем) m2[x/rev(x)] и увеличим (уменьшим) значение m1[x/rev(x)] на единицу. В случае с изменением y следует выполнить аналогичные действия.
Зафиксируем некоторое состояние (x,y), где x = maxx, а y = 1 и подсчитаем для него количество счастливых билетиков. Будем увеличивать y, пока баланс счастливых билетиков не станет больше или равен w. Очевидно, что это будет такое наименьшее y для x, что в соответствующем диапазоне найдется достаточное количество счастливых билетов. Важно отметить, что в дальнейшем уменьшать y не будет иметь смысла. Прорелаксируем ответ и уменьшим x на единицу. Будем повторять действия, описанные в этом абзаце, пока x больше нуля.
Так как x из ответа лежит в пределах от 1 до maxx и для кадого значения x из этого же диапазона мы нашли оптимальное значение y, то в результате работы алгоритма был просмотрен ответ с наименьшим значением x * y.
Так как каждый указатель не принимает одно значение дважды, и время, затрачиваемое на поддержку баланса, порядка логарифма, то общее время работы программы имеет асимптотику O(maxx * log(maxy) + maxy * log(maxx)).
Задача D.
Заметим что любая точка, лежащая внитри треугольника из первых трех точек, будет всегда содержаться внутри выпуклой оболочки в дальнейшем. Зафиксируем одну из таких точек и перенесем центр координат в нее. Будем хранить точки выпуклой оболочки в структуре типа map, где ключом будет угол для вектора из начала координат к какой-либо точке. Каждому углу будет соответствовать одна точка.
Научимся отвечать на запросы второго типа. Для точки в запросе (A) найдем ближайшую точку к ней по часовой (B) и ближайшую против часовой (C) стрелки. Если угол, образованный векторами AB и AC отрицательный, то точка лежит вне выпуклой оболочки, в противном случае точка лежит внутри или на границе.
Теперь научимся обрабатывать запросы первого типа. Если точка из запроса (C) лежит внутри выпуклой оболочки, то ничего делать не надо. Найдем две ближайшие точки по часовой стрелке (ближнюю из них обозначим A, другую B). Если поворот от вектора AB к вектору AC положительный, то закончим обработку точек по часовой стрелке, иначе удалим из структуры точку A и повторим эти же действия. Подобным образом следует обработать точки, лежащие против часовой стрелки относительно C.
Каждая точка добавляется максимум один раз и удаляется максимум один раз. Каждая из этих операций выполняется за O(log(h)), где h — количество точек в выпуклой оболочке. Итоговая асимптотика O(q * log(h)).
Задача E.
Заметим следующие факты. Пусть у нас есть зафиксированное состояние некоторого количества областных центров, тогда для каждой вершины не являющейся, областным центром следует выбрать ближайший к ней областной центр, т.к. d[i] < = d[i + 1]. Утверждается что все вершины лежащие между некоторой вершиной x и ее центром g будут принадлежать этому центру g. Предположим что это не так, тогда g является не самым ближайшим центром для некоторой вершины между x и g, и для нее существует более ближайший центр u, но тогда должно быть dist[x][u] < dist[x][g], что приводит нас к противоречию. Таким образом получаем, что наше дерево должно быть разбито на некоторое количество поддеревьев и в каждом поддереве будет один областной центр. Для общности так же положим d[0] = 0.
Будем решать задачу используя "перекрестное" ДП.
Первая функция DP. D1(T, g, x, s) будет отвечать за формирование поддерева с областным центром g. T -- некоторое поддерево исходного дерева определяемое направленным ребром uv. областной центр g должен содержаться в T. Будем считать что городу v назначен областной центр g. Так я упомянул выше эта функция будет отвечать за формирование дерева с цетром g. Вся задача будет заключаться в выборе тех ребер которые будут ограничивать наше поддерево. Рисунок:
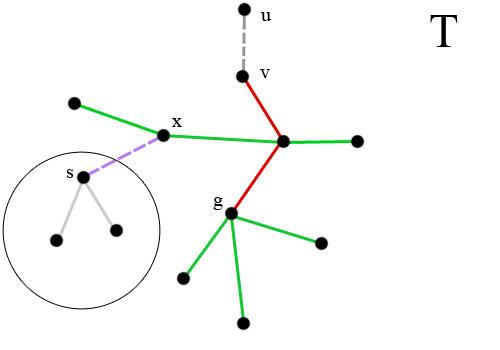
Зеленые и красные ребра соединяют вершины, которым назначен областной центр g. Фиолетовое ребро ограничивает множество вершин, которым назначен центр g. Стоит отметить, что вершины лежащие на пути из красных ребер нельзя использовать как ограницивающие т.к. вершине v уже назначен центр g.
Пусть ребро xs является ограничивающим, тогда для поддерева T' (Вершины этого поддерева обведены в круг) вызовем функцию функцию ДП D2(T').
Вторая функция ДП будет перебирать каждую вершину в поддерве T' в качестве областного центра и вызывать D1.
В первой функции ДП имеется порядка O(n3) состояний т.к. поддеревьев T порядка O(n), вариантов выбора g столько же и пара (x;s) образует ребро, а ребер всего 2*n-2. Вторая функция ДП имеет O(v) состояний и переход выполняется за O(v). Таким образом решение требует O(n3) памяти и имеет асимптотику O(n3).











Может, так?
Перебираем x от 1 до maxx. А y будем искать бинпоиском. Для этого нам бы надо знать массив a[1..maxy] - т.е. a[i] - каков будет ответ, если мы возьмём y=i (понятно, что в терминах задачи a[i] - количество хороших серий для данного билета). Подбирая минимальное y бинпоиском, мы ищем такой префикс массива a, на котором сумма будет >=w. А переходя от x к x+1, мы должны увеличить значения в некоторых ячейках массива (в тех билетах, которые сочетаются с серией x+1). В общем, две стандартные операции на дереве Фенвика - сумма на префиксе и изменение значения.
Ну известно, что Фенвик имеет очень быстрый логарифм, так что ничего удивительного. Да и бинпоиск только штук 17 итераций сделает. Итого где-то 10^5 * 17*20 - т.е. около 40 млн., что весьма мало.
Но я не писал, это только предположения
В E у меня решение за квадрат (наверное, как и у многих - судя по временам работы).
Пусть d[v][p] - ответ для поддерева с корнем в вершине v, если ближайший сверху областной центр находится на расстоянии p. Тогда у нас могут быть такие варианты:
а) мы ставим в d[v][p] областной центр, тем самым переходя за стоимость k в состояние d[v][0]
б) мы не ставим в d[v][p] областной центр, и все областные центры в наших потомках находятся на расстоянии p или более - тогда сыновья являются независимыми, и мы просто суммируем d[child][p+1]
в) мы не ставим в d[v][p] областной центр, но среди потомков есть областной центр на некотором расстоянии q<p - тогда выходит, что этот сын будет влиять на всех остальных, т.е. фактически для остальных сыновей всё будет получаться, как будто бы мы пришли в вершину v с расстоянием q. Чтобы посчитать значение по переходу этого вида, мы перебираем q и сына, в поддереве которого это q находится, и от этого сына запускаем вторую динамику (d2[v][q] - это ответ, если на расстоянии <=q от v обязан быть областной центр), а от всех остальных сыновей и самой вершины v - ответ считаем как в переходе б), как если бы в вершину v мы пришли с расстоянием q.
Весь переход в), чтобы он быстро делался, можно оформить как третью динамику d3[v][q] - она пробует делать третий переход для q, а ещё берёт ответ из d3[v][q-1]. Ну а как делать за O(deg[v]) переход при фиксированном q, наверное, понятно (стандартный приём, что посчитаем сначала сумму нужных величин по всем сыновьям, а затем при переборе выбираемого сына будем выкидывать из этой суммы одно слагаемое).
Вот, выглядит наверное жестковато, но мне как-то было просто рассуждать вот так, поэтапно. Уверен, что эту же идею можно было оформить и без трёх динамик :)
Sorry, I dont really understand the analysis and have a few questions. Hope that you can help me out. Thanks!
Problem D:
May I know why the first three points of the input will definitely be in the convex hull? Is such an input impossible?
1 1 0
1 0 0
1 0 1
1 -1 2
1 2 -1
1 -1 -1
In such an input, the convex hull will be (-1,2) (-1,-1) (2,-1).
Also, for the queries B and C, how do you find the nearest point anti-clockwise and clockwise? Which line of reference do you take to determine whether a point is clockwise or anti-clockwise? And may I know how do you find the nearest point efficiently?
Problem E:
I am not too sure about the DP state definition :(.
I think that what you are saying that first, you root the tree. Then, suppose the edge uv is bounding. Then you are going to get a subtree T, which is bounded by the edge uv. In this subtree, you choose g as the regional centre. Then you try each edge and try to set it as a bounding edge for the next subtree. Suppose you have chosen the edge xs. Then you recursively work on this new subtree. You call DP 2 to bruteforce which vertex should be regional centre be located at. Then you call DP 1 again. So say you call the next subtree T' and the node you are building regional centre p. Then you will call DP1 (T', p, x, s).
Is this what you are saying? Please correct me if I am wrong.
Also, may I know how do you represent a subtree in your DP state? And it seems to me that given any tree, there are a lot more than N different subtrees (for example, given a line graph I think there are about N^2 different subtrees. There are about N^2 different sets of endpoints you can choose from, and each set defines a unique subtree). Am I missing something here?
Sorry, I am new to this kind of DP, so my questions might sound a bit obvious XD. Thanks a lot!
Sorry, posted message in the wrong place: http://codeforces.me/blog/entry/1598#comment-30470
D.
UPD: any point from the triangle based on first three points will be into the area bounded with the convex hull in the future.
To find the nearest point efficiently use binary search tree (if you write in C++ you can use map class).
E.
Yes, you understood what I mean. You should recursively bruteforce xs edge. T is represented in next way: edge uv divides tree into two subtrees, T is one of these subtrees containing vertex v.
Thanks for your reply! I think I understand how to do problem D now.
But I am still not too sure about problem E. I dont quite understand the function DP 2. What does it store? Does DP 2[x] store the min cost if you build a regional centre at x? But won't the answer be different if your subtree is different? What is the recursion for DP 2 like?
Thanks in advance again!
I have finally understood how this works. Thanks! =D
Is it possible for you to look at this problem and give me your thoughts? It does sound very similar. Thanks in advance! http://codeforces.me/blog/entry/1621