AkshajK's blog

Topcoder SRM 647
By AkshajK, 10 years ago, In English

Topcoder SRM 647 will be held tomorrow (Saturday) at 12:00 Noon EST; details here. Discuss the problems here after the contest!

  • Vote: I like it
  • +38
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

a very similar problem to div1 500 discussed here

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve 1000? I get that it's some kind of modified mincut, but...

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    I did it this way.

    1. Let's find all strongly connected components. If the start and the end vertex are in the same component, the answer is -1.

    2. Now we can build a graph where the vertices are strongly connected components and there are all edges from the original graph(except those that lie inside the same component, of course).

    3. If there wasn't an additional condition that we can block only one edge on each path, we could have just found the minimum cut in the graph. But we can adjust the graph in such a way that this condition is satisfied. That is, for each pair of edges (A -> B) and (X -> Y), we should add an edge from X to B with cost = INF if and only if A is reachable from the start vertex, the end vertex is reachable from Y and X is reachable from B.

    4. The minimum cut(or the maximum flow) in this graph is the answer(if it is < INF, otherwise the answer is -1).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I probably should've specified what I know better than "modified mincut", since I only needed point 3 :D

      but nice one.

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      It's enough to add all inversed edges with cost INF, and then find mincut.

      But you should remove vertices, which are not on paths from 1 to n. I lost this.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        How can you proof this works? At least what is the idea?

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Consider a node v which lies on some path from S to T. One can prove that either 1) there is exactly one marked road on any path from S to v, or 2) exactly one marked road on any path from v to T. And if you know what is the case for each node, then you need to mark every road leading from a node of type 1 to a node of type 2. Also, roads mustn't lead from a node of type 2 to a node of type 1.

          And you just find the optimal partition using mincut.

          → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          If you have 2 cut edges a->b and c->d on a path 0--->a->b--->c->d--->(N-1), the only case where you can't just remove one of them from the cut to make a smaller valid cut is when there's a path from vertex 0 to some vertex on the path b--->c and another path from an earlier (in DAG ordering) vertex on b--->c to N - 1.

          If we add an edge c->b that can't be cut, it would stop being a valid cut.

          → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    You can't block any edge of a SCC (because cycles), so join all SCCs into a single vertex, and add costs for every edge between SCCs to get new costs.

    Now we still have to enforce "can't go through two blocks" condition. To do this, for every edge in the forward direction, make an edge in the reverse direction with infinite capacity.

    And please remember to delete all SCCs that aren't part of any 0 to N-1 path before the mincut, otherwise the troll test will hunt you at night.

    → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

  1. For each building compute its maximum possible height. For each constraint t[i] on x[i] it gives t[i] + |x[i] - j| constraint on j. The answer is maximum over the computed heights.

  2. If we have robots a0 ≥ a1 ≥ ... ≥ ak then we can reach distance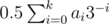 . We use simple dp[budget][prefix] to compute best value.

  3. I thought it was scc and then flow. But many solutions fails. So there are some tricky cases...

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you provide the explanation for 2nd problem?, please

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      First part is to get this formula for best reachable distance. Just solve it for 2,3 robots and then some induction argument.

      For 2 robots a ≥ b the answer is 0.5(a + b / 3). 2nd robot should turn around in the first moment s such that no fuel will be lost. So first robot should have b - 2s place in his tank (for fuel which is useless for b), so s = b - 2s and s = b / 3.

      If we have more robots then we can compute moments in which they have to turn around in the same way. i.e. Each robot should turn around in the first moment such that no fuel will be lost (next robot has already place for useless fuel of actual robot).

      After careful computations we get the formula 0.5(a0 + a1 / 3 + a2 / 9 + ...).

      The second part is standard dp. We sort robots by increasing capacity. For each prefix of robots k and budget b we compute dp[b][k] which is best distance if we can use only k-first robots and have b dollars. The transition formula is

      dp[b][k] = max(dp[b][k - 1], 0.5ak + dp[b - cost[k]][k - 1] / 3).

      We can take k-th robot or not.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I couldn't understand div1-500. In the sample test #0, why 2 robots with capacity 1 must stop at 1/3 first? They can stop at very close 0 point, then robot 1 can donate amount of fuel to robot 2 more than when they stop at 1/3. Hence, the largest distance robot 2 can go will as far as possible.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    The amount of fuel a robot can contain is limited by its capacity

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain how to solve the div-1 500?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Sort the robots by their capacity in increasing order , then apply this dp:

    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cost[i]] / 3 + cap[i])

    then the final answer is max(dp[n - 1][i]) / 2

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am interested to know about solving Div 2 1000, I got binary search as the only idea which gives wrong answer. Any better ideas?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Betlista wrote a short editorial for Div 2 here. You can see a more detailed discussion for the 1000 problem in the comments.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone please comment on this? I have a problem with understanding what is wrong with my solution:

http://codeforces.me/blog/entry/16046

→ Reply