I am trying to solve this problem on spoj. The problem gives an input of n integers and then asks q queries which are of the form l r k and the program has to output number of elements greater than k in the subsequence al, al+1, ..., ar. I am using persistent segment trees to process queries online.but i am getting wrong answer. I am not able to find why my code fails.
Here's my code
Note: I know there's a way to solve this problem offline.But I am interested in online solution.
You can solve this problem in online without persistent data structure but it will be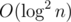
per query...
Anyway your solution is offline because you compress input (btw you don't need to do it if you maintain tree with pointers).
Also here you can query sor[0], but looks like it's uninitialized
Also doesn't ind should be a power of two? Oo
Thank you for your time.
I think you are talking about using a merge sort tree, I tried using that but it exceeds time limit.
Also, I am finding rank of k in array and to do that I am assigning it the rank of the last element that is not greater than k in the array, I think that makes sense. Lets say the arr[] is 7 5 9 3 12 and query is 1 3 2.
sor[] is: 3 5 7 9 12
pos would be 1, pos-1=0, sor[0] would be 0, so m1[0] would be 0 (as 1<=ai<=10^9) So new k would be 0, and task reduces to finding numbers greater than 0 in {3,2,4} which would be 3,the answer as expected.
Anyway to be more sure that sor[0] doesn't contain garbage, I initialised it to 0 and m1[0] to 0, still wrong answer.
I don't see where it could fail, maybe you could help me out with a test case.
And I don't get your last point at all, why should ind be a power of 2?
Also I would appreciate if you could tell me about that approach using pointers and avoiding compression.
When you use pointers you create no more than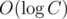
new elements on each query, where C is the maximum element in the array. So you can don't care about compression at all and solve the problem in 
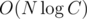if you know the maximum element (or upper bound for it as 109 in this task).
I actually don't know... I thought so earlier...
Btw you can try to solve this problem with persistent bit trie (which is actually equivalent to segment tree) as described here.
That's right.That's what I did earlier but since time limit is strict, without coordinate compression query would be O(log(10^9)) which times out.That's why I used compression to reduce query to O(log(3*10^4)) but now it gives wrong answer. Actually, solving the problem is not my concern.Problem can be solved using a lot of data structures including fenwick tree.I want to know limitations of my program. As a matter of fact, I am getting wrong answer for 2 more questions that I tried solving using persistent segment trees.I don't know where's it all going wrong..
problem
Here's the code.
Strange. Similar problem, your code gets accepted.
First of all, don't use pointers. They make your code really unclear to me and almost impossible to debug. Persistent segment tree can be written really nice and clean. I've just solved this problems few days ago.
Here's my solution: http://ideone.com/OC64oc
You're right — it gets TLE, because lower_bound in O(log(109}) per query. But you can sort queries and find right root vertex of a tree in amortized O(1).
http://ideone.com/j0N7lB
This solution got AC in 0.44s
Well, the fact that pointers make this code unclear for you means only that you're not familiar with them.