Hello,
I'm struggling with following problem: We have n < 37 cities and m < n * (n - 1) / 2 undirected roads between them. Every city has a treasure in it with g[i] gold. Our robbers wants to get from city 0 to city n - 1 and take as much gold as they can with them.
To do this, they can (or not) rob every city they visit. They're hurry, so they can visit only cities that land on the shortest path from city 0 to n - 1 (if there are more than one shortest path, they can choose freely).
But there is a catch — they also need to go back from city n - 1 to 0 (now, they can move as they want), but! they cannot visit any city they robbed twice (dwellers will wait for them).
How much gold can they rob on they way to city n - 1?











Should they follow a shortest path and do they rob the cities on their way-back?
They don't need to follow shortest path on their way home and they cannot rob anything. I updated the statement.
Then can't you generate all paths between 0 and n-1 and choose each two non-intersecting paths? I'm not sure about the complexity but the constraints are very little.
I'm getting TLE. My solution: http://ideone.com/8VYi2L
Okay, try to do this:
1) Present the graph by matrix of adjacency.
2) Find the length of the shortest path from 0 to n-1.
3) Generate all paths from 0 to N-1 with that length;
4) For each path remove the edges that come from the used nodes(except 0 and n-1) Then run DFS/BFS from n-1 If you can reach 0 this is a correct path, find the amount of gold if you follow it and actualize the answer. Then restore the removed edges.
I think that's what I did above. Attention: In original statement (and in my code) vertexes are 1-indexed, starting vertex has a number 1 and ending has a number 2
Oh, I'm sorry, I started writing the comment before you put your code here. Hope someone will explain a faster solution.
Please, provide a link to the problem at an online judge.
It's on the internal site of my University.
OK.
I have breafly read your code and think that it can consider one way multiple times.
For instance, on this input your code has been working for a long time while there is only 211 ways from 0 to 1.
I think this was from NAIPC 2014. http://serjudging.vanb.org/wp-content/uploads/NAIPC-2014-Problems.pdf (Problem F)
Here's how to do it. First you can generate all shortest paths, since there will be at most 2^(n/2) of them, which is 2^18, which should run in time. Now, let's say you take gold from every city. Then, now, you want to find the shortest path from node n-1 to node 0, where if we travel on a node, and it is part of the shortest path, we will remove it from our total cost. Here is a sample solution: http://serjudging.vanb.org/wp-content/uploads/Gold_Calvin.java
I want to add that original testcases are weak — this problemset was also used for Opencup — GP of America, and as i already mentioned in russian discussion of that GP, my AC solution from a contest uses almost naive backtrack, and it wasn't able to solve one of my custom tests even in 45 minutes :)
hahahahahahahahahahahahahahahhahahahaha
Can you send me this custom test? I want to see if it breaks other backtracking solutions. I was sad to see backtracking pass when the intended solution was more beautiful.
It was also sad to see a few greedy solutions pass on this problem in contest. :(
Why?
Because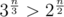 , that's why :P
, that's why :P
Why 3n / 3. Where did you get that number from?
Split graph into N / 3 buckets. Then add 3 edges from each node. This edges will go to next bucket's 3 nodes. If each edge have equal weight then number of shortest paths equals 3N / 3 and shortest path length is N / 3.
I guess if we split graph into N / e parts we can get more shortest paths :)
You can bound the run-time using dynamic programming. The maximum number of paths in a level graph is equal to the maximum product of positive integers that sum to the number of nodes. We assume that between each layer is fully connected. A path simply chooses one node for each layer.
Write the dp for N=36 and you will see it is not very big. (Do a trace back to find the exact composition)
The intended solution was to find all possible shortest paths and then use O(V^2) Dijkstra's to payback the cost. A rough estimate of this bound is O(2^(N/2)*V^2) but it is not exact.
No need for the DP. You obviously don't want a layer with 1 node, it's better to add that 1 node to another layer. You don't want any layer with 4 or more nodes, because you can always split a layer with k>=4 nodes into a layer with 2 and a layer with k-2 nodes and the number of paths doesn't decrease. And you want at most two layers with 2 nodes because 2 layers with 3 nodes each are better than 3 layers with 2 nodes each (3*3=9 and 2*2*2=8 which is less). This uniquely determines the multiset of layer sizes.
My friend JohnPaulII told me this problem recently. I told him one solution I came up with (some kind of backtrack), but he insisted that this will receive TLE, so we made a bet. We agreed that I can have at most 2 TLEs before getting AC to win a bet. I coded one solution and sent it to him. Then I went sleep and when I woke up I realized that in fact my solution is pretty slow and thought that I should tell him that he shouldn't sent my solution, because that will get TLE. But he has sent it before I told him not to do so and it got AC :P. In fact original testcases must have been pretty weak.
Here is my code, simple backtrack: http://ideone.com/sHRqqQ
I know that this is pretty easy to create testcase so that this will TLE, but I remember that there was an optimization such that I didn't know bad testcase for it, but also I didn't know proof why it is running quickly (and don't remember this optimization now, but it was pretty natural).