Есть массив чисел. Как быстро отвечать на запросы
- прибавить число на отрезке
- узнать сколько раз число встречается на отрезке?
Пока что ничего быстрее  не придумал.
не придумал.
Если кому интересно, идея sqrt-декомпозиции:
- разобьем массив на
 блоков
блоков - для каждого блока будем хранить
- cnt[x] — количество чисел x в блоке
- delta — число, которое надо прибавить ко всем числам в этом блоке
Тогда на запрос прибавления числа D на отрезке будем отвечать так:
- Если блок полностью входит в отрезок, то изменим его delta на D
Иначе пройдемся по элементам, которые лежат в границах запроса, и просто добавим к ним D
cnt[a[i]] --; a[i] += D; cnt[a[i]] ++;
Запрос о количестве чисел X на отрезке:
- Если блок полностью входит в отрезок, просто вернем cnt[X - delta]
- Среди остальных элементов учтем те, которые равны X - delta











За O(log2(n)) вроде можно. Будем поддерживать дерево отрезков, в котором будем хранить количество каждого числа, которое входит в отрезок в мэпе и значение delta. Ответ находить ровно так же, как при корневой декомпозиции для полных блоков. Запрос на добавление — просто в дереве отрезков для нужных вершин увеличиваем delta.
p.s. не прочитал в тэгах, что ты хотел log(n) на запрос)
Не обязательно O(log(n)), хотя бы что-нибудь быстрее корня (:
Как тогда мержить сыновей вершины с разными delta? Например, такие запросы:
По идее, нужно взять ответ из корня, не спускаясь вниз. Как это сделать?
Я попытался на скорую руку написать структурку. Вот что получилось.
Так у вас update работает за O(количества чисел в поддереве), так что inc будет работать как минимум за O(длина интервала).
Да, действительно. Был неправ.
Ну круто, всегда удивлялся среднестатистическому пользователю кодфорс. Не раз встречал комментарии, неуместные по тем, или иным причинам. В этот раз автором этого комментария стал я. Этот пост(как и мой комментарий) прочитало не мало человек, из них почти все подумали что-то типа : "комментатор рак, дебил, поставлю ему минус(от которого никому лучше не станет), он его заслужил" и лишь один(!), спасибо ilyakor, объяснил, в чем моя ошибка. Супер. Класс.
Ой, все.
тут очень странно людей заминусовывают ) не удивлюсь если и с твоим новым комментарием так же поступят, их уже не остановить =)
Недавно обсуждали похожую задачу, в тот раз дальше всем известного решения с корневой не продвинулись.
Вроде делается быстрее чем за , правда, я сомневаюсь, что это очень практично.
, правда, я сомневаюсь, что это очень практично.
Делаем дерево интервалов, у которого в вершинах лежат Rope'ы, умеющие отвечать на запрос "сколько в тебе чисел x" и прибавлять константу ко всему Rope'у. Запросы делаются тривиально, а вот обновления довольно хитрые. В процессе обновления надо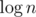 раз cmerge'ить левый и правый Rope'ы в каких-то вершинках. Копировать мы их при этом не хотим (т.к. это долго), а хотим merge'ить за log n без копирования. Это можно сделать, если у нас есть персистентность.
раз cmerge'ить левый и правый Rope'ы в каких-то вершинках. Копировать мы их при этом не хотим (т.к. это долго), а хотим merge'ить за log n без копирования. Это можно сделать, если у нас есть персистентность.
Только я очень сильно сомневаюсь, что это будет работать быстрее корневой оптимизации на тестах вменяемого размера.
Жесть с:
Ладно, если что, буду писать корневую (:
А разве мы должны merge'ить ? Мы же не хотим просто приписать в конец одного массива другой. По-моему, нам придется их объединять. А объединение это медленная операция. Если использовать не Rope а Декартово дерево, то будет выполняется за M log(N/M).
Ну да, нужен не Rope, а обычное декартово дерево. И объединение будет тормозить. Значит, так просто не сделаешь, жаль :(