Всем привет!
В этот раз я хотел бы написать про алгоритм Ахо-Корасик. Структура эта очень хорошо описана и многие о ней уже, должно быть, знают. Однако, я всё же постараюсь описать некоторые применения, которые не столь известны.
Для начала о самой структуре. Данный алгоритм был предложен Альфредом Ахо и Маргарет Корасик. Изначальное его предназначение — оптимальный поиск строк из какого-то набора в тексте. Т. е., допустим нам даны строки {"a", "abba", "acb"} и дан текст, скажем, "abacabba". С помощью Ахо-Корасик мы сможем для каждой строки из набора сказать, входит ли она в текст и, например, указать первое вхождение в строку за время 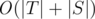 , где |T| — суммарная длина текста, а |S| — суммарная длина шаблонов. Но на самом деле это капля в море по сравнению с тем, что позволяет делать этот алгоритм.
, где |T| — суммарная длина текста, а |S| — суммарная длина шаблонов. Но на самом деле это капля в море по сравнению с тем, что позволяет делать этот алгоритм.
Чтобы понять, как все это следует делать — обратимся к префикс-функции и алгоритму КМП. Напомню, префикс-функцией называется массив π[i] = max(k): s[0..k) = s(i - k..i], то есть, π[i] — длина наибольшего собственного (не совпадающего со всей строкой) суффикса, который совпадает с префиксом для подстроки [0..i]. Рассмотрим простейший алгоритм её получения. Пусть у нас уже посчитаны все значения префикс-функции на отрезке от 0 до i - 1. В таком случае мы можем несколько раз "попрыгать" по позициями π[i - 1], π[π[i - 1] - 1], π[π[π[i - 1] - 1] - 1]... и так далее. Пускай в данный момент после ряда прыжков мы находимся в позиции t. Если s[t + 1] = s[i] и при этом t максимально возможное, то тогда и только тогда π[i] = t + 1. Если считать префикс-функцию описанным выше способом, мы получим её за 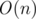 . Действительно, на каждом шагу мы несколько раз сужаем область поиска, а в конце расширяем её всего лишь на один элемент. Расширений будет не больше n, а сужений, очевидно, не может быть больше, чем расширений. Однако, в процессе пересчёта префикс функции для конкретного индекса мы можем честно пройти все i - 1 символов до него, что может сильно усложнить жизнь в некоторых случаях.
. Действительно, на каждом шагу мы несколько раз сужаем область поиска, а в конце расширяем её всего лишь на один элемент. Расширений будет не больше n, а сужений, очевидно, не может быть больше, чем расширений. Однако, в процессе пересчёта префикс функции для конкретного индекса мы можем честно пройти все i - 1 символов до него, что может сильно усложнить жизнь в некоторых случаях.
Позже будет показано, как улучшить оценку подсчёта в отдельно взятой позиции до строгой  . Пока же давайте построим автомат[1], который позволит нам знать, чему равна длина наибольшего суффикса некоторого текста T, равного префиксу строки S и кроме этого добавлять символы к концу текста, быстро пересчитывая эту информацию. Итак, пытаемся "скормить" текст автомату, т.е., пройти по символам в автомате, которые соответствуют строке. Если нам это удаётся, то всё хорошо. Иначе же мы переходим по суффиксной ссылке, пока не обнаружим требуемый переход и продолжаем. Суффиксной ссылкой здесь и далее будем называть некий указатель на состояние, соответствующему самому длинному собственному суффиксу строк, которые принимает текущее состояние (т.е., пройдя по символам которых мы попадём в состояние), который имеет собственное состояние. Легко видеть, что в данном автомате суффиксной ссылкой будем выступать значение префикс-функции. И вновь мы можем за
. Пока же давайте построим автомат[1], который позволит нам знать, чему равна длина наибольшего суффикса некоторого текста T, равного префиксу строки S и кроме этого добавлять символы к концу текста, быстро пересчитывая эту информацию. Итак, пытаемся "скормить" текст автомату, т.е., пройти по символам в автомате, которые соответствуют строке. Если нам это удаётся, то всё хорошо. Иначе же мы переходим по суффиксной ссылке, пока не обнаружим требуемый переход и продолжаем. Суффиксной ссылкой здесь и далее будем называть некий указатель на состояние, соответствующему самому длинному собственному суффиксу строк, которые принимает текущее состояние (т.е., пройдя по символам которых мы попадём в состояние), который имеет собственное состояние. Легко видеть, что в данном автомате суффиксной ссылкой будем выступать значение префикс-функции. И вновь мы можем за 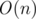 целиком пропустить строку через автомат из тех же соображений, которые были указаны в прошлом абзаце.
целиком пропустить строку через автомат из тех же соображений, которые были указаны в прошлом абзаце.
Посмотрим теперь, как улучшить до константы время одного такого перехода. Давайте сделаем автомат полным, т.е., чтобы из каждого состояния были переходы по каждой букве из алфавита. Тогда, очевидно, переход будет требовать всего одно действие. Но как это сделать? Очень просто! Допустим, у нас посчитаны переходы в автомате для всех k < i. Легко заметить, что всё, что нам нужно, чтобы получить корректные переходы из состояние i — скопировать их из состояния, в которое мы бы перешли по суфф ссылке и затем заменить один единственный переход — по букве s[i + 1] в состояние i + 1. Суфф ссылку же для этого состояния можно получить, перейдя по символу s[i] из суффиксной ссылки состояние i - 1. Как можно видеть, всё считается за  . Или, что точнее — за
. Или, что точнее — за 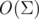 , где
, где 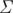 — размер алфавита.
— размер алфавита.
Наконец, вернёмся к задаче о поиске нескольких строк. Кому-то может показаться, что это только начало долгого и нудного описания алгоритма, но на самом деле алгоритм уже описан и если вам понятно всё, что изложено выше, вы поймёте и то, что я напишу сейчас.
Итак, обобщим автомат, полученный ранее (назовём его префикс-автомат). Объединим наш набор строк-шаблонов в префиксное дерево. Теперь сделаем из него автомат — в каждой вершине бора будет храниться суффиксная ссылка на состояние, соответствующее наибольшему суффиксу строки данной вершины, который присутствует в дереве. Можно видеть, что абсолютно аналогично тому, как это делается в префикс-автомате мы теперь, пропуская текст через новый автомат, в любой момент можем поддерживать состояние, которое соответствует наибольшему суффиксу пропускаемой строки. Осталось только научиться считать эти ссылки.
Я предлагаю делать это таким образом: запустить обход в ширину из корня. Пусть в данный момент мы находимся в состоянии v. Тогда "протолкнём" суффиксные ссылки всем его потомкам в боре по тому же принципу, как это делается в префикс-автомате. Такое решение корректно, т.к. если мы находимся в вершине v при обходе в ширину, у нас уже посчитан ответ для всех вершин, расстояние которых до корня (т.е. длина соответствующих им подстрок) меньше, чем у нашей, а именно такое требование мы раньше предъявляли при получении суфф ссылок в префикс-автомате. Есть также некоторые другие способы, использующие "ленивую" динамику, их можно видеть, например, на e-maxx.ru.
[1] В данном случае будем считать автоматом некий ориентированный граф, над дугами которого написаны символы. Вершины в нём будем называть состояниями, а дуги — переходами. Пройдя какой-то путь по этому графу, мы окажемся в состоянии, которое соответствует строке, которую мы бы получили, если бы записывали символы, по которым мы "переходили". Это не совсем корректно, но такого определения достаточно для того, что мы собираемся делать. В данном случае автоматом будет сама строка. Таким образом, из состояния i будет переход по букве s[i + 1] в состояние i + 1.
Реализация основных функций: http://ideone.com/J1XjX6
Альтернативная версия: http://ideone.com/0cMjZJ
Легко проглядывается схожесть с префикс-функцией.
Рекомендуемые задачи:
- UVA — I love strings!!
- Timus 1269 — Антимат
- Timus 1158 — Censored!
- MIPT El Judge — Вопль
- SPOJ — Morse
Позже я хотел бы рассказать о некоторых более продвинутых трюках с этой структурой, а также об одной интересной родственной структуре. Так что stay tuned :)
P.S. Если вам что-то непонятно или кажется слишком сложно описанным, хотя можно было бы легче — пожалуйста, не стесняйтесь написать об этом в комментариях. Я стараюсь сделать статью максимально понятной, но я не могу гарантировать, что мне это всегда удаётся :)











Примерно месяц назад я писал разбор некоторых задач на эту тему для младших поколений асм-щиков в нашем универе. Если кому-то интересно — вот он. Если возникают вопросы — пишите здесь или там в комментах
а также об одной интересной родственной структуре
Надеюсь, речь идёт не о дереве палиндромов? :)
Timus 2040
Устал от него, пока готовил?)
От дерева или от Рубинчика? Хотя скорее от палиндромов вообще устал :)
Вот придумали вы это ваше дерево палиндромов, а дальше что? IRL ему нет применения, олимпиады по программированию — единственная область, где оно нужно, зато теперь поколения ACM-щиков будут проклинать вас, увидев контесты, подобные последнему контесту на тимусе (полагаю, он уже получил такие отзывы)
А что не так с тем контестом? Задач на дерево палиндромов там было всего две, что вроде бы вполне нормально для контеста, где структура была представлена впервые.
Что дальше, предложишь вообще не делать задач, решение которых имеет мало общего с IRL? Ну таким образом от очень большого слоя задач избавимся. Я вот, например, с трудом представляю ситуацию, когда мне дарят на День Рождения массив и я бегу писать программу, чтобы узнать, как его можно обработать. Зато с такой логикой можно будет с чистой совестью давать какие-нибудь задачи типа "уложите граф на плоскости за O(n)".
вот зря Вы так. во-первых, задачи на палиндромы и до этого были, но решались на порядок сложнее (даже Манакер (при всей своей простоте) пишется сложнее, чем дерево палиндромов без наворотов, а функциональности у последнего больше). во-вторых, математике уже известны вещи, которые создавались ради интереса / забавы без практической пользы, а потом вырастали в мощный аппарат (насколько мне известно, те же комплексные числа). в-третьих, почему бы нам, как олимпиадникам, не порадоваться за еще один новый подход к решению задач? ;-)
Одно дело — порадоваться за клевый подход к решению задач. Другое дело — "рекламировать" это везде и всюду, практически заставляя изучать эту структуру.
А, я понял, почему меня в ветке opencup'a минусовали :)
Никто не хочет, чтоб кто-то знал об этой структуре, потому что иначе прийдётся её изучать, чтоб не быть где-то внизу таблицы, когда очередной Рубинчик даст задачу на палиндромы)
"Придется ее изучать" звучало так, как будто там 100 страниц сложнейших конструкций.
Никто не говорит, что палиндромное дерево — это что-то плохое или бессмысленное: многие задачи решаются им на порядок проще.
Немного пугает то рвение, с которым его несут в массы.
Sorry :)
.
.
так, для справки — Маргарет Корасик все-таки женщина :)
Как решить задачу "Timus 1158 — Censored!"?
С помощью Ахо-Корасика .
Добавляем все строки в бор, считаем суффиксные ссылки. Далее считаем динамику, где состояние — длина строки + состояние в Ахо-Корасик, а значение динамики — количество строк такой длины, которые хорошие и заканчиваются в данном состоянии. Хорошими считаем строки, которые ни разу не побывали в состоянии, из которого по суфф ссылкам достижимо терминальное.
ДП. Будем строить всевозможные предложения начиная с пустой строки и прибавляя букву за буквой. Для того чтобы нецензурное слово не оказалось подстрокой предложения достаточно помнить некоторые предыдущие сказанные буквы. Нас интересует наидлиннейший суффикс уже построенной части предложения, который является префиксом некоторого нецензурного слова. Перебираем все буквы алфавита, прибавляем их к суффиксу, пересчитываем наидлиннейший суффикс полученного предложения.
PS: для вычисления всех этих суффиксов-префиксов можно построить граф "в лоб" или используя Ахо-Корасик.
UPD: еще нужно удалить все нецензурные слова в которых присутствуют как подстроки другие более короткие.
Спасибо
Hello, how would you write the matching function for the structure? I tried to do it in this way: The first thing is to pass for every node on the trie and when the node is an end of word i do something with it, but i still have to go to its kmp links because it may have some other matching.
great post. thanks !!
how to write output function ?
I have been trying: TIMUS-1269 Getting Memory Limit Exceeded on test #7. What is the workaround for this?
It's been a really long time but have you solved it ?
It may be too late, but I just divided all obscene word into two parts. Then I run Axo-Corasick algorithm separately by building a trie for each part again. It has already discussed on discussion of problem.
SPOJ — Morseকেন Morse ভাই?
SPOJ — Morsekeno
Morsebhai?SPOJ — Morseকেন
Morseভাই?What does the array term[] in your code do here ? What does this array store here?
163E - e-Government
is also a aho problem
SWERC16 E — Password
:)
tnx
nice :)
another problem
*you need to have a lightoj account to see the problem.
Check this list
Is there any problem like : "Find all strings from a given set in a text (or count the number of times each string from a list appears in a text)" ? I try to find one to text my code ...
Thanks in advanced!
Kattis String Multimatching
Thanks so much!!
Try this problem
Try this problem too:Codechef Twostr
please correct me if i am wrong — we are trying to make failure links for the nodes just like LPS array of KMP..
also — how can i solve https://cses.fi/problemset/task/1731 using the same algorithm?