mirceadino's blog

Minimum path cover in directed acyclic graph (paths not necessarily disjoint)
By mirceadino, 10 years ago, In English

Hello everyone! I have difficulties in solving the following problem (it's from a Romanian judge):

Given a directed acyclic graph with N nodes (1 <  = N <  = 100) and M edges (1 <  = M <  = 5000), find the minimal number of paths necessary to cover the graph (that means that each vertex is contained in at least one path). Paths are not necessarily disjoint, so a vertex or an edge can be part of multiple paths.

For example, for N = 7 and M = 7 and the following edges:

1 2
7 2
2 3
2 4
3 5
4 5
4 6

the answer is 2 (one path may be 1->2->3->5 and the other 7->2->4->6).

Thank you in advance!

Edit: Case solved, see mmaxio's indication and xennygrimmato's link.

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Find the transitive closure and solve the problem for disjoint paths.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you also provide me a brief proof?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      It's not hard to see how to transform a cover of G into a disjoint cover of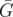 without changing its size(replacing paths with an edge), and vice versa.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Can you please explain your approach a bit more? I'm having some difficulty understanding it.

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Maybe this and this could help.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    These help solving the problem after following mmaxio's indication. Thank you too!

    → Reply