→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 11:11:57 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











why it appears " Comments (3)" ,but there is nothing in comment(of course not count this), is this a bug or comments are deleted?
Illuminati, I'm su-
Could you upload the contest to gym after it's over?
I really enjoy your contests, but the time is usually unsuitable for me :(
That's a good idea. I'll see if it is possible.
thank for informing...i joined it
Oof. Got everything, but with over 9000 bugs, most likely. I had to rewrite some codes from scratch because I didn't read some clarifications until late in the contest...
For the hardest problem, I used divide and conquer with BIT in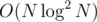 .
.
Also, (now correct) codes: MOBITEL UTRKA STUDENTSKO BOB SUMA NORMA.
How did you solve C?
Compress the numbers into a permutation of 0..N - 1. Then, divide them all by K. You're left with sorting this sequence in as few steps as possible, which has been in CF before — you just need to sort the complement of the longest non-decreasing sequence. Can be done in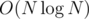 , but O(N2) is sufficient here.
, but O(N2) is sufficient here.
I did the same.
Nice, it's also possible to solve the problem using divide and conquer in O(N log N). And there is data structure + sweepline solution in O(N log N).
Can you explain norma (6th problem) in more details, please?
Sure. It's probably clear that the divide and conquer solution splits an array into 2 of equal halves, recurses into the 2 halves and adds the sum for sequences that are formed by merging parts of both halves; the key is in doing that merge.
We can list all prefixes of the right half and suffixes of the left one as triples (min, max, len). If the left part contains the minimum (equal minima also fall under this case), we can sort them by min and iterate over non-increasing min while adding right parts whose min is > = . Now, another fork comes: the max of the left half can be larger or smaller than that of the right one. In the first case, we need the sum of minlmaxr(lenl + lenr) for maxr > maxl; in the second one, the sum of minlmaxl(lenl + lenr) for maxr ≤ maxl. We just need to compute the sums of 4 values in 4 BITS for that and evaluate the sums of each of these 4 terms from them for fixed l. The case minl > minr is very similar.
Thanks!
is this approach correct? we first sort our array first we say that dp[i] = minimal*L of the subsequences which ends with i which is sumdp[i-1](sum of dp[0] till dp[i-1]) + 2^i-2*arr[0] + 2^i-3*arr[1] ... + 2^0*arr[i-1] + arr[i](for the alone arr[i]) which we save this amount in sum and we do sum=sum*2+arr[i] and then at the end we multiply dp[i] by arr[i] and add it to our final answer
Edit: it is incorrect but it can be solved like this
How much points did you got from last problem?
Full score (the results are public now on the evaluator).
48 with segment tree
You can write Sparse Table and it will be 64 points.
without sparse table and segment tree, 64 points http://ideone.com/uO6SrE
lol,I solve problem D,E but I can't solve C still,can someone help ?
How to solve D?
you need to construct for each i row array b: where b[i][j] means maximum k that a[(i-k,i)][j]=1 then you can easly find: how many rectangles ends in (i,j) point. sorry i know my english is bad (( so you can check my code http://pastebin.com/YGgehUFM
How many point you got ?! I'll bet that it's not more than 50 point!
He got 0 :)
Why do you think so? and what's your solution?
I solved it using DSU + Sweepline! (I think it must have an easier solution)...
My Code
Can you explain your solution in details?
your function "solve" can be called O(nm) times every time it is called it calls the sort function which has complexity O(n log n) so how is your solution is the fast?
lets say X is size of vector v.
every time I call solve function it is O(X.log X), and we know there will be n.m object in vector v. so my algorithm comlpexity is O(n.m.log n)
I found his name at scoreboard and saw his points for problem D. I wrote N^3 solution and got 70 points.
yes all of you are right, my solution was incorrect,but its near to correct solution,here i will explain correct solution you can see: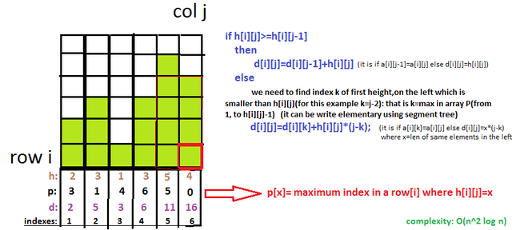
O(N(logN)2) for hardest problem deserves better then %50, isnt it?
EDIT: it seems my implementation was bad, since there is full score with same solution.
Is it possible to solve D problem with DP? I got 24 points using DP. I knew it was wrong but I tried to get some points.
This is what I tried:
t[i][j] -> Value at row i and column j.
dp[i][j] -> Amount of rectangles ending at row i and column j.
row[i][j] -> Amount of the last consecutive equal values ending at column j in row i.
col[i][j] -> Amount of the last consecutive equal values ending at row i in column j.
Then:
dp[i][j] = 1 + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + (t[i][j] = = t[i][j - 1]?row[i][j - 1]: 0) + (t[i][j] = = t[i - 1][j]?col[i - 1][j]: 0 + (t[i][j] = = t[i - 1][j]&&t[i][j] = = t[i][j - 1]&&t[i][j] = = t[i - 1][j - 1]?X: 0))
I can't get the value X in this dp.
Is this a correct approach to this problem or am I completely wrong? If somebody solved this problem using DP I will thank if he/she explains the approach. Thanks in advance.
I think there is no O(NM) DP solution. Problems of this type have a standard solution using stack that can be slightly modified to compute what you need.
Thanks!
Could you please, if you have some time, explain the main idea behind the Standard solution for this kind of problems. Thanks in advance!
Here, a simpler version (finding the maximum size, not number of rectangles, which is just a matter of using a different formula) is described, try to work based on it.
Thanks! I will check the 4th approach: Linear search using a stack of incomplete subproblems