Задан массив A и задаются запросы l r x. Ответ это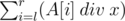 
где div операция целочисленного деления. Хочется увидеть решение онлайн. Не могли бы вы подсказать как решается эта задача? UPD: Всем спасибо за ответ!
→ Обратите внимание
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | Benq | 3676 |
| 2 | jiangly | 3670 |
| 3 | Kevin114514 | 3657 |
| 4 | maroonrk | 3355 |
| 5 | Um_nik | 3353 |
| 6 | squareOf105 | 3346 |
| 7 | tourist | 3343 |
| 8 | strapple | 3324 |
| 9 | heuristica | 3322 |
| 10 | jiangbowen | 3291 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | Qingyu | 158 |
| 2 | nik_exists | 150 |
| 2 | maspy | 150 |
| 4 | AmShZ | 143 |
| 5 | Um_nik | 141 |
| 6 | Errichto | 139 |
| 7 | adamant | 137 |
| 8 | BledDest | 134 |
| 9 | maroonrk | 133 |
| 10 | qwexd | 130 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2026 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 14.10.2026 15:25:19 (g2).
Десктопная версия, переключиться на мобильную.
При поддержке
Умею за C*n предподсчета и ответ за log^2(n) * MAX_A / C (Видимо C должно быть ~ sqrt(log^2(n) * MAX_A)) Если q ~ n
Для всех X <= c префсуммы.
ДО. В каждом вершине все элементы. Далее запрашиваем префсуммами честную сумму, далее спрашиваем "склько чисел больше либо равны x?", "сколько больше либо равны 2х", на такой запрос легко отвечать за log^2(n).
Можно ли эффективно решить если MAX_A < 10 ^ 18?
Я не умею:)
Вряд ли.
Какие ограничения на
времени и 
памяти отвечать на запрос за 
: для x ≤ k предпосчитать суммы на префиксах, для x > k ответить на 
запросов вида "сколько чисел ≤ t на отрезке" (решается за O(nlogn) времени и памяти для предпосчёта и O(logn) времени на запрос). Выбор k зависит от того, насколько жалко памяти и каково отношение числа запросов к n.
A[i]? Если длина массива равна n, A[i] ≤ MAXA, то можно с предпосчётом заUPD. Надо обновлять страницу перед посылкой.