Hi. In this entry I want to discuss the score distribution and drain of points (by that term I mean how fast points value of problem is becoming smaller) in longer contests (joint ones like #270 or ZeptoLab). In my opinion everything (drain + typical distribution) works fine in regular contests, but not in those longer ones.
Due to standard habits adjusted to regular contests, distribution in longer ones (typically 7 tasks with difficulty similar to Div2A, Div2B, Div1A, ..., Div1E and 2,5/3h) is similar to 500-1000-1500-2000-2500-3000-3500. Also, contests are longer, so task submitted in the end of 3h contest is worth only 30% of its original value (drain is 0,4% of original value with every minute, but resulting in not lower value than 30% of original one, even when wrong submissions are taken into account). Then, having accepted problem worth 3500 pts after 2h and 55 mins without any previous wrong submissions is worth 1050 pts, while D submitted after 0,5h is worth 1320pts — much more than 1050 pts (even after 1h it will still be 1140pts) — it is clearly unreasonable! Then, if someone made a small bug in D or received random TLE, he will likely end up in a very bad position even though he did the hardest problem!
In my opinion, joint contests need special treatment for them to be fair. In my opinion ideal score distribution should be like 250-500-750-1000-1500-2000-2500 and drain should be smaller, scaled in such a way that if someone submits something in the end of contest it is worth 52% of original value (like in regular contests). There is a sufficient number of joint contests to make this issue important (for example — CF #270, MemSQL Round 1, MemSQL Round 2, upcoming Bayan Warmup, ZeptoLab, Rockethon). I hope that proposed solutions are not a problem from technical point of view (at least changing typical distribution should be no problem, adjusting drain may be more complicated).
What do you think about this? Share your opinion.











From the other side, giving a shot on the hardest problem at the beginning of the contest is a risk which should be awarded.
I think that you are not familiar with this algorithmical problem:
You are given n tasks. i-th task takes you ti minutes and you have to pay ci for each minute of delay (if you complete this task after k minutes you pay k·ci). You can do one task at time. What is the order of completing task, which minimizes cost?
This is an easy problem and it is exactly case of optimal order of doing task on contests. Correct answer is to sort tasks increasingly by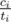 . It is a rare case that on CF it is other than ABCDE :P.
. It is a rare case that on CF it is other than ABCDE :P.
But leave that thing alone. Drain of points here is irrelevant, whatever order we will choose it is just a scaling of penalty. Score distribution I proposed is more rewarding doing hard problems than those easy ones (which is reasonable that hard problems should be awarded more than easy ones even when solved lately), their value ratio is enlarged to regular value, so your argument is not "from the other side" it is confirming my point :). So thank you for your support :D.
We can see CAB or ECAB strategy being helpful for non-zero number of contestants in every round, because it happens that problem E does not consume more time thinking/coding than C for some people in a particular round.
It does not really confirm your point, because if we slow down draining of points for E, it won't give risk-taker a big advantage above those who are doing ABCDE.
Can you provide an example? I claim that with very safe assumptions like "E is never easier than C" such example doesn't exist, especially when standard Div1B and D values are enlarged from 1000 and 2000 to 2000 and 3000.
Look at riadwaw's last round action.
That is definitely not the answer I was hoping for. Maybe it was a miscommunication. I didn't want to know an example for why it is sometimes better to try problems not in an alphabetical order but, why do you think that slowing drain won't give such a big advantage.
I think so because one does not have to skip ABC(to risk) when he wants high points for DE.
I requested for example with sample detailed scenario of events (guy A does that problem in that moment, another in that moment etc, guy B does that problem in that moment etc. and considering faster and lower drain we see that the situation with faster drain is more fair, because guy A would have that amount of points and guy B that amount, but it is unfair, because something).
For me now, these are merely words without any confirmation in reality.
Stop arguing, be like real programmers and
fight till deathprove your point here. You can adjust problem costs as well as some CF parameters to see how people will jump around the table.P.S. : sometimes list of contests on top doesn't load, feel free to hit F5 then.
告訴我怎麼解決問題?...
$2a$08$0ZNOXOxqHbdZQGps3KHjBuyk0WqDndHiv8s6WqRkktUhNFqZBHdM!
+hos.lyric
Yes. Good idea. Of course, the problem cost depends on the author, too, but harder problems should be rewarded (at least roughly) proportionally more than easier ones.
This distribution makes CF scoring something between ACM and TC ones (proportional is between constant and exponential :D), but this way, it can get skewed towards ACM too much — considering the expected order of problems by difficulty is known.
Hmm, it'd be fun to organise contests with various rule mixtures. For example, equal point distributions and random order of problems, but with CF rules otherwise. Of course, I mean fun for the organiser :D
I think your point is not only true for joint contests but for regular contests as well. For example (if we forget about the drain for a second) in regular div. 1 contest problems A and B together have the same cost as C (1500 points). At the same time if you look at the second division then solving the same problems (C and D) there is much better than solving just one E — you get 3500 points instead of 2500! And this seems to work the same way in the joint contests, we add two more easy problems and they change the effective relative score of the harder problems.
Though in order to make it right all you need is to make scoring kind of geometry progression, instead of arithmetic.
Usually the first three problems of d1 are 500-1000-1500. The same problems are used in d2 as 1500-2000-2500. I think geometric progressions are more natural, for example, 480-720-1080-1620-2430.
Best proof that this drain definitely needs to be changed -_-.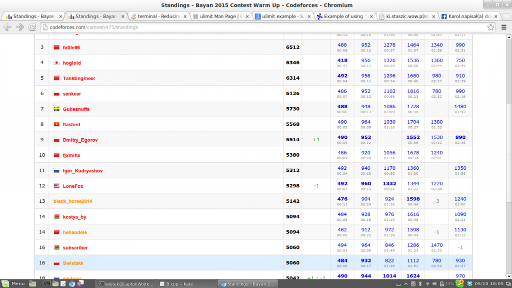
FYI, These are standings before systests from Bayan WarmUp. 7 people got pretests passed on all problems. 6 of them are on positions 1-6 and I'm on 16th place ; d... That is because I chose to do them in more or less alphabetical order. I got 5 wrong submissions, but for 6 problems it's not that many, I think.
I hope that at least >=5 problems will get AC. However it is sad that my submissions for E and F are worth less than B...
UPD: Just FYI. C and F failed. C because of some bug, F because it turned out that I think I got right idea, but used that in a very stupid way and my code is in fact equivalent to bruteforce :/.
i was thinking of posting about this score problem but then i saw your post :)
the same thing happened to me in Bayan WarmUp 7 i solved E at the end of contest but only got 770 points for a 2500 problem
i agree that the score distribution has to change.
That is because I chose to do them in more or less alphabetical order.
But you said it's the only optimal strategy.
F turned out to be harder than I expected, so I withdraw my statement that I should have done F before C and E demanded loads of code, it was consisted of two main parts (firstly divide graph into two-connected components and transform it into weighted tree and secondly solve some funny problem on tree), but I was lucky enough to have both of them already coded, so I just copy-pasted my two old codes and adjusted second one to version with weighted tree, not unit one, so this was really an exception in my case.
Don't ever let yourself to ignore skype messages.
I'm so lucky that I did remember to close RedTube before capturing that picture!
Could have been worse, at least B (which was worth more) didn't fail!
Exactly what I have thought when I saw that B got AC — "Now everything else can fail, B was worth more than almost all other problems" :P.