Новая структура данных для решения задач, связанных с подпалиндромами в строках:
http://adilet.org/blog/25-09-14/
Спасибо пользователю droptable, который поделился этой информацией!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Новая структура данных для решения задач, связанных с подпалиндромами в строках:
http://adilet.org/blog/25-09-14/
Спасибо пользователю droptable, который поделился этой информацией!
| Название |
|---|



Сборы в Ижевске же вот-вот начнутся, а ты уже в открытый доступ выкладываешь...
Хм, лекция по структуре данных, данная в Петрозаводске, это не то же самое, что архив сборов, так? К тому же не факт, что такая же информация будет доступна в Ижевске.
Эта информация используется в задачах. А ты её спойлеришь раньше времени. Архив сборов, кстати, как я понимаю, доступен только их участникам.
Я нигде не говорил, что эта информация используется в задачах.
И в целом, независимо от того, где это используется, я считаю что дерево палиндромов — общий алгоритм для широкого класса задач, и такая полезная информация должна быть в открытом доступе. Если бы я написал, скажем, про поиск в глубину или суффиксный массив, про которые кто-то рассказал мне в Петрозаводске, это тоже было бы "спойлером"?
Плюс, насколько я знаю, информации в интернете по этой теме пока еще нет (разве что где-то в paper'ах), случайно на контесте это врядли кто-то придумает, так в чем смысл прятать алгоритм? Чтобы его случайно кто-то где-то не использовал?
Я совершенно не думал ни про какие сборы, когда писал статью, и извиняюсь, если вдруг его кто-то где-то применит и он на что-то повлияет.
Кто-то еще умудряются тебя минусовать. Так и хочется от души надавать им по рукам.
Разве не разумнее было бы написать подобное замечание в ЛС автору — чтобы он отредактировал тему или спрятал ее в черновики? Вместо того, чтобы становиться соучастником:)
В целом ведь хорошая тема, если бы не упоминание о ПЗ/Ижевске. Тогда получилось бы так — кто прочел и разобрался, тот молодец; кто не прочел — сам виноват.
Безусловно, было бы. Но я слишком дурак, чтобы сразу принимать адекватные решения.
Дурак, который понял, что он дурак, им быть перестал.
На Codeforces дураков — тысячи, если не десятки тысяч. Риторический вопрос: какой процент из них способны на такой подвиг?
У меня сейчас возникла такая картина — открываю я эту тему через пару дней, а у этого комментария -1000 :D
А я не удивлюсь такой картине, только мне от нее скорее захочется плакать.
Я сейчас очень сильно ностальгирую Codeforces двух-трехлетней давности, в частности, по постам Саши Куприна и по резким высказываниям Паши Хаустова.
Сейчас они отсюда ушли, а понаприходили всякие "Hi! I am new, please help!" серо-сине-зеленые, г-н Рубинчик со своими пиар-штучками, Bredor и т.п.
И это печально. :(
Блин, ну чего ты, Bredor — это цветное, не ругай его!
Вот через пару лет какой-нибудь Александр будет ругать новое поколение серо-зелёных и ностальгировать по бредору...
Через пару лет, возможно, даже я буду ностальгировать по Bredor'у.
It looks like manachers palindrome algorithm. It also works in O(N). I mean it uses the same logic. I dont say that they are completely the same.
What about implementation ?
It's here
.
Предположим, что на сборы в Ижевске поедут какие-нибудь не самые сильные команды из УрФУ, участники которых не участвовали в подготовке УрФУ-контеста — соответственно, они будут писать этот контест. Однако, они вполне могли слышать про Ваше дерево палиндромов. А теперь предположим, что ADJA не создал никакого поста.
И в первом случае одни участники не знали о структуре, а другие знали, и во втором случае одни участники не знали о структуре, а другие знали. Но есть один нюанс...
.
По поводу сборов в Ижевске тут другой вариант — автор знал о существовании сборов, не знал дат (хотя их, конечно же, можно было узнать), но совершенно забыл об этих сборах на протяжении последних пары недель точно.
Единственная проблема сейчас, насколько я думаю, лишь в том, что сборы в Птз и Ижевске теперь возможно нельзя будет со 100% точностью сравнивать. В целом, остальные доступные алгоритмы тоже читали не абсолютно все команды, и ссылок принудительно не давали. Тут разница наверное в том, что на возможную связь дерева палиндромов и сборов заострили внимание в комментариях.
Название структуры на palindromic tree обязательно изменю, как доберусь до нормального компьютера.
Еще раз сорри, если нарушил какие-то планы или негативно на что-то повлиял.
This algorithms complexity is guaranteed O(n) or generally O(n). I learn algorithm but I don't understand algorithms complexity. My opinion this algorithms complexity maybe O(n*log(n)).
I think , it is guaranteed O(n) , cause left side of 't' is always pointing to a index less than or equal to the index being added (x) & its always increasing , so it will need at most n iteration .
I got it. Thank you!
For part of article that says: 'a string of length n can have at most n palindromic substrings'. Is the following how you prove it?
Pf. Worst case is characters are all different, in which case there are exactly n palindromes each of size 1. Other case is when there are at least two similar characters: suppose that string looks like
**ya****ax***wherex != y. Suppose thata****ais a palindrome, so there arelength(a****a)/2palindromes in that substring. So if remaining letters are all distinct, string has:length(a****a)/2 + n - length(a****a)/2 = npalindromes.well, I didn't try to understand your proof. One easy way to prove it:
See on the all of palindromes that ends on position i, all except largest of them appeared before (because they are also prefixes of the largest one). So adding 1 letter adds at most one new palindrome.
Problems recommanded:
HDOJ 3948: The Number of Palindromes
CERC14 G: Virus synthesis
Xi'an14 G: The Problem to Slow Down You
A part of the article says: "The string xAx is the only palindrome substring of p + x, that we possibly never saw in p. To understand why this is so, notice that all new palindrome substrings which we didn't meet in p must end on that last letter x, and therefore be the suffix-palindromes of p + x. Because xAx is the largest suffix-palindrome of p + x, all other smaller suffix-palindromes of it can be found in some prefix of xAx (since for any suffix of the palindrome there is a corresponding similar prefix), and therefore we alreay saw them in p". What is the meaning of this part ?
This part tries to tell U every time we add a letter, the number of new palindrome may increase by one or not.
It's easy to understand since xAx is the largest suffix palindrome and if there was a new palindrome it must be ended with the letter we added now. And since xAx is the largest suffix palindrome, this new palindrome's left bound will be in the range of xAx. But if a substring Bx is a palindrome, and the left bound of B is less than xAx, we know xB'(B' is the reverse of B) is also a palindrome, and it appears in the left part of xAx, and not ended with right x. So it has appeared. So xAx is the only substring which may be a new palindrome.
Thanks. I got it
I just got a nice question regarding palindromic tree in my blog
Question (if I got it right): can we produce the same arrays as Manacher's algorithm does — i.e, largest odd/even palindrome with a middle in this position — using palindromic tree?
I didn't come up with an answer right away, so do you know how to do this? You can write it here or in the blog.
We can. But I don't know any way to calculate it easier or faster than in Manacher's algo. The most obvious way is bin search + check if [l..r] is a palindrome.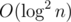 .
.
Hi, thanks for an answer. How would you check that substring in [l..r] is palindrome using palindromic tree?
Palindromic tree problems: 1) http://www.spoj.com/problems/NUMOFPAL 2) http://www.spoj.com/problems/LPS