Codeforces Round #268 Editorial

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

I'll upload my example solutions and will post links to them as soon as it becomes possible.

All the problems in Div 1 don't have the unique solution. I list several solutions to each problems. There are also some interesting bonus problems. I can't solve some of them yet :( If you have interesting ideas, feel free to share and discuss your ideas in the comments. :)

My English is poor, so if there are some mistakes or something you can't understand, you can also discuss it in the comments.

469A - I Wanna Be the Guy

I Wanna Be the Guy is an interesting game. I strongly recommend it to you.

The problem itself is easy. Just check if all the levels could be passed by Little X or Little Y.

7894174

469B - Chat Online

This problem is not hard. Just iterator over all possible t, and check if the schedule of Little X and Little Z will overlap.

7894252

Bonus:

p, q ≤ 50, l, r ≤ 10⁹
p, q, l, r ≤ 10⁵

468A - 24 Game

Solution 1:

If n ≤ 3, it's easy to find that it's impossible to make 24, because the maximal number they can form is 9.

If n > 5, we can simply add n - (n - 1) = 1, 24 * 1 = 24 at the end of the solution to the number n - 2.

So we can find the solution of 4, 5 by hand. 1 * 2 * 3 * 4 = 24, (5 - 3) * 4 * (2 + 1) = 24

7894267

Solution 2:

We can find the pattern like that n + (n + 3) - (n + 1) - (n + 2) = 0, and find the solution of 4, 5, 6, 7 by hand or brute forces.

Solution 3:

A knapsack-like solution.

7894283

468B - Two Sets

Solution 1:

If we have number x and a - x, they should be in the same set. If 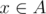$\text{[math]}$ , it's obvious that 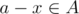$\text{[math]}$ . The contraposition of it is 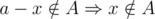$\text{[math]}$ , that means if 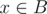$\text{[math]}$ , a - x should in the set B. Same as the number x, b - x.

So we can use Disjoint Set Union to merge the number that should be in the same set.

If a - x doesn't exist, x can not be in the set A. If b - x doesn't exist, b can not be in the set B.

Then check if there are any conflicts among numbers which should be in the same set.

There are many other solutions to solve this problem based on the fact that x, a - x, b - x should be in the same set, like greedy, BFS and 2-SAT.

7894313

Solution 2:

If a = b, it's easy to find the solution.

We regards every number as a node. Every number x links to number a - x and number b - x.

The degree of every node is at most 2. So this graph consists of a lot of chains and cycles, and some node may have self loop.

We only need to check if the lengths of all the chains are even or the chain ends with a self loop.

7894323

Bonus:

Prove there is no cycle in the graph described in the solution 2.

Divided all the numbers from [0, n - 1] into two sets that have parameters a, b. Can you solved it in O(1)?

468C - Hack it!

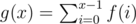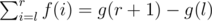Define $\text{[math]}$ . $\text{[math]}$ , so we should find a pair of number a, b that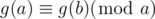 $\text{[math]}$

Solution 1:

First we choose x randomly. Then we can use binary search to find the minimal d that 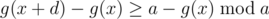$\text{[math]}$ .

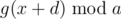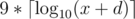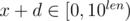So $\text{[math]}$ is very small, between 0 and $\text{[math]}$ . If $\text{[math]}$ , after choosing x atmost 9 * len + 2 times, we can definitely find a pair that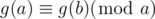 $\text{[math]}$

7894341

Solution 2:

We can use binary search to find the minimal d that g(d) ≥ a, g(d) ≥ 2a, ...

This solution is similar to the first one.

7894452

Solution 3:

We can use binary search to find the minimal d that g(d) ≥ a. And we use two pointers to maintain an interval [l, r] that 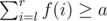$\text{[math]}$ until we find $\text{[math]}$ .

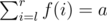I can't prove the correctness of this algorithm, but it performs well in practice.

7894356

Solution 4:

Thanks ZhouYuChen for his talented idea.

If x < 10¹⁸, we can get f(10¹⁸ + x) = f(x) + 1. That means if we shift the interval [x + 1, x + 10¹⁸] by 1, the result will be increase by 1 too. And it also not hard to find that g(10^x) = 45 * x * 10^x - 1. So if 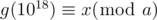$\text{[math]}$ , [a - x, a - x + 10¹⁸ - 1] is the answer.

It's easy to see that upper bound of the answer is a, because of pigeonhole principle (among g(0), g(1), ..., g(a) at least two are equal). So big integer is not required in this problem.

If solution 3 is correct, the upper bound of the answer can be 2 * 10¹⁶.

7878473

Bonus:

Prove or disprove that solution 3 is correct.

468D - Tree

I am sorry that this problem coincides with that one.

d(u, v) = dep_u + dep_v - 2 * dep_LCA(u, v), so the answer is:

$\text{[math]}$

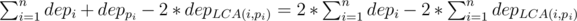
dep_i there means the distance between node i and root.

We choose centroid of tree as root (let's denote it u), so we can make every pair (i, p_i) are in different subtrees, that means dep_{LCA(i, p_i)} = 0.

So the answer is 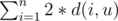$\text{[math]}$ .

The next part of this problem is find the lexicographically smallest solution.

We regards it as finding the lexicographically smallest matching in a bipartite graph.

For a subtree, if the amount of nodes in this subtree in the left part > the amount of nodes not in this subtree in the right part, the perfect matching doesn't exist. So the amount of nodes in this subtree in the left part + the amount of nodes in this subtree in the right part should be no more than the amount of nodes unmatched, while the root is an exception.

We can use a segment tree to maintain it easily. We determined the minimum possible p_i from 1 to n. If there is a subtree that the amount of nodes in this subtree in the left and right part is equal to the amount of nodes unmatched, we must select a node from it, so p_i equal to the node in this subtree with the minimum id. Otherwise, we can choose a node with the minimum id that is not in the same subtree with i.

7894417

468E - Permanent

The permanent can be obtained as follows: for each (e₁, e₂, ..., e_t) such that x₁, x_e₂..., x_{e_t} are distinct and y_e₁, y_e₂, ..., y_{e_t} are distinct, add 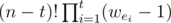$\text{[math]}$ to the answer.

It can be proved by the formula :

$\text{[math]}$ ,

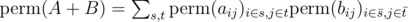where s and t are subsets of the same size of {1, 2, ..., n} and 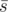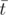$\text{[math]}$ , $\text{[math]}$ are their respective complements in that set.

Construct a undirected graph G with 2n vertices v₁, v₂, ..., v_2n, where the edge weight between vertex v_i, v_n + j is A_i, j - 1. We only need to know the sum of weight of all matchings that we choose t edges. The weight of matching is the product of all edge weights in the matching.

We only need to know the sum of the weights that we choose x edges in the each connected components.

The number of nodes in a connected component is s and the number of edges in this connected component is t.

Algorithm 1:

Because it's a bipartite graph, so the number of vertices in one part is at most s / 2. So we can use state compressed dp to calculate the ways to choose x edges in this connected component. The complexity is O(2^s / 2 * s²).

Algorithm 2:

We can choose a spanning tree. The number of edges in spanning tree of these vertices is s - 1, and the number of non-tree edges is t - s + 1. So we can enumerate all the non-tree edge, use tree dp to calculate the ways. The complexity is O(2^t - s * s²).

Combined with these two algorithm, the complexity is O(min(2^s / 2, 2^k - s) * s²)) = O(2^k / 3 * k²).

Комментарии (60)

Показать архивные | Написать комментарий?

RedLord

10 лет назад, # |

468A — 24 Game Solution 3: A knapsack-like solution.

Can someone explain it?

→ Ответить

aranjuda

10 лет назад, # ^ |

← Rev. 2 →

From the link posted in the editorial, this is what I got:

The crux of the solution lies in the equation: Pos = (Tn + 24)/2. Pos is the sum of the first k numbers with some number x removed. Tn is the sum of the first N numbers (N is input).

This means 2*Pos - Tn = 24 We can reduce this:

2*sum(1..k) &mdash; sum(1..n) &mdash; 2*x = 24

sum(1..k) &mdash; sum(k+1..n) &mdash; 2*x = 24

sum(1..x-1) + sum(x+1..k) &mdash; sum(k+1..n) &mdash; x = 24

For example, for test 2, x = 6 and sum(k+1..n) is 0 [k has to be <= n]

For test 3, x = 4 and k+1 = 11 For N = 7, x = 6 (this case was tested twice — so was N = 3, am not sure why?)

andreyv

Does 468B - Two Sets contain anti-hashtable tests? I'm curious why my submission TLed with unordered_map/unordered_set and passed with regular map/set.

jqdai0815

No. test cases are randomly generated.

LeoSko

+20

map/set has O(log(N)) complexity of []operator/find().

unordered_map/unordered_set: O(1) on average, but in worst case O(N).

Rubanenko

Thank you so much.

shank_punk

+30

Div2 C problem is really good. Hope that the next codeforces round is as good as this one. Thanks for exposing us a lot of good problems.

Thank you :)

← Rev. 6 →

"If n ≤ 3, it's easy to find that it's impossible to make 24, because the maximal number they can form is 6."

A minor error there, the maximal number they can form is 9. 3 * (2+1) = 9

Also, could you please elaborate on the idea for the knapsack-like solution?

sorry, you are right :P

I_love_Tanya_Romanova

What is worst possible case for div1C-solution 3? I mean test with largest possible L.

HekpoMaH

Then check if all the number should be in the same set can be in the same set.

Can you rephrase it? I find it difficult to understand what you mean. Possibly there is a comma (,) missing?

After doing the stuff described above it turns that some pairs of elements should be in the same set. So you have to check whether it is possible to divide them between exactly two sets satisfying the condition.

← Rev. 5 →

Can someone elaborate all the solutions for problem B Two Sets? (Solution A, B, Greedy, 2 SAT and Hopcroft-Karp)?

I can't understand what's given in the editorial.

Here's what I've collected so far:

Solution 1: How do you do this "Then check if there are any conflicts among numbers which should be in the same set." (which is the essence of the problem I guess) Code from editorial

Solution 2: "So this graph consists of a lots of chains and cycles, and some node may have self loop." Why does there exist no cycle? Chains exist in the following way: x -> a-x -> b-(a-x) -> a-(b-(a-x)) -> ... (prove this sequence is finite)

Self loops exist when x = a-x or b-x, i.e. 2x = a (or b)

"We only need to check if the lengths of all the chains are even or the chain ends with a self loop." Why is this true?

Code from editorial

O(1) solution: Awaited.

Greedy: Code & Explanation

Hopcroft Karp: Code (Explanation added would be helpful)

2 SAT: Not found anything yet.

I mean editorials are for the people who couldn't solve the problems, right? Some more details in explanations would be useful I feel.

Thank you for your questions.

Ques 1: First you know number x, a-x, b-x should be in the same set, you can use DSU to maintain it. For one set in the DSU, the numbers in this set should be in the same set. If one number x can't be in the set A, it can only be in the set B. If one number y can't be in the set B, it can only be in the set A. So if number x and y should be in the same set, there is no solution.

Ques 2: If the lengths of a chain is odd, two ends must be in the different sets. For example, a=7, b=9, 3-4-5.

Ques 3: Divided all the numbers from [0,n-1] into two sets that have parameters a, b. I don't want to explain it, because this one is definitely a math problem. Don't relate much to the algorithm contest. I hope you can understand. If you want to know the answer to this problem, I think writing a brute force problem and finding the regular pattern is a good way.

Ques 4: I think Hopcroft Karp algorithm and 2-SAT algorithm do the same thing as solution 2. Because this graph is so special.

Thanks :)

DieAnderen

according to wiki, "the Hopcroft–Karp algorithm is an algorithm that takes as input a bipartite graph", but the graph described here isn't always bipartite.

I used 2SAT to solve this problem, here is the code: 7883574

p-space

may someone provide a better explanation for the C-div1 first solution ?

lizhi890611

← Rev. 4 →

The basic idea is to shirk the search space and using the pigeonhole principle.

First, we chose a random number x, and find the minimum d such that G(x + d) >= a (also know G(x + d -1) < a since G(x) is a monotonic function). Since G(x + d) = G(x + d- 1) + f(x + d) and the biggest possible value of f(x + d) is 9 * ceil(log10(x + d)), G(x + d) % a should be less than 9 * ceil(log10(x + d)). If for all x + d belong to [0, 10^len), then G(x + d) % a must also belong to [0, 9 * len] for different x.

Now, We just fill numbers into this search space for different x, and we must can hit the same value because of pigeonhole principle (at most 9 * len + 2 times).

shadow_crawler

How can i calculate g(x). I mean the summation digits of numbers from 1 to x...?

thanhdno

14 месяцев назад, # ^ |

NuM

"In the solution 4 we can find that the upper bound of the answer is 2 * 10¹⁸. So big integer is not required in this problem." (problem C)

Easy to see that upper bound of the answer is a, because of pigeonhole principle (among g(0), g(1), ... g(a) at least two are equal).

OwO you are right.

Swistakk

Was that really necessary to set a up to 10¹⁸ :(? I came up with the second solution (though, after the contest, because I hate sums of digits problem, but that one turned out to be pretty fun :P), but I was unable to code it properly (I code in C++), because I had to deal with numbers of magnitude approximately 1000*a, I think. And moreover afaik Codeforces is not supporting __int128_t...

I_love_Hoang_Yen

I think that it is necessary to set a as high as possible.

If a is around 10^10, the following could pass: Generate 10^5 random integers. There should be a pair (l, r) such that f(l) = f(r) mod a

If a is around 10^16, I could modify the above a bit to make it work:

Instead of finding f(l) = f(r), find the pair (l, r) such that f(l) is closest to f(r) in mod a. Then use the 2 pointers method as in solution 3.

T0RRES

Somebody know how to solve problem B div.1 if we have p_i = p_j, i < > j ?

GILGAMESH

All p_i are distinct.

I know, but during the contest i don't read part where it was indicated. And now i am interested how to solve this interpretation of the problem.

http://codeforces.me/blog/entry/13836#comment-188500 This works

+21

"If n > 5, we can simply add n - (n - 1) = 1, 24 * 1 = 1 at the end of the solution to the number n - 2."
I think you should give I_love_tigersugar his deserved AC :P http://codeforces.me/blog/entry/13836#comment-188413

UPD: To explain that post — now it is fixed, but earlier there was a typo in editorial, exactly the same which caused I_love_tigersugar to fail that problem.

sea

in problem two sets- when i am first checking for x-a then there is error on test 9 http://codeforces.me/contest/468/submission/7899063 and when i am first checking for x-b then there is error on test 8.. http://codeforces.me/contest/468/submission/7899193 can any one help me??

if (a > b) {

swap(a, b);

}

ray040123

-8

There is a typo: 24 * 1 = 1

Should be: 24 * 1 = 24.

HandIeNeeded

← Rev. 3 →

In the post, this part for Problem C, Solution 4: "And it also not hard to find that ... is the answer."

Should be:

g(10ⁿ) = n * 45 * 10^n - 1 so if g(10¹⁸) = x(moda), [a - x, a - x + 10¹⁸ - 1] is the answer. (if I didn't misunderstood your g(x) function.:D)

fixed now.

krem.bananowy

I have two questions to 268 C (div 1), solution 1, because it's really unclear to me:

At some point, a variable len appears. As it is not described earlier in the editorial, what is it exactly?
What are we choosing $\text{[math]}$ times? Is it x?

thank you, fixed now.

Ioser

About problem D, I want to know, why should we choose centroid to minimize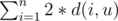 ? And what is the definition of "centroid" here? The tree is weighted. upd:maximize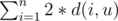

I mean, if we choose centroid as u, why is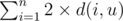 $\text{[math]}$ maximized? And, if we choose u that maximizes 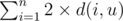$\text{[math]}$ , maybe we cannot make every pair i, p_i in different subtrees.

Sorry for my poor English.

jason_yu

I think that g(x) should be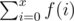 $\text{[math]}$ instead of 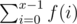$\text{[math]}$ in div1.C, or it will not satisfy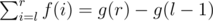 $\text{[math]}$

Thank you, fixed now.

Crucian

What is the complexity of solving the problem Div 1 D?

Could somebody please tell me what 'the left part' and 'the right part' respectively mean in Div1.D? I feel it hard to understand. Thanks in advance.

bluemmb

In problem Div2 D ( Two Sets ) , I can't understand how it is possible that splitting Odd number of elements in sets ?! because all of the elements in every set must be pair.

Can somebody help me to understand ? ( Small sample )

Sorry for my poor English.Thanks

a=2, A={1}

HidenoriS

I spent several hours to figure out the solution for Div 1 B/Div 2 D, so I wrote a solution with bunch of explanation. Hopefully someone will find it helpful.

7940575

darsh

Thank you for the explanation!

Los_Angelos_Laycurse

I think test case of Div I E is a little weak. in my code, when I choose random edge from list[], and delete the edge, it get TLE in test case 34, but if I choose edge list[0],and delete it get AC 280ms, if I choose edge list[cnt_list-1],and delete it get AC 311ms...test case should be stronger.

rr_

Can someone explain me why in Div 1 B/Div 2 D we can't just go through the numbers and for given x that is not already in the set check if there is a-x or b-x not assigned yet and put them in the correct set or if that a-x or b-x doesn't exist print "NO"? Can you give me a small example where this method falls?

More precisely — why this code doesn't work? :) http://codeforces.me/contest/469/submission/7915436

Edit: It fails on this test: 2 6 10 3 7

Edit2: Now it works on the previous test, but still getting WA. Updated code: http://codeforces.me/contest/469/submission/8051352

Project_Dimlight

The number of contestants who passed Div1.D & Div1.E is maybe too poor... I think these two problems are too difficult for a CF round. Can anyone explain the tutorial more clearly? Thanks a lot.

Problem: Hack it. (Solution 4)

Can someone explain this please...? "That means if we shift the interval [x + 1, x + 10^18] by 1, the result will be increase by 1 too."

anajin

Can we solve div1.B using exgcd ?

CMaster

9 лет назад, # |

Can someone help me to understand solution of 468B - Два множества using 2-sat?

9 лет назад, # ^ |

Nobody can't?

towrist

3 года назад, # |

In 1C: Hack It, I think setting $$$n \leq 10^{16}$$$ would have sufficed. In this version, I had to use C++ 64 bit to use __int_128 to get AC. (I came up with something similar to solution 2, with $$$x=0$$$)

Olympia

For the problem "Two Sets", how can you use 2-SAT?

Implementation w/o 2-SAT: 148934122

BerkeKaragoz

3 месяца назад, # |

-10

i failed to understand that first numbers of x and y was just counts

Thinking:

X: [1, 2]

Y: [2, 3]

X U Y: [1, 2, 3] => which covers n

Need to get more familiar with the style of the question descriptions

Блог пользователя jqdai0815