В этой задаче нужно было просто посчитать количество пар, у которых qi - pi ≤ 2
Асимптотика: O(N)
В этой задаче нужно было уметь считать количество различных битов в двух числах. Как вариант, можно просто побежать по битам и посчитать количество различных. Ещё, как вариант, если исходные два числа X и Y, то количество различных битов равнялось бы количеству единиц в числе X xor Y, где xor — операция исключающего или.
Асимптотика O(M·N)
Решение этой задачи — динамическое программирование. Изначально нужно посчитать psumR, где psumR — сумма на префиксе массива p длиной R.
Обозначим dpi, j — максимальная прибыль которую может получить Юра, если мы уже выбрали i последовательностей и последний элемент в i-ой последовательности имеет индекс j.
Очевидно, что если i·m > j, то dpi, j = 0. Иначе dpi, j = max(dpi, j - 1, dpi - 1, j - m + psumj - psumj - m) Ответом будет dpk, n.
Ещё нужно было не забыть использовать long long при вычислениях.
Асимптотика: O(N·K)
Первое, что нужно сделать, чтобы облегчить себе работу — перевести все строки в нижний регистр. Затем словам дать номера. Различным словам дать различные номера, а одинаковым — одинаковые.
Затем, из всех строк нужно построить граф. Пусть каждое слово — просто вершина. А пара слов синонимов X и Y — ребро между вершинами, которые отвечают за данные слова. Ребра ориентированные. Также, для каждого слова мы должны хранить его длину и количество букв «R». Будем использовать номера, данные словам, для построения графа.
После создания графа, у нас мог быть петли, кратные ребра, циклы. Поэтому нужно сжать все сильно связные компоненты в одну вершину. После чего задача состоит в том, чтобы посчитать dpver — пара, отвечающая за минимальное количество букв «R» и минимальную длину слова с минимальным количеством букв «R», которым можно заменить слово, за которое отвечает вершина ver.
Пересчет очевиден — dpver = max(dpnextVev, dpver), где nextVer — все вершины, в которые можно пойти из ver. Максимум из двух пар берется как у pair в C++.
Затем нужно пройти по всем словам текста, получить номер вершины, который соответствует нужному слову. Пусть это ver. Тогда к ответу нужно прибавить dpver.
Также, важно было не забыть использовать long long при вычислениях.
Асимптотика:  , где w — множество всех слов, которые есть в тексте и в словаре.
, где w — множество всех слов, которые есть в тексте и в словаре.
Данная задача решалась жадно.
Алгоритм решения такой:
Набираем числа из массива a по очереди, пока в последовательности набранных чисел(далее G) не найдется нужная нам четверка. Напоминаю, что нужная четверка чисел имеет вид: [c1, c2, c3, c4] = [x, y, x, y]. Если набрали такую четверку чисел, то добавляем в ответ. Очищаем G и v (далее будет описано, что такое v).
Очевидно, что этот алгоритм оптимален.
Для удобности сжимаем числа в массиве a. То есть каждому числу присваиваем его порядковый номер в отсортированном списке всех уникальных чисел из массива a. Это делается, потому что в дальнейшем нам удобнее использовать числа порядка O(N). Теперь как быстро узнать, что в G найдется нужная нам четверка.
Давайте для каждого уникального числа X хранить список его позиций в G. Назовем этот список vX. Теперь просто можно обработать операцию добавления числа в G. Пусть добавляемое число — это X. Добавим число X в список G. Пусть i — позиция добавленного числа в список G.
Теперь давайте добавим позицию i в список vX.
Можно заметить такой факт:
Если размер списка vx равен 4, то мы нашли нужную нам четверку.
Можно заметить ещё один факт:
Если до добавления мы не нашли нужную четверку чисел, а после добавления нашли, то последнее добавленное число является последним в четверке. То есть наше последнее добавленное число равно c4. Значит мы знаем позицию последнего числа из четверки. Давайте переберем позицию числа c2. Всего возможных позиций числа c2 не больше двух, так как всего позиций, на которых стоит число c2, не больше трех (смотреть предыдущий факт). Одна позиция уже занята числом c4. Итого остается максимум две позиции. Пусть мы проверяем, то что c2 имеет позицию L, а c4 имеет позицию R. Остается только проверить существование таких c1 и c3, что c1 = c3 и их позиции P и Q соответственно. P и Q должны удовлетворять следующим условиям: 1 < P < L, L < Q < R. Это очень легко проверить. Давайте заведем массив T. Ti = максимальное j, что Gi = Gj. Поддерживать такой массив не составляет труда. Теперь проверка будет требовать только одного запроса: Максимум на отрезке [1, L - 1] в массиве T. Пусть результат запроса равен Z. Если он удовлетворяет условию L < Z < R, то четверка существует. Этим запросом мы нашли позицию числа c3 в списке G. По этим данным мы можем восстановить четверку.
Чтобы найти максимум на отрезке за  , можно воспользоваться деревом отрезков или деревом Фенвика.
, можно воспользоваться деревом отрезков или деревом Фенвика.
Итоговая асимптотика: 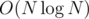 .
.











There's also a nice and short solution for E which uses only stack and map/dictionary, check my implementation — 7902705. The idea is taken from enesoncu's code
Since this was in Russian, I don't think proper discussion happened on this one, so can someone propose a better solution for D?
Can someone explain the solution to question C in English clearly? I think google translate messed up the translation.
To those who need it: Hint: use dp with states k, n.
Tutorial: The first thing to notice is that each interval needs to be of length m. The thing that strikes is to: First, build an array where the jth element stores the sum of the elements. Now, you can be greedy. choose the interval with the largest sum, then the next non-intersecting interval with the largest sum and so on. But this won't ensure that all k intervals are used. So greedy doesn't work.
So the solution must be dp. The states are n, k. I tried using n as first and k as second states: I found k as first is better.
Now, dp[k][n] is going to be max of: dp[k-1][n-m] + sum of interval ending at n = sum[b] and dp[k][n-1].
This because at each point you can either ignore the interval. Or you can choose it, and then avoid m next points. Because intervals of these points will intersect with the chosen point's interval. At each point, you want the maximum of the two options.
The answer is at dp[k][n].
Code: 75654562
Can you explain where greedy would fail?
i am still a beginner and this is my first comment.hope you can understand. Greedy fails in test cases where by choosing an interval of(l,r) of highest sum you are left with no other interval that you can possibly choosefrom!
eg-test case->
u will choose the (1,2)[array indexed 0] but further you cant choose the other pair.There might be a lot of cases similar to this.Hope you understood
but in that test case it does not matter because we just need to answer the sum...so it will adjust itself...so i think greedy can work
Thanks!
How to remove TLE in the following python code for Problem C. George and Job
LINK
My solution for problem E:
We look for a maximal subsequence that looks like x1 y1 x1 y1 x2 y2 x2 y2...
Let's denote the indexes of elements of some valid grouping as A, B, C, D
Let nxt[i] be the next appearance of a[i] after i (if it doesn't appear set it to be index n (one after the last index))
The main observation:
Claim: If there exists an optimal solution in which we use A = i, then either there exists an optimal solution in which C = nxt[i] or there exists an optimal in which we don't use i, (therefore when considering i we can always pair to nxt[i]) Proof: suppose A = I we chose some C > nxt[i], then there are 2 cases: if B < nxt[i] then we can just use C = nxt[i] to get the same answer. if B > nxt[i], then there exists an optimal solution in which we don't have to use i (namely, let A = nxt[i]) hence we proved the claim.
now, let dp[i] be the length of the best subsequence of the array [i..n-1] divided by 4 (number of groups) then dp[i] can be dp[i+1], or either 1 + dp[D+1] if there exists some (A, B, nxt[A], D) in which A = i and it's valid and out of all of those we trivially choose the one with minimal D because the dp when going from index n-1 to 0 is non-decreasing.
now the task is the following: for A = i, determine if there exist valid (B, nxt[A], D) and out of all of them find the one with minimal D.
we need one more observation: the answer is the minimum value bigger than nxt[A] in the range [A+1, nxt[A] — 1]. Hence we can use persistent segment tree/sweep line + regular segment tree to compute the answer.
▀
Note: Please note that you might need to consider groups like x, x, x, x separately. (just min ans with this option)
In problem 467C - Юра и работа you don't even need to precompute prefix sums, since it is guaranteed that $$$m \cdot k \le n$$$, and hence $$$O(nmk) = O(n^2)$$$. There is almost no runtime difference between 245705653 (prefix sums, 186 ms) and 245706424 (naive loop, 187 ms).