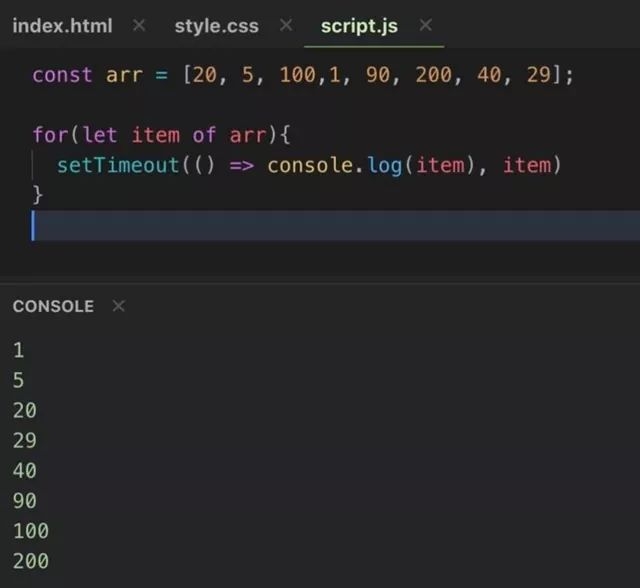
For an array $$$a$$$, $$$A = \max(a)$$$.
Could such a thing actually be made to be more efficient than normal sorting algorithms?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 166 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
For an array $$$a$$$, $$$A = \max(a)$$$.
Could such a thing actually be made to be more efficient than normal sorting algorithms?

| Название |
|---|



I think you can even make it $$$O(n + \log A)$$$ if you set the timeouts as $$$\log(a_i)$$$ instead of $$$a_i$$$.
why stop there: use inverse-ackerman instead of log
Look up counting sort.
That's counting sort
so if it is a known thing and not just from some guy on r/programmingHorror's web project, why isn't it used as $$$the$$$ sorting algorithm?
It is used sometimes probably, the thing is that it's easier to type .sort() than write this. And it won't add much to solution's complexity
Because it uses $$$O(A)$$$ additional memory, not necessarily something you would want. And when $$$A$$$ is large, this becomes inconvenient.
We might be able to optimize it to $$$O(\log A)$$$ additional memory (see my above comment).
Cause if the upper bound of array elements is $$$O(n^2)$$$ the complexity would be $$$O(n^2)$$$ regardless of n. It can be used in some special scenarios.
By "regardless" I just mean it's dominated by the other term That was a silly thing to say Sorry :)
Look up "Sleep Sort" precisely
Hacked.
I think a better implementation would go like this:
Create $$$n$$$ threads, $$$1$$$ for each element in the array (don't start the threads yet).
Go through each thread, very quickly starting them one after the other, so we don't run into the time error.
To really make sure we don't run into the time error, we can first sort the threads by the value of the element they contain in ascending order so that when we start thread $$$b$$$ after thread $$$a$$$, the value of $$$b$$$ will surely go in after the value of $$$a$$$ because it is larger.
That is brilliant! If we sort the threads by the element they contain, we can further optimize it by replacing all setTimeout(_, x) calls with setTimeout(_, 0), since surely the earlier threads will still finish first. In fact, as an even further optimization, since the sleeping is redundant now, we can skip creating the threads and timeouts as well! Now, the only thing we have left to do is find an efficient sorting algorithm.
If you want $$$O(n + A)$$$ sorting, you can just use counting sort. Your time based sorting is almost certainly strictly worse, since for large $$$n$$$, the processor still has to use some algorithm to determine when to wake each thread, which is likely done using something equivalent to counting sort with worse precision or a priority queue.
high IQ
That's what I'm saying. Who even thinks of this? It's such out of the box thinking imo. It reminds me of that one short film on youtube where everyone's head explodes when they hear an original idea. This is kind of like that, because this is an original idea in my opinion.
I just don't think cf problems test the same thing coming up with something like this tests. It might be like IQ vs some sort of creativity or something.
How about making the timeout $$$\frac{1}{item}$$$, and once sorted, based on this timeout, you could just reverse the final array, since then the sorting time would be the least,even less than $$$log$$$ and inverse-ackerman, assuming all the numbers are greater than equal to 1. Also like you said, once you include multithreading, there won't be any problem related to error in the solution.
The only restriction would be that we can not take the numbers less than equal to zero, one solution to that could be to sort the negative numbers separately by taking their absolute value, and then merging the final arrays and placing all the zeroes in between.
By the way pretty intresting sorting algorithm XD. Let's see how much time it takes me to get an AC with this method XD.
296356256
It seems python is too slow for this algorithm :/. In case anyone could optimize it, do let me know
lol what I figured out is that it is way too slow for that problem. Also, the fact that $$$k$$$ goes up to the huge number $$$10^7$$$ makes it so the algorithm will incorrectly sort a lot of the cases. I tried to solve it with the threading module, but I ended up basically copying your implementation of the algorithm when the threading failed.
It turns out that python isn't even fast enough to process $$$1000$$$ elements per second. So I had to go back and find a $$$div. 2 A$$$ that had really tiny constraints. Luckily, I found this one with one case per test, $$$n \le 100$$$, and $$$a_i \le 1000$$$. Still, I had to binary search the proper amount of time to sleep for, since if I slept for too little time, I'd get WA due to wrong sorting, and if I slept for too long, I'd get idleness limit exceeded. Finally, I got an accepted submission.
Also, I think the problem with sorting by $$$\frac{1}{a_i}$$$ is that there are too many sorting errors, especially as $$$a_i$$$ gets higher and higher. But actually that would, in theory, be an $$$O(n)$$$ sorting algorithm lol
tl;dr: the time complexity of this sorting algo is a bit misleading
damn, saw your submission history, respect for the dedication 🫡
there is a way to save the sort elements in js with that method?
If the smallest precise measurable time in a computer is < 1 ns and we have unlimited CPU cores, then we can sort 1e9 elements within the integer range in 1 second.
Took so much time
Using log(time) is fast, still it takes more time then expected
It's all good until we have negative values
We can add an offset number for minimum negative value and use the absolute minimum negative value to convert numbers in positive and get actual numbers by substracting that offset number.
The cost of getting faster time compilation is compensated with more memory I guess.
This sort is quite incorrect
Radix sort or counting sort maybe?
CLRS has a nice chapter on such algorithms It's chapter 8 (titled "sorting in linear time") if i'm not mistaken. Check it out if you're curious