Hey guys,
Recently I faced an interesting problem which took me about couple of days of thinking but I couldn't find out the polynomial time solution. So I decided to share it with you:
Let
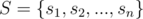 0 ≤ si ≤ 3
0 ≤ si ≤ 3
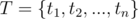 0 ≤ ti ≤ 1
0 ≤ ti ≤ 1
Now we want to Change the elements of S in a way that the following conditions are fulfilled:
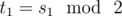
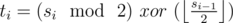 2 ≤ i ≤ n
2 ≤ i ≤ n
The only operations allowed are to increase or decrease si by 1 or let it to be unchanged. The goal is to find the minimum number of increasing or decreasing operations which satisfy the above equations for S and T. This task can be simply done using the Dynamic Programming in O(n) for any given S and T.
The main Problem is "what is the expected value of minimum operations for every given n?". The first Idea is to generate every Sequence of S and T for a given n, after computing the minimum operations for each pair, calculate the expected or average value. but this runs in O(n8n). Is there a polynomial time algorithm like DP for solving this task?











It appears your problems stem from not thinking carefully about the original problem. Sure, it can be solved in O(n) using DP, but you need a simpler solution than that.
Try to prove that the following greedy algorithm works: whenever you are forced to change an element si and 1 ≤ si ≤ 2, change it so that si + 1 does not need to be changed.
From here, it should be easy to use DP to solve the full problem. I'm leaving the details as an exercise for the reader.