ASHWANTH_K's blog

Segment tree for graph problems
By ASHWANTH_K, history, 13 days ago, In English
  • Recently I came across a new idea to solve graph-related problems using segment trees, I would like to discuss the same with a problem.

Problem:

Given a graph $$$G$$$ with $$$N$$$ nodes and many edges (around $$$O(N^2)$$$), Goal is to perform the Dijkstra algorithm on this dense graph and find out the shortest path cost from node 1 to all other nodes.

The edges are given in a compressed format. The input follows $$$M$$$ lines. Each of the $$$M$$$ lines consists of 4 integers U Lx Rx C meaning there are edges from node U to all other nodes in range [Lx , Rx] with cost C. Edges are uni-directional.

Example:

For N = 6 , the edge-group U = 1 , [Lx,Rx] = [3,5] , C = 10 looks like:

Constraints:

  • $$$1 \le N \le 10^5$$$
  • $$$1 \le M \le 10^5$$$
  • $$$1 \le U \le N$$$
  • $$$1 \le Lx \le Rx \le N$$$
  • $$$1 \le C \le 10^9$$$

Do spend some time thinking about this problem, before proceeding to the solution.

Initial Thought Process:

  • The main problem faced here is that in the worst case, we have plenty of edges $$$O(N^2)$$$, performing Dijkstra in this dense graph would lead to time complexity $$$O(N^2 log(N))$$$ which would give TLE. Also, it is not possible to store all edges in the adjacency list, giving MLE.

  • So we need to seek out some ways to reduce the number of edges so that time complexity can be improved.

  • Our solution proceeds like this, first we try to convert this dense graph to a sparse graph with less number of edges and then perform the Dijkstra Algorithm to find our answer.
  • Since the input of edges is also given in compressed format, intuitively we can think that there might be some ways to represent a group of edges as a single edge, so that we can reduce the number of edges and solve our problem.

Solution: Segment Tree as a structure

  • One main observation in this problem is that we add edges from node U to a range of nodes [Lx, Rx]. This gives an intuition that we deal with ranges and we can use segment trees to solve our problem.
  • In our solution, We only use the structure and ideas of segment tree (complete binary tree). We dont calculate or store anything in the segment tree nodes.
  • First, we build a segment tree $$$G'$$$ with $$$N$$$ leaf nodes, ($$$2N$$$ nodes in total). These $$$N$$$ leaf nodes represent the $$$N$$$ nodes of the original graph $$$G$$$ and add edges from parent to its left and right children with 0 cost.

Example N = 8

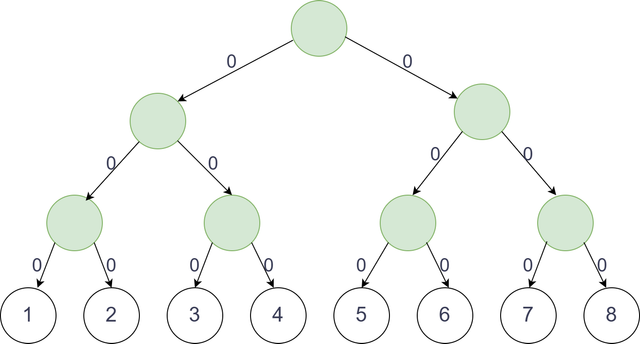
  • It is a well known fact that any range [Lx , Rx] can be covered by $$$O(log(N))$$$ nodes in a segment tree. So for every edge-group U Lx Rx C, we add edges from node U to these $$$O(log(N))$$$ nodes with cost C.

Example: N = 8, U = 1, [Lx,Rx] = [3,8], C = 10

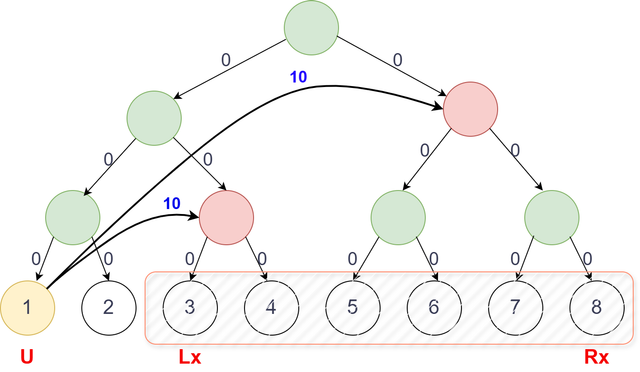
  • Since from any intermediate node, we can visit the leaf nodes in its subtree with 0 cost, this graph $$$G'$$$ preserves the same information of graph $$$G$$$.
  • Total number of edges is $$$2N$$$ (intial graph) + $$$M*logN$$$ (for each edge-group), So total edges are $$$E = O(Mlog(N))$$$.
  • Performing dijkstra in this graph $$$G'$$$ would give time complexity $$$O(Mlog^2(N))$$$ which would pass under the given constraints.

Problems using this idea:

  • Vote: I like it
  • +169
  • Vote: I do not like it

»
13 days ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Am I misunderstanding the problem or is it trivial to solve it in $$$O((n + m) \log{n})$$$ with $$$O(n + m)$$$ memory instead:

  • Create segment tree of size $$$n$$$, element $$$i$$$ represents node $$$i$$$. Initialize it with all values set to $$$\infty$$$ and the value of the source node set to $$$0$$$ (value represents distance).
  • Run $$$n$$$ iterations of the following loop:
u = index with min value
d = val[u]

for all outgoing edges [u, l, r, c]:
     perform range update on [l, r], val[i] = min(val[i], d + c)

set val[u] to some value such that it wont be returned as u in any other iteration (effectively toggling "off" its leaf node in the segtree)
→ Reply
  • »
    »
    13 days ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    How are third type updates handled?

    → Reply
  • »
    »
    13 days ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think you can probably do that, it's arguably a bit more difficult to code though, and you would have to maintain in each node how many nodes in it's subtree are toggled and how many are not. Also, the trick with weighted edges between different nodes inside a segment tree is really elegant in my opinion, so it was nice to see.

    → Reply
  • »
    »
    13 days ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yes, you are correct, we can store distances in a segment tree and build a min segment tree with lazy propagation. But this works only for this problem. I don't think that the practice problems can be solved with this strategy, I intended to just introduce this idea in a blog and felt this to be very elegant solution. But yeah other solutions exist.

    → Reply
    • »
      »
      »
      13 days ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      The practice problem can also easily be solved in this manner, by just creating one more segment tree to handle type 3 queries 289128975.

      → Reply
»
13 days ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks

→ Reply
»
13 days ago, # |
  Vote: I like it +13 Vote: I do not like it

Nice blog! Here are some othe problems I've found that use this technique: Golf, Passport

→ Reply
»
13 days ago, # |
  Vote: I like it +19 Vote: I do not like it

Another problem on this idea which I've seen ages ago (and still looking for some judge to be able to submit, if someone knows it, pls help).

$$$N$$$ mines are positioned on a line, each has its coordinate $$$x_i$$$ and radius of explosion $$$r_i$$$. When some mine explodes, all other mines in its radius explode. Then they can explode other mines and the chain reaction happens. Find for each mine the number of mines that will explode if you explode this manually. $$$N\leq 10^5, |x_i|, |r_i|\leq 10^9$$$.

Also this idea can be done on trees, you'll need centroid decomposition. A nice example is All-Russian Olympiad 2015, problem 8 (I don't think it exists on CF, here is the link to Russian statement)

→ Reply
»
13 days ago, # |
← Rev. 2   Vote: I like it +48 Vote: I do not like it

Yeah, it is a cool trick! I love it! So this makes a graph with $$$O(n)$$$ vertices and $$$O(n + m \log n)$$$ edges. Instead of a segment tree, one can also build a sparse table (disjoint if needed) on top of the vertices to get $$$O(n \log n)$$$ vertices and $$$O(n \log n + m)$$$ edges. It could be advantageous if $$$m » n$$$. Basically, it's the same idea. But when I saw it in the context of sparse tables, I understood how general it could be.

→ Reply
»
12 days ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem: 1602D - Frog Traveler
Solution: 133095322

→ Reply
»
12 days ago, # |
  Vote: I like it 0 Vote: I do not like it

Wow!!! I rally like your idea to represent range of nodes as a node of segment tree. Very nice ways of problem solving

→ Reply
»
12 days ago, # |
  Vote: I like it -20 Vote: I do not like it

thanks, i hope i reach pupil after this blog.

→ Reply
»
11 days ago, # |
  Vote: I like it +8 Vote: I do not like it

This is a really nice idea. I remember seeing it at our IOI preparation last year and I am really happy that I was able to come up with it myself while solving problem CSA — Field Activation (in 1 dimension).

Another great example of the idea is

EGOI 2023 Problem
→ Reply
»
11 days ago, # |
  Vote: I like it 0 Vote: I do not like it

I've been struggling with B — Legacy for a really long time, and now i come across this blog. What a saviour of my life ! Thanks

→ Reply
»
11 days ago, # |
  Vote: I like it 0 Vote: I do not like it

Here is another source mentions this technique:

https://robert1003.github.io/2020/02/14/graphs-and-segment-tree.html

→ Reply