cancaneed's blog

Bounded tuples(need help)
By cancaneed, history, 5 weeks ago, In English

Bounded tuples

  • Vote: I like it
  • +17
  • Vote: I do not like it

»
5 weeks ago, # |
  Vote: I like it +5 Vote: I do not like it

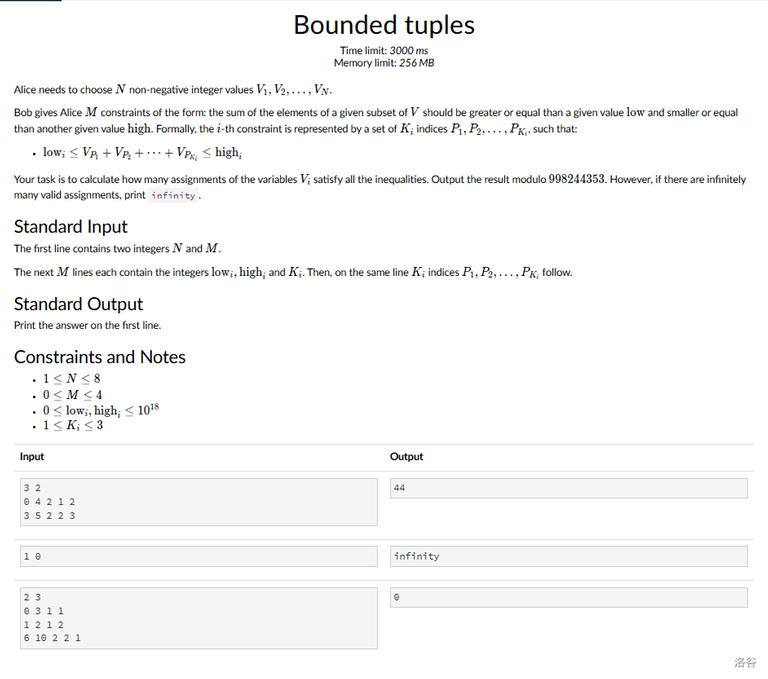
It seems like a very constrained version of the "count integer points inside a polytope" problem. For fixed dimension there are polynomial solutions for it. See: A Polynomial Time Algorithm for Counting Integral Points in Polyhedra When the Dimension Is Fixed [AI Barvinok · 1994].

I don't know for sure, but possibly you can maybe simplify this paper a bit and just implement that. Still that seems really hard. I don't know if there's any easier ideas.

→ Reply
  • »
    »
    4 weeks ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thx, I’ll give the paper a read. appreciate your help here!

    → Reply