Submission Хочется рассказать о логике, использованной при решении задачи Е (которую я не успел дописать за отведенное время и засабмитил на дорешивании).
Для этого пригодится знание того, что такое числа Каталана, а также как умение выводить их формулу. Подробно про числа Каталана можно прочитать, например, на вики: тык, Можно по разному дать определение, мы определим число $$$C_n$$$ как количество правильных скобочных последовательностей длины $$$2n.$$$ Нас интересует следующий довольно известный и изящный метод найти это число.
Рассмотрим координатную сетку, по которой нам нужно дойти из угла $$$(0,0)$$$ в угол $$$(n,n)$$$. Мы можем идти только вправо или вверх. Шаг вправо соответствует открывающейся скобке, шаг вверх — закрывающейся. Тогда существует взаимно однозначное соответствие между правильной скобочной последовательностью длины $$$2n$$$ и путем из $$$(0,0)$$$ в $$$(n,n)$$$, не пересекающим диагональ $$$y=x$$$, так как точка выше этой диагонали означала бы что на данном префиксе закрывающихся скобок больше чем открывающихся. Как найти количество таких путей?
Количество всех путей равно $$$\binom{2n}{n}.$$$ Из этого числа мы вычтем количество неправильных путей. Неправильные пути — те, что пересекают $$$y=x$$$, или, что эквивалентно, имеют хотя бы одну общую точку с прямой $$$y=x+1.$$$ Возьмем первую (с наименьшим $$$x$$$) общую точку $$$(a, a+1)$$$ и отразим участок пути от $$$(0,0)$$$ до $$$(a, a+1)$$$ относительно прямой $$$y=x+1.$$$ Получим некоторый путь из $$$(-1,1)$$$ в $$$(n,n)$$$. Это — взаимно однозначное соответствие. Действительно, любой путь из $$$(0,0)$$$ имеющего общие точки с $$$y=x+1$$$ можно отразить до первой такой точки. В то же время любой путь из $$$(-1,1)$$$ в $$$(n,n)$$$ обязан иметь общие точки с $$$y=x+1$$$, так как начало и конец пути расположены по разные стороны от прямой, а значит мы также можем отразить кусок пути до первой такой точки. Количество таких неправильных путей — $$$\binom{2n}{n+1}.$$$ (или. эквивалентно $$$\binom{2n}{n-1}.$$$) А значит количество правильных путей $$$C_n = \binom{2n}{n} - \binom{2n}{n+1}.$$$ Это и есть число Каталана. Подробнее на картинке. 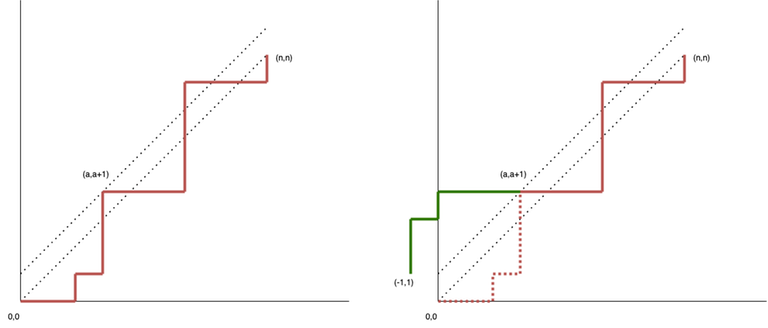
Если бы в задаче не было козырной масти, выигрышное распределение карт между игроками удовлетворяло бы условию что все карты одной масти распределены в порядке правильной скобочной последовательности, по $$$m/2$$$ карт у каждого игрока. Однако наличие козыря потребует от нас двух модификаций для формулу выше.
Во-первых, масть 1 по-прежнему должна удовлетворять условию префикса правильной скобочной последовательности, однако она не обязана быть оконченной. Любой путь из $$$(0,0)$$$ в $$$(a, m-a), a \ge m-a$$$, не пересекающий $$$y=x$$$ удовлетворяет условию. Количество таких путей $$$\binom{m}{a} - \binom{m}{a+1}$$$. Такое распределение мастей оставит нам $$$2a - m$$$ козырей, которые мы можем потратить на дальнейшие масти. Это будет базой нашего ДП. Пусть $$$dp_i[ta]$$$ — количество способов расположить выигрышным образным первые $$$i$$$ мастей, оставив в запасе $$$ta$$$ козырных карт. Тогда $$$dp_1[2a - m] = \binom{m}{a} - \binom{m}{a+1} \forall a \ge m/2.$$$
Во-вторых если мы тратим на масть $$$i \ne 1$$$ $$$k$$$ козырей (это число может быть только четным), это означает что игрок 1 выкладывает $$$(m - k)/2$$$ карт масти $$$i$$$ а игрок 2 — $$$(m+k)/2$$$ карт. При этом карты должны удовлетворять условию "не слишком неправильной" скобочной последовательности, а именно, на любом префиксе количество закрывающихся скобок не должно превышать количество открывающихся больше чем на $$$k.$$$
Соединив эти мысли, получаем что результат — количество путей из $$$(0,0)$$$ в $$$(\frac{m - k}{2}, \frac{m + k}{2})$$$, не пересекающих $$$y = x + k$$$. Плохие пути отражаются аналогичным образом, но относительно прямой $$$y = x + k + 1$$$, в пути стартующие в $$$( -(k+1), (k+1))$$$. Таким образом количество хороших путей $$$f(m,k) = \binom{m}{(m - k)/2} - \binom{m}{(m - k)/2 + k + 1}$$$. 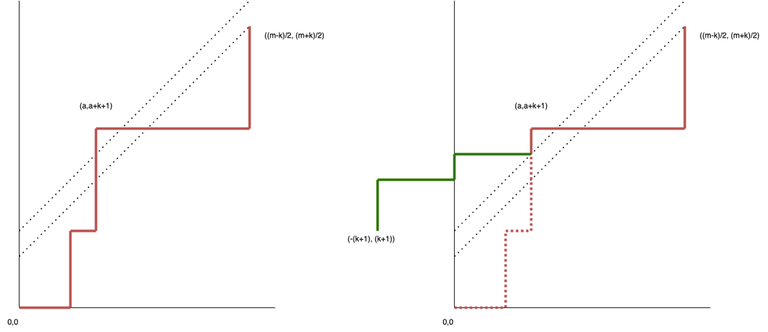
Сам переход ДП несложный: $$$\forall ta \le m, \forall k \le ta, dp_i[ta - k] += f(m,k)*dp_{i-1}[ta].$$$ Достаточно итерироваться только по четным $$$ta$$$ и $$$k$$$. Ответ $$$dp_n[0].$$$ Сложность $$$O(m^2n).$$$










The derivation for Catalan numbers is simply amazing, never though it could be explained this way. Next time I need to derive $$$C_n$$$ this will definitely be the first thing that comes to my mind. Thank you so much for the insightful blog.
Тут выявлен обобщеный случай(с тремя переменными)
This distribution of suits will leave us with 2a - m trump cards that we can use for other suits.Sorry if I am wrong, but shouldn't this be
m-2a?No, it's $$$2a -m$$$. If player 1 has $$$a \ge m/2$$$ trump cards, player 2 has $$$m - a$$$ cards, so after matching player 1 left with extra $$$a - (m-a) = 2a -m$$$ trump cards.
Please add this link. If anyone has still problem understading the visualisation, this video might help ...
https://www.youtube.com/watch?v=kaInaIUABzY
very nice explanation , but why is it that when u reflect a path u only reflect on the first intersection point ? reflecting the whole path on the line will give the same result
edit : actually reflecting the whole path does absolutely nothing ignore the above comment