Как искать К-ую порядковую статистику на отрезке используя НЕ ПЕРСИСТЕНТНОЕ дерево отрезков. И вообще, возможно ли это?
UPD: ссылка на задачу — http://www.e-olimp.com.ua/ua/problems/3866
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
Как искать К-ую порядковую статистику на отрезке используя НЕ ПЕРСИСТЕНТНОЕ дерево отрезков. И вообще, возможно ли это?
UPD: ссылка на задачу — http://www.e-olimp.com.ua/ua/problems/3866
| Название |
|---|



Возможно.
Бинпоиск по ответу. В функции-проверке будем подсчитывать количество чисел меньше проверяемого. Для этого в каждой вершине ДО будем хранить отсортированный кусок массива и запускать бинпоиск по нужным кускам. Итого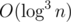 на запрос. Как раз под ограничения задачи.
на запрос. Как раз под ограничения задачи.
Если еще в вершине для каждого элемента в отсортированном списке хранить индекс большего по величине в левом и правом сыновьях, то второй бинпоиск не нужен (индекс можно пересчитывать в спуске), получается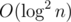 на запрос :)
на запрос :)
MrDindows, получается нужно чтобы в бин. поиске(который по ответу) рассматривались только числа которые есть на текущем отрезке. Как это сделать?
Явно хранить их в отсортированном виде в вершине.
Та это понятно. Только вот такой тест: 5 2 6 3
Найти на отрезке 1..4 3 элемент.
Если искать это бин. поиском то может оказаться что ответ 4, но 4 на отрезке нет. Надеюсь понятно написал о чем думаю.
Ну можно попутно в каждом подотрезке найти lower_bound найденного значения и выдать ответом минимум из этих чисел.
Если считать количество чисел не строго меньше, а меньше либо равно, то будет классический бинпоиск.
MrDindows, имелось ввиду что бин. поиск может найти такое число которого нет на отрезке!
Можно заметить, что тот вариант бин. поиска, который он описал найдёт как раз то, что нужно, если внимательно его изучить.
adamant, я не понимаю, почему именно этот бин. поиск должен работать(не находить число, которого нет на отрезке). Можете обьяснить?
Этот бин. поиск находит первое число, для которого количестве элементов, меньше либо равных ему равно k. Так как foo(x)>foo(x-1) только у чисел, которые существуют в множестве, то и остановиться мы можем только на таком числе.