Xellos's blog

TC SRM 629: A solution for div1 950pt
By Xellos, 10 years ago, In English

This was originally intended as an answer for this comment, but eventually I realized that it's too long (also, the Preview feature takes way too long to process it), so it's a blog post instead.

This has complexity of 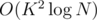and a horrible constant. If there's a better solution, write it in the comments.

UPD: KADR provides a solution using polynomial interpolation in O(K2).

Problem statement

There are N boxes numbered 1..N; box number i contains i candies and 1 stone. We pick 1 random object from each box. Calculate 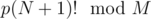, where p is the probability that K of these N objects are candies.

Constraints: 1 ≤ K ≤ N ≤ 109, 2·109 ≥ M ≥ 109 and M is prime.

Solution

It's clear that since the probability of picking a candy from box k is 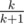and the probability of not picking one is , the answer is (Sn denotes the set )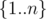

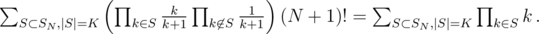
Let's denote this sum as P(N, K) and introduce another sum (N / 2 is integer division)

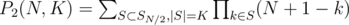
which calculates the same sum P(N, K), but with an additional restriction that S can only be subsets of range .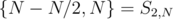

If that restriction was instead that S can only be subsets of range , the sum would obviously be just P(N / 2, K).

Also, let's denote .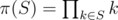

Naive solution

If the constraints were small, we could use simple DP on P(N, K). If we don't use N in S, then we sum up π(S') of the same subsets S' as in P(N - 1, K). If 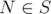, we only need K - 1 elements from the range SN - 1, so we sum up π(S) = Nπ(S') of the same subsets S' as in P(N - 1, K - 1).

This runs in O(NK) and would obviously give TLE. What we can do instead is splitting the range SN into 2 halves of size N / 2 (and possibly 1 integer N / 2 + 1 in the center for odd N).

Calculating P(N, K) — even N

Suppose we knew how to calculate P2(, ) already. In order to calculate P(N, K) for even N, we can split any disjointly and uniquely into 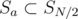and .

If |Sa| = i, then |Sb| = K - i; any 2 sets Sa and Sb can be merged to form one set S and so we have for fixed i

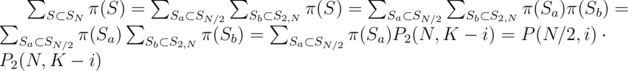
Since i can be any integer in [0, K], we get

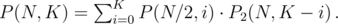
Calculating P(N, K) — odd N

In this case, we can again split S disjointly and uniquely into Sa, Sb as above and another set 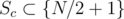. We have 2 choices for Sc: either it's empty or contains N / 2 + 1; if it's empty, then we get the same sum as for even N.

If Sc is non-empty, we can again use that π(S) = π(Sa)π(Sb)π(Sc) = π(Sa)π(Sb)(N / 2 + 1), where we can take N / 2 + 1 out of the sum and get a similar sum as for even N — the only change is that if |S1| = i, then |S2| = K - 1 - i and

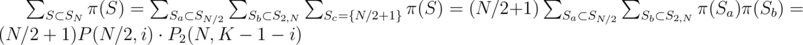
Again iterating over all i from 0 to K - 1, we get a formula for odd N:

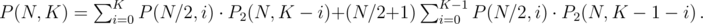
Calculating P2(N, K)

Let's expand the sum as

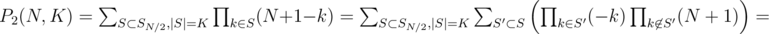
It's clear that if |S'| = K - i, then

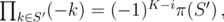
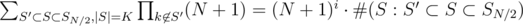
where 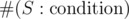denotes the number of sets S (of size K) satisfying the condition.

How to count that number? We can just exclude set S' from all S and SN / 2 (since they all contain S'); then, we can see that we just need to count the number of subsets of SN / 2\ S' of size i. That's obviously just 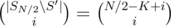, so

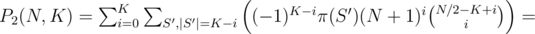
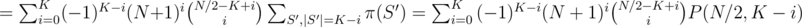
Binomial coefficient

The binomial coefficient has kinda big arguments, no? We can't just pre-compute a Pascal triangle or factorials, but i is sufficiently small, so we can just use one of the most basic formulas for binomial coefficients

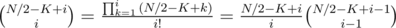
and so, for given N, K, compute the necessary binomial coefficients along with corresponding terms in the sum for P2(N, K). It's useful to have modular inverses precomputed; here, we can use that M is a prime larger than K, so by Fermat's little theorem, .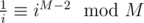

Complexity

We now have a fairly simple way to compute P(N, K) and P2(N, K) in O(K) time with some pre-computation. The important thing is that thanks to integer division, the N in the argument can only be N from the input divided by powers of 2; since there are just such powers that don't lead to the trivial case N = 0, and with fixed N, we only spend O(K2) time on computing P() and P2() for all possible K, the complexity is .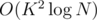

The limits are too tight, though — the biggest problem is there are a lot of modulos that take a lot of time. One possible improvement is only taking the modulo when computing the sums for P() and P2() after every 4 additions, that gives me worst-case runtime of around 2.1 seconds (so close TLE T_T). Also, we can precompute 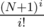, which saves us some modulo operation compared to precomputing (N + 1)i and 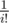separately. Code

  • Vote: I like it
  • +60
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 2   Vote: I like it +27 Vote: I do not like it

There is one small optimization about modulos that can reduce the runtime a lot.

Suppose we have to compute something like this (here 0 ≤ ai, bi < MOD and MOD < 231):

long long res = 0;
for (int i = 0; i < n; i++) {
    res += a[i] * b[i];
    res %= MOD;
}

The trick is that we can compute the sum modulo MOD2 without modulo operations itself:

long long res = 0;
for (int i = 0; i < n; i++) {
    res += a[i] * b[i];
    if (res >= MOD * MOD) res -= MOD * MOD;
}
res %= MOD;
→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +5 Vote: I do not like it

    Yes, that's one of many things I tried — but didn't get a noticeable increase in speed.

    UPD: I played with it a bit more and what works is combining the 2 tricks — when I take A[][] and A2[][] modulo , I can afford to check for subtraction only on every second addition:

    if(i&1 && A[s][j] >= 2*modSq) A[s][j] -=2*modSq;

    and this gets AC in less than 1.95 seconds worst-case runtime.

    UPD2: This is still a bit labile, since swapping arguments in the if() results in runtime close to 2 seconds and possible TLEs (when very unlucky). But it's still nothing compared to how worse the runtime gets when moving the line decP =(decP*((N>>(s+1))-j+i+1))%mod; (btw this one takes about half of the whole runtime).

    → Reply
»
10 years ago, # |
  Vote: I like it +77 Vote: I do not like it

There is another O(K2) solution that involves interpolation. First, one can notice that the answer can be calculated using the following recurrence relation:

f(N, K) = N·f(N - 1, K - 1) + f(N - 1, K)

Another observation is that f(N, K) is a polynomial of N of degree 2K. This can be proven by induction (although I didn't try to do this during the contest). So we can calculate f(i, K) for i from 1 to 3K + 1 using the above formula and then use f(K, K), f(K + 1, K), ..., f(3K + 1, K) as the values of our polynomial p(x) in points K, K + 1, ..., 3K + 1. Interpolation can be done in O(K2). Finally, the answer to the problem is p(N).

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Very good solution. But how you observe this fact?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well, it was just guess based on the general look of the formula and on the fact that K is small.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I did not understand why f(N, K) 's degree is 2K not K.

    Let p(N, K) degree of f(N, K). Then p(N, K) = max(1 + p(N - 1, K - 1), p(N - 1, K)) right?

    Could you tell what did i miss?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Consider a simpler formula:

      f(0) = 0
      f(N) = N + f(N - 1)

      According to your logic p(N) = max(1, p(N - 1)) = 1, which is false.

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      So,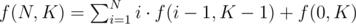 and f(0, K) = 0 (K > 0). Suppose that 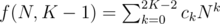, which holds for K - 1 = 0; then

      where the inner sum is something like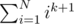 , which is known to be a polynomial of degree k + 2. Picking k = 2K - 2, we get that f(N, K) is a polynomial of degree 2K.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Which algorithm you use for polynomial interpolation? Do you have a reference for implementing it in C++?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      Shouldn't straightforward Lagrange be sufficient? It's basically "copy formula from Wikipedia if you don't remember it".

      And it works in O(degree2).

      → Reply
»
10 years ago, # |
  Vote: I like it +24 Vote: I do not like it

It is surprising for me that this problem is exactly the same as a problem which I set up 2 years ago.

problem link ( In Chinese

That time my proposed solution is O(k^2) with fascinating application of Principle of Inclusion and Exclusion. But some people came up with O(k^2logn) approach (which can be speed up to klogklogn by FFT)...

I have write a solution for that problem that time and give the insight of the this problem, Unfortunately it is in Chinese :( link

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    The solution seems to be similar to mine (based on what I could guess from the formulas). What's the idea behind your O(K2) solution?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Use Inclusion and Exclusion we can turn this problem in to counting the number of n vertices connected graph with odd or even edges...

      Actually, those constraints are (i and j should not be the same), so if we flip it then we should let (i and j is the same), we can do it by connect i and j with an edge, then a connected component of a graph should be the same, and the number of the edge is the number of flip we have made, base on whether it is even or odd, we add or subtract it.

      If k vertices are the same, what we want is \sum_{i=1}^{n} i^k , which can be calcualted by some formula.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I saw this formula for Sterling numbers of first kind. http://upload.wikimedia.org/math/e/4/7/e47bc8bab37c7a86cc15eb5ecef53f5c.png This formula works in O(K*K), but it might give 0 when take modulo with MOD due to (2n-m) factorial.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    But it seems to me that it works in O(N2) what we need to compute is s(N, K).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Won't S(n+1,n+1-k) give the answer, which can be computed in O(K*K).

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, right. The recurrence is a bit different.

        It's strange that this formula gives a polynomial in K, not in N... but it should work.

        A more relevant question about the factorials is: how do we compute huge ones? If 2n - m is just a bit smaller than the prime modulo, we can't compute it iteratively because of time (and memory) limits.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 5   Vote: I like it 0 Vote: I do not like it

          For S(n, m) we need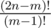 which in case of S(n + 1, n + 1 - k) will be 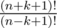which can be done in O(k).

          All other factorials similarly won't exceed O(k), IMO.

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Well, that means we don't need to care about the factorials being divisible by the modulus, since we don't need modular inverses there — just multiplication.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Yes, but for n + k + 1 exceeding MOD, it'll always evaluate to 0 and that was the initial problem that I had faced in solving this problem.

              → Reply