kien_coi_1997's blog

How to solve this hard problem about sequences?
By kien_coi_1997, 10 years ago, In English

There is a integer sequence a[1]..a[n] (some of them could be negative). We have to do m following queries:

Choose a consecutive sub-sequence a[L..R], with two positive number x and y, perform following operators: increase a[L] by x, increase a[L+1] by x+y, increase a[L+2] by x+2*y, ... increase a[R] by x+(R-L)*y.

Suppose that after kth-query, a[i] become non-negative, then Answer[i]=k. In other words, F[i] = how many queries have been done to make a[i] become >= 0. Additionally, if initialy, a[i]>=0 already, Answer[i]=0. If after m queries, a[i] is still negative, Answer[i]=-1.

Input contains n, a[1..n], m, and m queries, each query have 4 integer L, R, x, y.

Output array Answer[1..n]

Constraint: 1<=n,m<=100000, |a[i]|<=10^9, 1<=L<=R<=n, 1<=x<=n, 1<=y<=10^9.

Sample input

5
-2 -3 0 -5 -6
3
1 2 2 0
2 5 1 1
3 4 2 2

Sample output

1 2 0 3 -1

Note:

  • a[3] is non-negative already, Answer[3]=0.

  • After first query, a[] becomes {0,-1,0,-5,-6}, because a[1] becomes non-negative, Answer[1]=1.

  • After second query, a[] becomes {0,1,3,-1,-1}, Answer[2]=2.

  • After third query, a[] becomes {0,1,7,5,-1}, Answer[4]=3.

  • a[5] is still negative, Answer[5]=-1.

  • Vote: I like it
  • +17
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Are you sure? Subsequence? Isn't it substring/subsegment?

P.S. Can you provide a source of problem, please?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sub-sequence is contiguous elements, sub-sequence a[L..R] contains a[L], a[L+1], ..., a[R].

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      Subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. For example, the sequence  < A, B, D >  is a subsequence of  < A, B, C, D, E, F > . They should not be confused with substring which is a refinement of subsequence.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        Thanks, it's my mistake, i will update now.

        P/S: updated

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Technically, the way you wrote it wasn't incorrect: subsequence of the specific form A[L..R]. It was confusing, though.

          → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +13 Vote: I do not like it

Maybe, Persistent Interval Tree and Binary Search for every element ?

I mean, We can keep versions of interval tree after each query.

Then for every position do binary search and look up at defined version of persistent interval tree.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can Persistent IT support Lazy Update? I didn't try Persistent IT with Lazy update.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      We do not need lazy propagation, since nodes of the tree do not actually store any information about the segment (like minimum or sum), they just store x that we have to add when passing through the node, and y that we have to add for each element we skip after passing through the node.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Here is my implementation of this. Of course it's slower than the solution ValenKof suggested below and works for O(N * logN * logM), but it was still fun to implement this :P

    http://pastebin.com/HLhNJzeQ

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you, your code ran correctly from 0-th test to 20-th test, and got RE on 21-test (n = about 100000). I multiplied your array's size by 10 and your solution got AC. Your run-time on largest test is 1.99s.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, right, in build_st() instead of if (L == R) return new Vertex(a[L]); it should be if (L == R) return new Vertex(L < n ? a[L] : 0); so it doesn't try to access elements in A that do not exist. My bad.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Amazing, I have just learnt a valuable lesson. I used persistent segment tree and lazy update to solve this. Firstly, I estimate that the number of node is equal to n logn + m logn + 2n. But I have mistaken! There are only m queries but I asked n logm question to tree. So that number of node is up to n logm logn, too much memory!

      I will try to solve this without lazy update. And try the solution of ValenKof. It will work.

      → Reply
»
10 years ago, # |
  Vote: I like it +23 Vote: I do not like it

Transform every query q, such that a[i], l[q] <= i <= r[q], transforms to a[i] + x[q] + y[q] * i. Then create segment tree for x and y, initially empty. Then iteraty over a[i]. Some queries begin at i, some end. Update tree according to them. If a[i] >= 0 then ans[i] = 0. If a[i] + tree[0].x + tree[0].y * i < 0 then ans[i] = -1. Otherwise, you must find smallest prefix with sum(x) + sum(y) * i >= -a[i]. Segment tree can find it in O(logM). Total complexity O((N+M)logM).

P.S. code

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for your solution, I am reading it.

    Your solution got WA on this test case (and all of other tests)

    http://pastebin.com/fKBW4Nty

    There are no smaller tests.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      His code is correct, your problem statement isn't. According to this test case, values A[L]..A[R] are increased by x..x + (R - L) * y and not by x + y..x + (R - L + 1) * y.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I'm sorry about my mistake. I have updated my statement. I edited your code and your code got AC. Your solution solved the largest test in 0.90s. Thank you.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Try to add ios_base::sync_with_stdio(0) to begin of main. I think solution should be faster than 0.90s.

      → Reply
»
10 years ago, # |
  Vote: I like it -6 Vote: I do not like it

What is the time limit?

O(N log N sqrt(N)) approach is simple. Lets think about binary search for every number in array. Then each iteration check that number is non-negative or not. This can be done O(N^2 log N sqrt(N)). What about doing binary searches parallel. This observation leads us O(N log N sqrt(N)) solution. Between, sqrt(N) comes from this : Process last sqrt(N) query one by one and call this last sqrt(N) numbers onebyone list. If onebyone list's size is bigger then sqrt(N) update list with them and clear onebyone. One iteration is enough to increase all elements you can find out this yourself.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is a traning problem, there is no specified time limit. I expect to see a solution have complexity O(n polylog(n)).

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +6 Vote: I do not like it

Wrong idea. As is said: every problem has a simple, clear, obviously incorrect solution :D

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I thought it firstly. But it seems impossible. After applying an operator "add xi to A[i] for all A[L..R]" with node u, we can't maintain the value Max of node u.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It can be done using sqrt decomposition, see editorial to problem F from Zepto Code Rush link

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Sorry, but I misunderstood you. You say, that segment tree with operations "Find maximum from L to R" and "add x·i to Ai for all i from L to R" is classic and well-known? I know only one (UPD: now two, thanks to NuM) method of solving this problem, and it doesn't look easy.

    UPD: Here it is. Unfortunately, only russian version of description is available. I don't think, that it is possible to understand this with Google Translate or something similar, it is not completely full and not to easy to understand even in russian.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Whoops, it probably sounded that way. The "classic" part was due to persistent and such interval trees, mentioned in the comments above. I didn't really think about if it could be done... but I'll try to read the linked comment.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Really? I don't think that maintaining maximum with operations "add xi to A[i] for all A[L..R]" is easy and classical problem. Can you provide a link to implementation/descritption of the solution?

    → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I think that problem D in this contest is the origin of your problem: http://neerc.ifmo.ru/school/io/archive/20140322/problems-20140322-individual.pdf Your problem was given with a slightly modification in the input format. As I see in the archive, there are two solutions, one is , the other one is 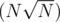. Both have a beautiful implementation.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How can you Google it???

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I solved this problem before. I remember that its name was jam, and it was from Russia. Finally, I found that pdf using Google :D

      → Reply