416A - Угадай число!
Используем стандартный подход к решению задачи А второго дивизион — в лоб. Будем поддерживать диапазон, в котором может находится искомое число. По мере считывания запросов в зависимости от ответов уточняем этот диапазон. Если в конце получился невырожденный диапазон, то берем любое число из него, иначе — "Impossible".
Посылка: 6606892
416B - Гильдия художников
В этой задаче достаточно пройтись по все художникам и работам в правильном порядке. Проходимся по всем художникам, запоминаем когда он закончил работу над каждым шедевром. Последующий художник начинает работу над данным шедевром не раньше, чем предудущий закончил.
Посылка: 6606994
416C - Система бронирования
Решаем задачу жадно. Необходимое наблюдение — в первую очередь нужно сажать группы, приносящие максимальную прибыль и сажать группу надо за подходящий столик минимального размера. Так что берем все группы в порядке уменьшения прибыли и ищем подходящий стол. Если подходящих столов несколько, то берем стол минимальной вместимости. Если подходящих столов нет, гоним данную группу на мороз. Ограничения в задаче позволяют искать столик для каждой группы полным перебором.
Посылка: 6617198
416D - Численность населения
Необходимое наблюдение в этой задаче — если мы покрываем какой-то отрезок одной арифметической прогрессией, то нам будет выгодно (ну или как минимум не хуже) взять как можно больше чисел в этот отрезок, т.е. расширить этот отрезок влево и вправо, насколько возможно. Соответственно жадное решение — берем самое левое число, не покрытое ни одной прогрессией, начинаем новую прогрессию в этой точке и пытаемся покрыть ею максимальное количество элементов. При этом надо внимательно рассмотреть все случаи, что можно а что нельзя покрывать одной прогрессией. В частности:
Если в отрезке нет ни одного фиксированного значения, то этот отрезок можно покрыть одной прогрессией.
Если в отрезке есть только одно зафиксированное число, то независимо от того, где оно находится, мы сможем покрыть отрезок арифметической прогрессией с шагом 0.
Если в отрезке есть два и более зафиксированных числа, то мы можем посчитать требуемый шаг прогрессии и все числа должны подходить под этот шаг. Шаг должен быть целым числом.
Если прогрессия возрастающая и есть некоторое количество незафиксированных элементов в начале, то надо проверить чтобы при заданном шаге этим незафиксированным элементам присваивались положительные значения.
Аналогично, если прогрессия убывающая, то брать незафиксированные элементы можно только пока значение, которое должно быть вставлено на эту позицию, положительно.
Посылка: 6607174
416E - Маршрут Президента
Будем рассматривать эту задачу на графе, данном в примере:
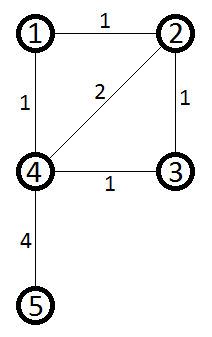
Нам надо посчитать сколько всего ребер лежит на всех кратчайших путях между какими-либо двумя вершинами. Рассмотрим сначала более простую версию задачи — посчитать только те ребра на кратчайших путях, которые входят непосредственно в конечную вершину (ту, до которой мы строили кратчайшие пути). Вот, например, ребра лежащие на кратчайших путях из вершины 4 в вершину 2, непосредственно ведущие в вершину 2:
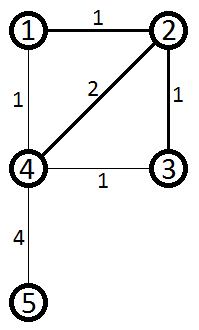
Введем для этого числа обозначение: inEdgessource, v — количество ребер, входящих в вершину v, которые лежат хоть на каком-то кратчайшем пути из source в v. В указанном примере inEdges4, 2 = 3. Введем также обозначение Ssource, dest — набор вершин, через которые проходит хоть один кратчайший путь из вершины source в вершину dest. Например, S4, 2 = {1, 2, 3, 4}. С этими двумя обозначениями нетрудно заметить, что количество ребер, лежащих хоть на одном кратчайшем пути из source в dest будет равно:

То есть ответом для вершин s и d будет сумма значений inEdgess, v для всех вершин v, которые лежат на каком-нибудь кратчайшем пути из s в d. Значит осталось посчитать эти самые S и inEdges. И то, и другое легко считаются, если известны кратчайшие расстояния между всеми парами вершин. Для вычисления этих расстояний используем алгоритм Floyd-Warshall. Полностью решение получается такое:
Считаем минимальное расстояние между всеми парами вершин алгоритмом Floyd-Warshall.
Считаем inEdges. Просто перебираем все вершины на роль источника, во внутреннем цикле перебираем ребра. Проверяем по минимальным расстояниям, будет ли это ребро находиться на кратчайшем пути от источника к какому-нибудь из своих концов.
Считаем ответ. Тройным вложенным циклом перебираем три вершины — source, destination и mid. Первые две — это вершины, ответ для которых мы ищем. Третья — это вершина, через которую должны проходить кратчайшие пути. Проверяем, что через mid проходит кратчайший путь из source в dest, если это так, то прибавляем к ответу inEdgessource, mid.
Все три шага имеют сложность O(n3).
Посылка: 6607257
Пожалуйста, не стесняйтесь репортить все опечатки, ошибки, неточности в личку.











please explain this test case for problem D
5 -1 -1 1 -1 -1
the accepted solutions prints 1 where the problem statements says "Values -1 may correspond to an arbitrary positive integer and the values ai > 0 must be equal to the corresponding elements of sought consecutive record of the progressions.".
can you tell me the expected progression for this case.
The progression in this case would be: 1 1 1 1 1. It is allowed to have a progression with step equal to 0.
416C — Booking System : how dp can be applied ? a hint ?
Something like the classical LCS -Longest Common subsequence- problem.
If the ith group can set on the jth table, then we try to seat them taking the benefit or to decide not to seat this group. else we pass the jth table going to the (j+1)th one.
Make sure to sort the two arrays of the input.
Hi, thanks for the hint,but I am not able to understand it completely, can you elabortate please,I am a beginner, Thanks! :)