И снова всем привет! Недавно, решая задачу 1937 с Timus'a (кстати, и вам советую! Отличная возможность отточить умения в строковых алгоритмах сразу в нескольких направлениях), я столкнулся с необходимостью нахождения всех подпалиндромов в строке. Опытные программисты уже знают, что одним из лучших алгоритмов для этого является алгоритм Манакера, позволяющий получить все подпалиндромы в сжатом виде без каких-либо дополнительных структур. Единственная проблема — алгоритм сравнительно сложен в реализации. То есть, его идея проста и понятна, а вот реализации обычно оказываются нагромождениями кода с повсеместным рассмотрением того, где написать +1, а где -1.
Для тех, кто не знает, или не помнит, опишу вкратце алгоритм Манакера. Сжатость по памяти в нём достигается за счёт того, что мы не храним индексы палиндромов, а для каждого элемента в строке храним половину длины наибольшего палиндрома, для которого он является центральным. Если речь идёт о палиндромах чётной длины, то центральным мы для удобства считаем элемент, который находится справа от центра. Скорее всего, с некоторыми изменениями таковым можно считать и тот, который находится слева.
Далее мы поддерживаем левый и правый окончания самого правого из известных палиндромов и, подобно тому, как это делается в Z-функции, мы сначала пытаемся инициализировать значение массива в этой точке, используя уже посчитанную информацию, а потом продолжаем действовать наивным алгоритмом. Если быть точным, мы можем проинициализировать значение p[i] значением в точке, симметричной относительно неё в имеющемся палиндроме, то есть, значением p[l + (r - i)]. Если речь о палиндромах чётной длины (вы уже тоже их ненавидите, да?), то нас будет интересовать значение в точке p[l + (r - i) + 1]. И да, стоит не забывать, что мы при инициализации не должны будем выйти за пределы известной нам части, то есть, инициализировать надо чем-то, что не больше, чем r - i (или r - i + 1 для палиндромов чётной длины).
Вот так нам предлагает строить алгоритм Манакера на e-maxx:
vector<int> d1 (n);
int l=0, r=-1;
for (int i=0; i<n; ++i) {
int k = (i>r ? 0 : min (d1[l+r-i], r-i)) + 1;
while (i+k < n && i-k >= 0 && s[i+k] == s[i-k]) ++k;
d1[i] = k--;
if (i+k > r)
l = i-k, r = i+k;
}
vector<int> d2 (n);
l=0, r=-1;
for (int i=0; i<n; ++i) {
int k = (i>r ? 0 : min (d2[l+r-i+1], r-i+1)) + 1;
while (i+k-1 < n && i-k >= 0 && s[i+k-1] == s[i-k]) ++k;
d2[i] = --k;
if (i+k-1 > r)
l = i-k, r = i+k-1;
}
Два отдельных похожих куска кода для палиндромов чётной и нечётной длины. И, если мне не изменяет память и это до сих пор не исправили, в них ещё и содержится ошибка (сможете её найти?)
Немного подумав и расписав некоторые случаи на листке бумаги, я смог сжать два отдельных куска в один, объединённый циклами. При этом, я постарался сохранить максимальную схожесть с алгоритмом построения Z-функции для мнемоничности.
vector<vector<int>> p(2,vector<int>(n,0));
for(int z=0,l=0,r=0;z<2;z++,l=0,r=0)
for(int i=0;i<n;i++)
{
if(i<r) p[z][i]=min(r-i+!z,p[z][l+r-i+!z]);
while(i-p[z][i]-1>=0 && i+p[z][i]+1-!z<n && s[i-p[z][i]-1]==s[i+p[z][i]+1-!z]) p[z][i]++;
if(i+p[z][i]-!z>r) l=i-p[z][i],r=i+p[z][i]-!z;
}
}
Однако, всю картину портит достаточно длинная строка с while. С этим я предлагаю бороться примерно таким образом:
vector<vector<int>> p(2,vector<int>(n,0));
for(int z=0,l=0,r=0;z<2;z++,l=0,r=0)
for(int i=0;i<n;i++)
{
if(i<r) p[z][i]=min(r-i+!z,p[z][l+r-i+!z]);
int L=i-p[z][i], R=i+p[z][i]-!z;
while(L-1>=0 && R+1<n && s[L-1]==s[R+1]) p[z][i]++,L--,R++;
if(R>r) l=L,r=R;
}
Как кажется лично мне, в таком виде код является наиболее читаемым и так в нём труднее всего допустить какую-то ошибку. А что думаете по этому поводу вы? Как реализовывать Манакера наименее мучительно? И вообще, как вы решаете задачу поиска всех подпалиндромов в строке? Поделитесь своими идеями в комментариях :)
UPD: droptable в комментариях рассказал о способе поддерживать массивы из алгоритма Манакера в онлайне. Здесь я выложил пример использования самого алгоритма с некоторыми изменениями, о которых будет сказано ниже.
Основная идея алгоритма: в любой момент мы поддерживаем центр максимального суффикс-палиндрома. Когда мы добавляем символ в конец, у нас есть два варианта того, что произойдёт дальше:
- Основной палиндром расширится. Тогда просто увеличиваем для него значение радиуса на единицу и на этом завершаем.
- Основной палиндром не расширится. Это значит, что нам нужно будет пройтись по массиву вперёд, чтобы найти новый основной палиндром. При этом каждый раз инициализируем новую ячейку в массиве числом в ячейке, симметричной относительно центра палиндрома, который был основным ранее. Как только оказалось, что мы можем расширить текущий палиндром, это означает, что он самый левый из касающихся конца строки, а значит, он станет новым основным. Завершаем на этом обновление.
Теперь об изменениях в коде. Во-первых, были убраны два символа-заглушки, которые вставлялись в строку вначале. Как оказалось, они не являются необходимыми, однако, их добавление усложняет алгоритм.
Во-вторых была добавлена функция get(). Михаил упоминал в своём комментарии некоторые проблемы с онлайном. Проблема была в том, что в любой момент мы знаем окончательные значения только в элементах, которые находятся ранее, чем центр основного палиндрома. Однако, можно заметить, что значения за ним мы можем получать за О(1), обратившись к симметричному относительно центра палиндрома элементу.











Ну просто охренеть как читаемо.
Есть вариант лучше?
Ну хеши + бинпоиск есть... Это ухудшает время работы, правда.
А ещё время написания и объём кода, не?
В любом случае, речь шла именно о Манакере. Да, эта строка не очень хорошая, но если понимать, для чего она, проблем возникать не должно...
при чём тут лучше? или у тебя другое видение "читаемости"?
При том, что эту статью я написал как раз для того, чтобы выяснить, в каком виде этот достаточно непростой в написании алгоритм проще для восприятия. Да, как я уже писал, строка, процитированная Алексеем не очень миловидна. Но лично у меня, например, сразу всплывает аналогия с Z-функцией, что упрощает её понимание. Способов вообще не писать подобного в Манакере не знаю, потому и поинтересовался.
Можно писать алгоритм только для строк нечетной длины, но при этом будет использовано немного больше памяти. Если у нас строка четной длины, например abba, то её можно преобразовать в строку a#b#b#a.
Интересная идея. Ещё и на выходе сразу даёт длину палиндрома, а не её половину, которую ещё надо распарсить
Расскажите кто-нибудь, где ошибка в манагере с e-maxx. Он нормально сдавался вроде в какой-то из здешних задач.
Так на емаксе в комментах написано же.
Ну, думаю, читаемость тут уже на вкус и цвет. Мне нравится вот эта реализация.
Мне Мне очень жаль
Why are you down voting him? He is describing an algorithm.
.
.
I think this may be helpful : http://leetcode.com/2011/11/longest-palindromic-substring-part-ii.html
I solved that problem in O(N*logN) using Hash. I think Hashing can replace Manacher entirely, can apply to more types of problem and is easier to implement :)
by hashing? how nlogn can u explain your process?
We choose position x and then find with bin_search the maximal palindrome with the middle in x!And we can compare two strings with the hashes in o(1)!
Can you please share your code? The problem which i am facing is while during binary search, even if the hash value is same on both the sides of the current x, it does not mean that the substrings will be the same, as there can be collisions. How do we handle this scenario?
Edit: However, i used double hashing to assume there will be no false positives, however this is still not accurate. Any leads would be definitely helpful.
If you feel insecure about a single hash just use two and you'll pretty much never run into any problems.
hey you sucker .... you published this before 2 days and APIO contest was running ... this algorithm is very useful for the first task
If i've read this during APIO I would've scored 100 points on the first task
and guess what it was published DURING THE CONTEST
Did the competitors have an Internet access during the APIO?
yes .... it's held online and the contest was runned for 2 days each delegation has an assigned time to do it
It's an unpleasant coincidence. I didn't know about APIO problems. Anyway, Manacher is pretty well-known algo and if you diligently searched for it, I guarantee that you would find something else even if my entry was not published. Also, you could made arrays from Manacher's algo with straightforward algorithm with hashing in O(nlogn). Anyway, my apologies, but I don't think that my entry seriously harmed APIO.
Actually I said that because you published them in the first day of APIO (manacher + suffix trees) and anyone of them is a key to solve the first problem ... BTW thanks for the blogs i believe they are too helpful i will read them soon
I published entry about suffix tree much earlier...
Here is the link to my implementation, it's a bit different to your code. Also it includes a function (quiet trivial) that is useful for checking if a given substring s[b...e] is palindrome.
.
В 35й строке undefined behavior, притом, как по мне, совершенно контринтуитивный.
Цикл while с простым условием не работает.
А не проще ли делать все не с начальной строкой, а строкой, между символов которой вставлен символ, допустим, #(тут даже не имеет значение, входит ли этот символ в начальный алфавит). Например, abacaba заменить на a#b#a#c#a#b#a. Тогда все палиндромы четной длины будут просто палиндромами, в центре которых #, в свою очередь нечетной — те, у которых в центре буква. То есть, центральный символ будет у всех. Таким образом, все палиндромы, найденные в новой строке, будут нечетной длины. Тогда не надо будет писать два разных алгоритма, проигрыша во времени тогда очевидно не будет(потому что не надо проверять строку на два различных типа палиндромов, четных и нечетных), по памяти в два раза. Но читаемость значительно повысится.
UPD увидел выше.
Can you please explain how you solved the Timus problem 1937 using Manacher's algorithm?
How common are Manachers' algo problems on Codeforces? Could someone give me links to some questions here on Codeforces.
Huh, readability is incredible in this article :)
Here is actual version:
Could you please explain what this code does in more detailed?
If this code is about Manacher's algorithm then I think it is wrong.
It calculates half-length of maximum odd palindrome with center in . For example, for
. For example, for 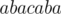 it returns
it returns  .
.
What is the use of characters "@" and "$"?
Using them we can get rid of cases when i - len or i + len are out of bound.
Can you please also put readable code for even palindromes?
In case of even palindromes I suggest to use the same code with the string s1#s2#... #sn
I made a mistake.
For input: "ArozaupalanalapuazorA"
Gives output: "1 1 1 1 1 1 1 1 2 1 11 1 2 1 1 1 1 1 1 1 1".
So, it works fine.
We can also solve this problem using Dynamic Programming using O(N^2) time and memory. We will store array dp[i][j] to memoize the function: f(i,j) = 1 if substring [i..j] is palindrome and 0 otherwise.
The base cases are all f(i,i) because a length 1 substring is always a palindrome, and also f(i,i+1) is a base case, because if s[i] = s[i+1] then f(i,i+1) = 1, otherwise f(i,i+1) = 0.
When i < j-1, f(i,j) = 1 iff f(i+1,j-1) = 1 and s[i] = s[j], otherwise f(i,j) = 0. So we can run f(i,j) for every pair (i,j) and in the end we will have a boolean matrix that will contain the indices (i,j) of every palindromic substring.
This algorithm should be optimal because we can have O(N^2) palindromic substrings (when every character is equal), so any algorithm that retrieves all of them should be at least O(N^2).
Here is my version:
It returns the array
L[i]— index of the beginning of the longest palindrome centered at positioni. (For both even and odd positions simultaneously.) If you need the end index, it is calculated by symmetry:R[i] = i - L[i]. And of course, the length of the palindrome islen[i] = R[i]-L[i]+1 = i - 2*L[i] + 1.I found much shorter implementation https://github.com/stjepang/snippets/blob/master/manacher.cpp
I like this implementation:
for(i = 0; i < n; i++){ if(i > r) k = 1; else k = min(d1[l + r — i], r — i);
while(0 <= i-k && i+k < n && s[i — k] == s[i + k]) k++; d1[i] = k; if(i + k — 1 > r) r = i + k — 1, l = i — k + 1; }
for(i = 0; i < n; i++){ if(i > r) k = 0; else k = min(d2[l + r — i + 1], r — i + 1);
while(i + k < n && i — k — 1 >= 0 && s[i+k] == s[i — k — 1]) k++; d2[i] = k;
if(i + k — 1 > r) l = i — k, r = i + k — 1; }
adamant Это очень полезный материал.
Только, можно уже исправить реализация, https://cp-algorithms.com/string/manacher.html ?
Многие не читают комментарий и сразу смотрят реализация в основном материале (включая я :).