I recently encountered an interesting performance issue while solving the "Sereja and Brackets". I implemented a Segment Tree-based solution but found that my code was giving a "Time Limit Exceeded" (TLE) on the 13th test case. After some investigation, I discovered that the issue was related to how I was initializing a vector.
Originally, I was adding 3 elements to the vector using push_back() in a loop. To improve the performance, I decided to initialize the vector with a fixed size of 3 upfront, like this: vector t(3, 0). Surprisingly, this simple change made a huge difference, and my code passed all test cases with ease.
After some searching, I discovered that one reason for the performance hit is that when we use push_back() to add elements to a vector, the vector may need to be resized. This resizing involves allocating a new block of memory, copying the existing data to the new block, and then deallocating the old block. This process can be time-consuming, especially if the vector is large or the constraints are tight.
To avoid unnecessary resizing and copying, it's often a good idea to reserve enough space in the vector upfront to accommodate all the elements we need to add. This can be done using the reserve() function. By reserving enough space, we can ensure that the vector doesn't need to be resized as often, and that the performance of our code become much better.
Overall, this experience taught me the importance of carefully considering how vectors are initialized in performance-critical code.
Soltuion 1 link which got TLE
Soltuion 2 link which got accepted
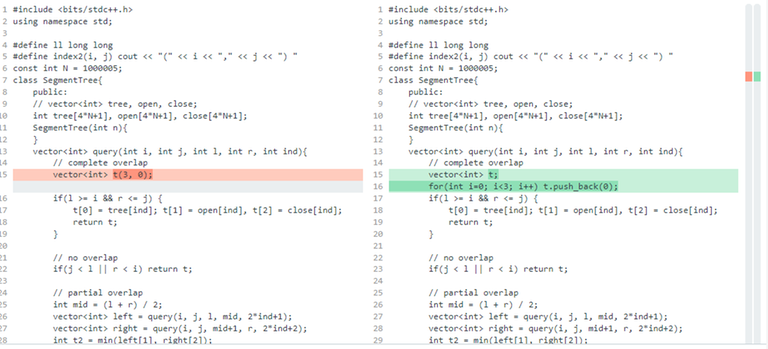











It seems that
std::array<int, 3>fits in your use case better..Yes, always use
arrayif the size is a constant you can calculate beforehand.It's still quite rare to run into time/memory limits with small vectors, unless you have a LOT of small vectors, but if it happens, it indicates a mistake in design. The bruteforce option is to flatten the
vectorand use a vector of indices for starting points of implicit "nested" vectors, but if you're not dealing with small variable lengths, just small constant length,arrayis the exact same thing as far as memory layout and therefore performance goes.Then there's the bad case when you don't know the sizes beforehand at all. What if the size of $$$(i+1)$$$-th nested vector depends on calculations with the $$$i$$$-th? Can't do much better than your approach, which is creating a vector dynamically. That makes sure no internal memory copying happens, but you still have to deal with cache misses especially if you don't access the vectors in some reasonably sequential-ish order (e.g. when pushing to $$$(i+1)$$$-th, you don't care about $$$(i-2)$$$-th or earlier), and you always need 2 memory accesses per vector — one in the outer vector for the nested vector and one for the required element in the nested vector.
For that matter, if you're processing a LOT of elements but in that sequential-ish order, consider deque with throwing away what you're not gonna need anymore, it saves memory.
There's a lot of possible options depending on what problem you're dealing with and it's just annoying implementation in what could otherwise be interesting problems, but you usually don't need to worry. Just switch to inner array if you can.
Another easy fix is to call
t.reserve(3)and thenpush_backthe elements, which will reserve the capacity upfront for you so it doesn't have to dynamically resize as it goes.