Given N distinct points on the plane. Find the pair of point with the smallest (and largest) Euclid distance between them.
I only know the Brute-Force O(n^2) algorithm to solve this.
Can someone give me any faster algorithm?
Thanks in advance.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Given N distinct points on the plane. Find the pair of point with the smallest (and largest) Euclid distance between them.
I only know the Brute-Force O(n^2) algorithm to solve this.
Can someone give me any faster algorithm?
Thanks in advance.
| Name |
|---|



There is a divide-and-conquer solution in O(n*log(n)), but this one is easier to implement,
I thought these are two completely different problems and you should not mix them. I believe the shortest distance could be found efficiently, but it is not so for the greatest one.
Convex hull + two pointers on it are O(NlogN) solution to farthest points problem.
I agree. I failed to note we are speaking of 2D space, sorry. But I was bewildered by the yellow color of the author's handle (since planar case is discussed in wikipedia). :)
I thought that closest pair algorithm could be generalized for any number of dimensions with the same asymptotic, but not the furthest pair. Though I may be wrong — am I?
Largest distance... well, it's between points on a convex hull. Out of points inside triangle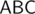 , the one most distant from point
, the one most distant from point 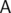 must be
must be 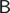 or
or  .
.
Also, the distance of vertices of a convex polygon from an arbitrary vertex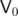 of this polygon would (as we travel along the perimeter) first keep increasing and then keep decreasing, so we can bin-search for the first pair of vertices
of this polygon would (as we travel along the perimeter) first keep increasing and then keep decreasing, so we can bin-search for the first pair of vertices 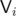 ,
, 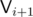 of which the first is farther than the second.
of which the first is farther than the second.
By repeating this for all possible choices of vertex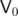 , we can find the most distant pair in
, we can find the most distant pair in 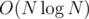 .
.
Edit: ninja'd :D
No need to bin-search. You can find the largest distance between two points on convex hull with rotating calipers method in O(k), where k is count of points in CH. There is good article here, but on russian. You can google-translate it or try to understand the main idea from pictures.
To everyone their own. I know the rotating calipers method (from CTU Open 2013, one problem was about finding a minimum perimeter bounding rectangle for a set of points), but I'd rather bin-search, because I could code it quickly and painlessly. And you still need to construct the convex hull in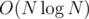 time.
time.
BTW you link is neither clickable nor readable. Maybe it's because of some special characters — anyway, it's better to not use the link as the shown text.
Of course bin-search is easier to implement, and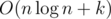 ==
==  , but if we know that points are on CH, we can compute it in linear time
, but if we know that points are on CH, we can compute it in linear time
Yes, I know. idk why old link didn't work, but now shortened link works fine
Are you sure that the distances from a fixed vertex of a convex polygon first increases and then decreases? Say that the polygon is very similar to an ellipsis, and the ellipsis is very thin. Take vertex roughly in the middle, then the distance first increases, then decreases, then increases, and then decreases again.
Not so sure now :D
I remember that some nice property should hold there, though.
I think for points that are part of a maximum distance pair it holds.
Why? You can have a situation similar to this: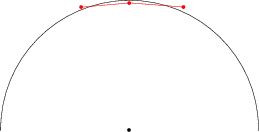
the maximum distance is between the bottom central point and one of the red points. But the red parts can be arbitrarily complicated: you can be within the circle, then outside, then within again, and so on...
"you can be within the circle, then outside, then within again, and so on" But then the polygon wouldn't be convex would it? That said, I can't prove that what I said is true, but the rotating calipers method makes a very similar assumption it seems (or maybe I'm wrong).
Why wouldn't it be convex? I can repeat the red part multiple times (after scaling down a little bit) and the resulting polygon will still be convex :)
I see. Clever, I guess this settles the argument :)
You can sort the point first by x-coordinate, then by y-coordinate. Call your current shortest distance D. When go through point P[i], get a set S consist of all point to the left of P[i] which Manhattan distance to P[i] smaller or equal than D. Run brute-force in S. One can prove that S has O(1) size. Good luck.
Smallest distance can be calculated in O(n*log(n)) for any dimension.
Largest distance also known as Diameter of a Set of Points.
site says unauthorized