correct me if i am wrong but can't this be solved using sieve? you can count number of multiples of k that is presented in your array where 1 < k <= 1e6 then whenever you find that you have number of multiple of k less than n and greater than or equal 1 all you need to is taking any number that is multiple of k with any number that isn't multiple of k time complexity O(klogk)

https://codeforces.me/contest/548/problem/E Here is a similar problem we can use inclusion and exclusion for this one and simple formula Nc2 we can solve this in o(n) * 2^7 7 is the max number of unique primes for any number lessthan 1e6 we can do it using bitmaks 01 bick the prime or leave it or we can use backtracking for the same idea Or we can solve it in o(n) * the number of divisors for each element search about that

what i think here is

we have to make a smallest prime factor for each no and store them now we create some hashset which contains the no of smallest prime factor divisor now we know that the no of pair of frequency of all the smallest individual prime no and we just calculate the all pair using some mathmetical calculations and the ans is [total pair] — [total pair which gcd >1] for example 2 4 6 8 3 9 so the point is

number-> smallest prime factor

2 -> 2

4 -> 2

6 -> 2

8 -> 2

3 -> 3

9 -> 3 so roughly we have 2's -> 4 time and 3-s -> 2 time

sorry i am bit lazy please complete this on your own :)

Please refer to this formula.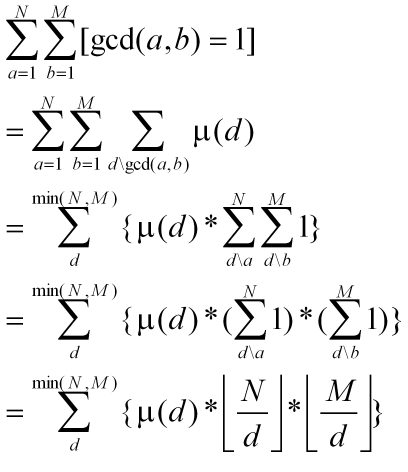

We just change the floor value of N/d to the multiple of d. We apply the sieve of Eratosthenes to find the number of multiple of d. My implementation is below. I hope it will help you.

#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int,int> P;
const static int maxn=1000002;
signed Eu[maxn];
bool vis[maxn];
int cnt[maxn];
signed prim[maxn];
signed minPrim[maxn];
signed top = 0;
void init_Prime()
{
	vis[0] = vis[1] = 1;
	for (int i = 2; i < maxn; i++)
	{
		if (!vis[i])prim[top++] = i;
		for (int j = 0; j < top&&i*prim[j] < maxn; j++)
		{
			vis[i*prim[j]] = 1;
			minPrim[i*prim[j]] = prim[j];
			if (i%prim[j] == 0)break;
		}
	}
}

signed mobs[maxn];
void mobius()
{
	signed cnt = 0;
	init_Prime();
	for (int i = 2; i < maxn; i++)
	{
		signed tmp_i = i;
		signed tmp_tmp_i;
		cnt = 0;
		signed miu = 1;
		while (vis[tmp_i] && tmp_i != 1)
		{
			tmp_tmp_i = tmp_i;
			cnt = 0;
			while (tmp_i%minPrim[tmp_tmp_i] == 0)
				tmp_i /= minPrim[tmp_tmp_i],cnt++;
			if (cnt == 1)miu *= -1;
			else if (cnt >= 2)miu *= 0;
		}
		if (tmp_i != 1)
		{
			miu *= -1;
		}
		mobs[i] = miu;
	}
	mobs[1] = 1;
	
}
int arr[maxn];

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	long long t, n, m, A, B,d, C, D,u,v,k,x,y,z;
	string str;
    mobius();
    cin>>t;
    //t=10;
    while(t--){
        cin>>n;
        for(int i=1;i<=n;i++)
            cin>>A,cnt[A]++;
//In this part, we use the sieve of Eratosthenes to find the number of d's multiple which is represented as cnt[d]
        for(int i=1;i<=1000000;i++){
            for(int j=2*i;j<=1000000;j+=i)
                cnt[i]+=cnt[j];
        }
        int ans = 0;
        for (int i = 1; i <= 1000000; i++)
            ans += mobs[i] * cnt[i]*cnt[i];//the floor of N/d and M/d is changed to the multiple of d
        cout << ans<< endl;
        
        memset(cnt,0,sizeof cnt);
    }
	return 0;
}

Check if any of them is 1, if found, then yes
Else, count the multiples of ai in the array, the count should be n if there is no j, such that gcd(ai, aj) = 1

Overall, you can solve this in AlogA, where A is 1e6

Hey! Do you have an opportunity to submit a solution for this task? If it's possible for everyone, could you share the link please?

I think that you can just sort your array in increasing order. After that you iterate over all i And you should check every j, such that i — 20 <= j < i. I think that is enough because the product of the smallest 20 primes is bigger than 1e6

Look up Möbius inversion

For each $$$x\le 10^6$$$, count how many multiples of $$$x$$$ there are in the array, and store this value in $$$\textrm{cnt}[x]$$$.

For each element $$$a_i = p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m}$$$ in the array, the number of elements in the array coprime to $$$a_i$$$ can be calculated by the inclusion-exclusion principle which gives the formula

Now for each array element we check if this value is non-zero, and if it is, we break and use another loop to find the corresponding element.

Iterate from 0..i until we get gcd(a0,a1,...,ai)=1, then can we say that there is an element at j from 0..i — 1 that gcd(aj,ai) == 1?

https://ideone.com/cOvEqC here is my solution, its complexity is O(n * 2^p) where p is at most 8. there is a corner case that can be handled easily which is when the gcd of all the array is greater than 1

Initial idea, might be wrong. Lets count gcd of our array from the start. At some index, lets call it $$$i$$$, it will turn to 1, that means that gcd of $$$a[i]$$$ and some element in $$$a[:i]$$$ equals one. Factorize $$$a[i]$$$ and for every its factor mark elements on our prefix that are divisible by it. In the end, we will have some unmarked indexes — take any of them.

find index for which prefix gcd equals to 1 and that will absolutely 1 of the number. then iterate over all the array and find another number which is coprime to the number at that index.

If we only want to find one such pair of ai, aj than we can divide it into two part :

base case if 1 is in the array just print it with any number

Part — 1 : Lets focus on finding one of the elements in the array a, such that the no. of elements that have gcd != 1 with it are < n — 1 , we can find it using the inclusion exclusion,

Part — 2 : we alreadty know one ai that gives me the solution than I can just iterate over entire array and find aj such that gcd(ai, aj) = 1