Hello, Codeforces!
The ICPC World Finals Dhaka will begin on November 10, 2022 at 11:00 (UTC+6). This is the culmination of the 2020-2021 ICPC season, and we have over 130 teams competing for the title of ICPC champion. Please join us on the live broadcast for the main event of the year in competitive programming; commentators will include ecnerwala, SecondThread, Egor, and more! There will also be a live mirror for you to solve the problems alongside the contestants!
Some useful links:
- ICPC Homepage
- World Finals Homepage
- World Finals Schedule
- Live Broadcast
- Live Scoreboard
- Contest Mirror/Judge!
All available broadcasts:
Good luck to all teams competing!










See you guys on stream!
Good luck, have fun to everyone competing, and good morning to everyone watching from home!
Sir, I had seen live cast of ICPC world final which was casting SecondThread & ecnerwala . I am a man in bangladesh. Bangladesh is host for arranging the icpc world final 2022 as first time. I am so proud for this reason. Thank you so much all the members of icpc officials. #icpcwfdhaka
I've just registered on judge.icpc.global. Is it correct that only one of a team needs to create an account, and then all teammates will use it to submit (we are not in the same place)? If so, then the "Full name (optional)" during registration kinda confuses
Is it rated?
It is the first time I found "is it rated" upvoted.
Codeforces Language Picker -- chrome extension to fix codeforces language picker.
Note: In 2022 Apple’s macOS, Monterey, has removed one of the longest and most prominent examples of using flags for languages (flags were used since 2001). Codeforces should do it too.
Are Petr, tourist and Endagorion going to participate unofficially this year?
Hope tourist will come !
I think the timeanddate link may not be set properly. It links to 11:00 UTC, not 11:00 UTC+6.
Fixed, thanks!
How can I participate the mirror . Why it said "There's no active contest for you (yet)." ?
Fixed now!
Good Luck to every participant TEAM (◠‿◠)
wow! good wf stream ,ovo
Is the mirror half hour later than offcial contest ?
When the problemset will be available?
Here is the problemset of ICPC WF 2021.
Why the mirror is delayed ?
Has the mirror started?
Mirrors are wave reflectors they can't start idiot
OMG, you are so crazy
It seems that the translation is dead.
Also looking forward to seeing the statements very much.
OMG, you are so crazy
it's called "stream"
https://www.merriam-webster.com/dictionary/translation the word "translation" has no meaning related to the streams
Thank you. I was too lazy to find the appropriate word.
I was completely bamboozled what you mean xD
How much is the mirror delayed?
who asked?
When will the mirror be ok?
It's always ok, but you need to register first.
Where can I get the problems?
https://judge.icpc.global/team/problems, remember to register and login.
Will there be mirror scoreboard?
This problem is same as problem H: https://atcoder.jp/contests/abc167/tasks/abc167_f?lang=en
Haha, I prepared it in 2017, and I'm sure there are earlier versions. Btw tests on Atcoder are weak.
Isn't that equivalent to L: swap space from ICPC World Finals 2016? Looks exactly the same modulo a different story
Yes, they are similar. A 'sort with correct comparator' problem. Also similar to this e-maxx article (in Russian). And I also prepared this and this which are similar too. A lot of clones exist.
a slightly harder version from PTZ-2009
Why do they live split screen while frozen time ? the result of submissions may be leaked on contestant's screen.
I think they intend to do so.
Results which I reversed engineered from split screen. Feel free to comment if there are any errors. Scoreboard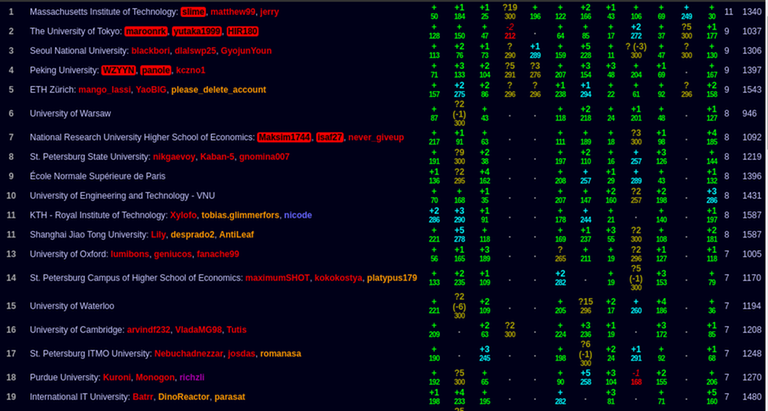
Good Luck For Everyone:)
why do i keep geting internal server error you fucking bitches
Who is owner of zibada.guru/finals? Is it zibada?
Could you help change 3rd member of "University of Engineering and Technology — VNU" on the website from SeehtEntity to Negativez2? This is the first Vietnamese team to (maybe, based on results shared here) ever win a medal, so I just hope their members are correct.
fixed :)
Thank you! And thanks for the great website!
Problem G already was in XXII Open All-Siberian Programming Contest (2021), which also was a GP of Siberia
Okay, it's a bit harder with up to 100 colors though, we don't have time to check each color separately.
here we need to create 100 different units and assign them to the colors instead of two, but I guess you know the solution anyway.
The point is, my prior knowledge of this problem reduced the time I needed to solve G to one (1) minute.
You only need log100 checks
Hi Tutis how able to check in log100? I try a random solution like for each color contains same bit i (0 <= i < 6) than mark as 1, else mark 0. Don't know why it was passed G.
You can solve for each colour bit independently and then AND the answers I think, idk what u are doing.
I tried to use bitsets with a size of $$$O(r_q c_q k)$$$ during the mirror. I knew I would fail
Managed to solve problem D during the mirror contest. That was too insane :)
wow, strong!
Apparently NQ passes in B. We wasted 2h writing $$$O(N^2 + Q \log N)$$$ ;_;
Our nq solution TLEed, and we were not able to speed up our code.
Yeah, TL seems stupid. A lot of teams report TL -> AC with $$$O(NQ)$$$
Yeah, we spent lots of time trying to end up with that time complexity and failed -- got so sad hearing that NQ passes.
We tried to time out $$$O(NQ)$$$, but unfortunately it looks like some optimized ones slipped by. Sorry! $$$O(N+QlogN)$$$ is possible, but we figured the problem was already extremely difficult; the graph was kept small so $$$O(N^2+QlogN)$$$ could pass.
Thanks for the answer. However, I'll just claim that I highly dislike the problems in which you have no idea whether your proposed complexity will pass or not (one might say that's a part of CP tho).
In case that you wanted to time out NQ and wanted to allow poly(N) + QlogN, can you kindly tell us what was the reasoning between not setting Q higher (1e6 order)? Thanks.
Note that I do not speak for the other judges, but yes, I also strongly prefer the challenge to be in finding the asymptotically correct solution, not optimizing constant factors on an easier algorithm.
All else being equal, there are good reasons to try to keep problem time limits low — feedback is faster and there's less pressure on the judge system (especially in the worst case where somebody submits an almost-correct solution 40 times). But, as it turned out, all else was not equal; in hindsight, I would have been in favour of a higher Q and higher time limit.
I looked at the constraints, thought "nq looks like it should pass", did not optimize anything and got AC with my first submit ¯\_(ツ)_/¯
If you wanted to time out nq at least make the constraints so that it looks like it shouldn't pass. I was convinced I wrote intended solution instead of thinking I cheated my way through with some optimized bruteforce
We had to implement LCA with RMQ to squeeze $$$O(N^2 \log N + NQ)$$$ to pass, another 50 lines worth of code.
And honestly I'm surprised that $$$O(NQ)$$$ is not intended, as NQ = 4e8, and the time constraint is 5 second. We have seen problems with more tight (time constraint)/(intended complexity) than 5s/4e8 operator
Have you thought about just precalculating all possible lcas in O(n^2) :p?
Somehow I completely forget that it's possible to compute LCA with arbitrary tree root in the same complexity as computing the LCA with tree rooted at fixed vertex (by doing some additional casework). Feel like a dumbass after the contest.
Hm, maybe we have a bit different solution then, but I did not need to move the root around. Actually the only reason I had lca as to compute a meeting point of 3 vertices and that is $$$lca[a][b] \oplus lca[b][c] \oplus lca[c][a]$$$ (with an arbitrary root)
Seems like the biggest predictor for success this contest was having Westin as your hotel, haha
how do we know the final ranking
why scoreboard still frozen?
here bro https://image.icpc.global/wfscoreboard/index.html
They updated it now, thx
How to solve K?
Wow, exciting extra Problem: onsite&reallife tech problem~!
Congratulations to heuristica!
And matthew99 and jerry, lol. Waiting for antontrygubO_o and TLE to beat this MIT result next year... oh wait
I bet jiangly next year :)D
In the stream someone mentioned that some teams used Python :) And used successfully. The system at ICPC has different time limits for different languages? And will it be possible to check the solution of the teams later?
The time limit is the same for all languages; there's no guarantee that a Python solution exists that can run in time. But Python was a good fit for problem C (which was very mathy), so there were a lot of Python submissions for that one.
For problem C, don't we just need to ensure that (q^n-(q-p)^n)/p divides m? Getting a WA verdict on the judge...
Edit: OK it seems that using t=(p^n-q^n)/(p-q) gives WA in python but using t=(p^n-q^n)//(p-q) gives AC... Why? (p^n-q^n) is divisible by (p-q) so it shouldn't have been a problem. I tried typecasting it to int too
Why are there pictures of the other 11 medal teams on stage, but not any of us on the official ICPC news page?
Did they not take any because I didn't immediately look at the camera? Or is it due to the masks? If so that's really sad :(
EDIT: they have a picture up now :)
Will there be an editorial released for the problemset?
Here are brief solutions to the problems I know:
Let's say that $$$f(x, y) = 1$$$ if there is a molecule there, otherwise $$$0$$$. Each wind direction $$$w$$$ essentially tells us that in some points $$$f(x, y) = 1$$$, $$$f(x - w_x, y - w_y) = 0$$$, and for all other pair of points that differ by vector $$$w$$$ we know that $$$f(x - w_x, y - w_y)\geq f(x, y)$$$. Therefore, in the end we have a graph (it may have $$$10^7$$$ edges, but we can store it in a compressed way). If for each valid inequality we add an edge $$$(x, y)\to(x + w_x, y + w_y)$$$, then we can propagate all guaranteed ones through the reverse edges and all guaranteed zeroes through the forward ones. Every unspecified cell in the end can be replaced by either zero or one.
Let's root the graph by the vertex $$$s$$$. Then almost every edge must be passed through at least two times. More specifically, if we end in the vertex $$$f$$$, then all edges of the simple path between $$$s$$$ and $$$f$$$ must be traversed an odd number of times (some of them 1, some of them 3, depending on the lca and stuff), and all other edges must be traversed an even number of times (turns out, they can all be traversed exactly 2 times).
We can group all queries by $$$s_i$$$ and handle all of the queries with fixed $$$s_i$$$ one after another, so that we don't need to reroot the tree. We can probably do something smart in $$$O(q\log{n} + n^2)$$$, but our team didn't need to.
I have a feeling that this problem has a lot in common with this last year problem.
After every round, the profits are proportional to $$$(1, 1 - f, (1 - f)^2, \ldots, (1 - f)^{n-1})$$$, therefore, in the end they must be proportional to the same. If $$$1-f = p/q$$$, then we need to find such $$$p$$$ and $$$q$$$ that the value of $$$p^{n-1} + p^{n-2}q + \ldots + q^{n-1}$$$ divides $$$m$$$.
Since $$$n\geq 6$$$, we don't need to try a lot of values, and all values can be computed in a naive way, without fancy geometric progression formulas.
As my teammate said, "generate all points, all rays through vertices, all perpendiculars, run something on them, the problem is finished".
He was not very happy.
For each color $$$i$$$, create a unique complex number $$$w_i$$$ with $$$|w_i| = 1$$$. For the motif we create a polynomial from $$$\mathbb{C}[x, y]$$$ where "color" $$$0$$$ corresponds to the coefficient $$$0$$$, and color $$$i$$$ corresponds to coefficient $$$w_i$$$. For the mosaic we create a similar polynomial, but all the coefficients are reversed (so that $$$(i, j)$$$ corresponds to the coefficient of $$$x^{n-1-i}y^{m-1-j}$$$), and color $$$i$$$ corresponds to $$$w_i^{-1}$$$. Then when we multiply these polynomials (2d fft), we are interested in the coefficients equal to the number of nonzero colors in the motif (all other coefficients have absolute value strictly less).
Sort all strings with nonnegative total balance in the decreasing order of minbalance. Then rotate all other strings by $$$180^{\circ}$$$, and do the same with them and concatenate them from the end. Why this works? Exercise for the reader.
Add bridges from the farthest from the center to the closest. Initially, the answers are like $$$\ldots, 3, 2, 1, 0, 1, 2, 3, \ldots$$$. Every time we add a bridge between $$$i$$$ and $$$i + 1$$$, let's say the answers for them were respectively $$$x$$$ and $$$y$$$. Then now the answers at most $$$y$$$ and $$$x$$$, and some of them are even less: while any two adjacent values differ by $$$2$$$, decrease the maximum of them by $$$1$$$. It is straightforward why these operations take sense. It is still not very difficult to prove that these operations are sufficient.
So now the solution is: find $$$x$$$ and $$$y$$$. If they are equal, do nothing. Otherwise, let $$$y = x + 1$$$. If the new value before $$$y$$$ (which was before $$$x$$$ earlier) is $$$y - 2$$$, decrease $$$y$$$ by $$$1$$$. Then look at the maximal chain of type $$$(x + 2, x + 3, \ldots)$$$ after $$$x$$$ (earlier after $$$y$$$) and reduce it all by $$$1$$$. This can be done via segment tree.
Calculate for every node the set of all points that can result in this node.
Claim. For a set $$$S$$$, we don't need to consider any point inside the convex hull of $$$S$$$.
After this we just calculate some Minkowski sums and then take convex hulls of their unions. The total size of all the convex hulls on each layer is about the size for the previous layer plus the size of the previous layer. Indeed, if $$$D$$$ is the set of all directions of sides of the children polygons $$$P_1$$$, \ldots, $$$P_k$$$, then the directions of any sum $$$\pm P_1 \pm P_2 \pm \ldots$$$ is also $$$D$$$. Then, when we take the convex hull of the union, probably we add at most $$$k$$$ new directions, idk.
Run the naive iteration in $$$O(n^2m^2)$$$. If you don't allocate vectors every time and reuse the same memory, it will work fast enough.
Author's solution also uses the fact that there only $$$k\leq 100$$$ markers, so each sequence of markers-non-markers can be encoded with a sequence of $$$k$$$ indices of markers.
UPD: It will not pass time limit
Alternative solution for problem $$$G$$$ with $$$z-function$$$ $$$(z-algorithm)$$$.
Let's mosaic has $$$n$$$ rows and $$$m$$$ columns, and motif $$$n1$$$ rows, $$$m1$$$ columns. Let's make one-dimension array $$$a$$$ of size $$$n*m$$$ from mosaic concatenating it's rows and $$$c$$$ one-dimension array of size $$$n1*m$$$ from motif concatenating it's rows extended with $$$m-m1$$$ $$$0$$$. Now we need to find where $$$c$$$ is a substring of $$$a$$$ assuming $$$0$$$ can be any symbol — we can do it using slightly modified z-function.
the only change will be in $$$while$$$ condition.
s[z[i]] == s[i + z[i]]tos[z[i]] == 0 || s[z[i]] == s[i + z[i]]the full while (you can compare it to e-maxx code, which i took to modify):
while (i + z[i] < n && (s[z[i]] == 0 || s[z[i]] == s[i + z[i]])) ++z[i];I have made some tests and it works. Correct me please, if it is wrong.
It will work correct, but complexity will be $$$O((n \times m)^2)$$$
It is very interesting solution, bro)
For problem D, the guard first moves between the starting point and the vertices of the polygon and then heads to a location where half of the target can be seen.
In the first part, it needs to check whether the segment connecting two points is fully inside the polygon (Airport Construction helps), and find the shortest path from the starting point to each of the vertices.
In the second part, if the starting point or the vertices of the polygon can see the target, no more moves are needed from that point. Otherwise, it needs to straightly move to the closest point on the boundary of the target region, which consists of $$$O(n)$$$ segments. Some of the segments are on the boundary of the polygon and it is no need to consider such segments, and each of the others is on the ray from the target heading to a vertex of the polygon, which may be considered as connecting the target and the farthest intersection between each edge and the ray that can see the target. Checking whether a point can see the target is straightforward based on checking the segment inside the polygon. Don't forget to check whether the "straightly move" is fully inside the polygon.
The total complexity is $$$O(n^3)$$$, $$$O(n^3\log{n})$$$, or even $$$O(n^4)$$$, based on the complexity of checking whether each of the $$$O(n^2)$$$ segments is fully inside the polygon. The precision issue is just metaphysical. I have used long double for calculation, tried several values of $$$\epsilon$$$ (precision tolerance), and somehow made it pass.
I think the visibility part is actually quite a bit easier than airport construction because it only asks for left or right visible (which means some of the weird edge cases there never occur). One can also prove that it suffices to check left/right visible for movement as well, so the whole "line segment in polygon" part is pretty straightforward
For problem K, based on the strange(?) constraints, it turns out that the conclusion that the maximum size of the convex hull in $$$[-D, D]$$$ is $$$O(D^{2/3})$$$ helps in my analysis.
For each non-leaf tree node $$$u$$$, denoting the number of children of $$$u$$$ by $$$a_u$$$ and the number of leaves in the subtree of $$$u$$$ by $$$b_u$$$, we have $$$1 \le a_u \le 100$$$ and $$$\sum a_u \le n$$$, and $$$\sum b_u \le 10 \cdot n$$$ since the height of the tree is no more than $$$10$$$.
The range of coordinates in the convex hull of $$$u$$$ is $$$[-1\,000 \cdot b_u, 1\,000 \cdot b_u]$$$, then the "cost" of calculating some Minkowski sums and then take convex hulls of their unions for a non-leaf tree node $$$u$$$ is about $$$a_u \log_2{a_u} (1\,000 \cdot b_u)^{2/3}$$$.
A rough estimate of the maximum total "cost" is about $$$6.644 \times 10^8$$$ when $$$n=10\,000$$$ and $$$100$$$ of $$$a_u$$$ reach $$$100$$$ and the corresponding $$$b_u$$$ reach $$$1\,000$$$. Since the variables about the structure of the tree and the size of the convex hull on each tree node can hardly reach the maximum generally, I think even the order is overestimated.
I wonder if it is possible to analyze the total "cost" in a more precise way or without the range of the coordinates.
I wrote K (which is a bit of a mess, I know), and I agree that analyzing the actual worst-case "cost" seems to be very hard. My original solution actually involved one angle sweep for the entire tree (rather than for individual Minkowski sums). The best I could prove was some limit with a 4^(tree height) factor, but in practice the number of updates was nowhere close. Trying to bound the solution based on the integer lattice isn't great either, since the real convex hulls don't come anywhere close to maximal (cough vanity link cough). I think the bounds we chose made it possible to convince yourself that the worst case wasn't going to get TLE, but in practice it probably required a bit of a leap of faith.
I don't think anyone's mentioned the "simple" solution yet that Errichto covers in the official solution video. Since you can greedily find minimal/maximal solutions along any given projection line, you can recursively trace the convex hull of all possible final solutions. I think none of the teams found this solution, and we also didn't discover it until late in the process (when we were discussing how to defeat heuristic loop-over-the-angle solutions, and then realized that this was one heuristic solution that was actually correct). Amusingly, the O(convex hull size * tree size) runtime of this solution does NOT depend on the degree or height limits in the problem. It's a little slower than the Minkowski-sum approach, but still runs fast enough (and further hard-to-analyze optimizations based on bounding distances are also possible).
We thought there was a possibility somebody might stumble on the "simple" solution early and then, as sometimes happens, there would be a follow-the-leader effect and a bunch of teams would find it.
Second solution is very cool, super easy to implement. I believe it is made easier if we add to the convex hull only the vertex in the direction pointing outwards (ignoring the one in the opposite direction even if it is not within the current convex hull). Not sure if that was emphasized.
For the first solution I believe that Kamil described that in such a naive way that its actual complexity is $$$O(NHK^2 \cdot \log)$$$ instead of $$$O(NHK \cdot \log)$$$ as claimed, but it can be easily improved to even $$$O(NH \log K \cdot \log)$$$ (basically deeming the degree constraint useless)
You're right, I don't think that was spelled out. The greedy algorithm naturally spits out maxima/minima, but you really just need the maxima that points outside the current convex hull (as long as you initially recurse on, say, [L,R] and [R,L] to get both sides of the hull). So you're just divide-and-conquering, you don't need to maintain the hull as you go.
Thanks for your great work! The "simple" solution looks pretty good, and I will check the official solution video for more information.
Some of my friends tried Minkowski sums during the mirror contest without complexity analysis or they just somehow belived that works fast. So I think it is acutually a hard but interesting work to analyze the complexity in many strict ways :)
$$$O(N*Q)$$$ solution works.
First, run topo sort to find the length of each sequence.
Then for each query, move up its parent(s) until one reaches 1st sequence.
Given that our answer is $$$k^{th}$$$ index of $$$x^{th}$$$ sequence, based on how it was created and the type of operation split/merge, we can find to which input sequence and index it belongs.
Keep repeating it until one reaches sequence 1. We know that sequence 1 is the identity sequence.
For problem H, what does "rotate all other strings by 180 degrees" mean exactly?
Reverse and then replace
(by)and vice versawe did naive iteration (with vectors) for L. Now that I think about this, you could precompute the time needed to move $$$(dx, dy)$$$. This gives a simple $$$O(nmklogk)$$$ solution if you use sorting and $$$O(nmk)$$$ if you use bucketing.
Does have any discussion regarding to solution for problem E?
(one small rant, sorry) [1.20hr debugging time, 3WA]
Am I the only one who assumed that 1, 2, ..., n is the topological order in problem J? Like it's written that the numbers form a consecutive sequence (yeah, I understand that it means that it's a permutation of 1 to N but come on). [from the statement: The overall input is identified by 1, and the remaining input/output identifiers form a consecutive sequence beginning at 2]
Of course, it is topological in all 3 samples. So annoying.
The overall input is identified by 1, and the remaining input/output identifiers form a consecutive sequence beginning at 2.Idk why, but I assumed that this means 1,2,..., n is topological order.
We have 8 WAs on the scoreboard. My teammate coded it along with topological ordering. During debugging, the first thing I did was remove this part. After fixing other bugs, once we were certain that the code could not have any other bugs. We submitted with assert, only to find this isn't true. Then we rewrote this part, only to get an AC at 3:30 hrs.
Yeah, I literally read my code 10 times and was so convinced that there can be nothing wrong. Even when my teammates, after a long debugging, told me that might be the problems, I first refused to believe as I don't know, they are consecutive. Of course, any stress tests that I have written aligned with my understanding of the task.
[My opinion only, as this is my first and last WF]: It's such a shame that literally places 8-30 or similar are majorly influenced by how much time you spent debugging J regarding this awfully written piece of description + deciding whether to go or not with O(QN) in B. A competition this prestigious should not be decided on this vague and semi-random behaviour -- why don't you just put that in the samples? Insane.
As I definitely agree that it is rather an ass move from organizers, you could have dealt with this issue better too from a strategical point of view I think. This is a 5 mins coding problem that many teams did not have problems with. If you are losing your mind over debugging it, it likely means you fell in some trap that will be hard to realize for you. In such case it is the best to just let your teammate code it from the scratch, because he will likely not fall in the same trap (it is important to NOT let him know anything about this problem)
Yes, I fully agree that we should have handled it better. However, regarding the
it is important to NOT let him know anything about this problem, what my first thought after getting a WA on a problem that I'm convinced it should pass is to ask my teammates to sanity-check my idea and take a look at my code for some silly mistakes.I guess, given the difficulty of the problem, that probably the best way to deal with it is to ask to reimplement from zero. Thanks for the advice.
"what my first thought after getting a WA on a problem that I'm convinced it should pass is to ask my teammates to sanity-check my idea and take a look at my code for some silly mistakes." — that makes some sense as well. However you have 2 teammates, so if you want to ask sb for sanity-checking you can use help of one and leave second one "uninfected" :D
Love the redemption story of matthew99!
From whining to winning
It's nice to see other names of universities at the top of the scoreboard! (I'm talking about EU universities)
I think that D is super similar to luggage problem from WF 2007. Back then Warsaw team solved it and won finals by doing so. You would think that the level of competitors increases, so someone should be able to solve D today! But yeah, it is not fun, just pain (and that is said by a fan of geo)
Totally agree (we didn't have time for D tho)
Participated in the mirror with e3c8f1a924 and yyandy, with 6 problems passed and 872 mins of penalties. F is not so hard as it is on the scoreboard for me, and I'm not smart enough to come up with the FFT idea of G. One of my teammates struck in the edge case of B, and sadly didn't solve until the mirror ends.
By the way the same question with Radewoosh: will there be a mirror scoreboard?
Hi there! Please, leave your feedback about the live broadcast here. Thanks for watching!
MIT team rocks.
Congratulations Champion MIT
B站加1分
Also, the typo in G was quite badly handled. It is a very important thing to note for contestants and the only way it was communicated was through an announcement in the system which was present from the very beginning. It was quite easy to miss it as at the beginning you frantically read all the problems etc., you may not even note it is there and later on you can simply forget about it even if you've seen it was there. I know that this affected me when writing mirror (as I was possibly considering bitsets solution which would be out of the question for raised limits) and I know it affected Warsaw team even more (apparently our top participant wasted 40 minutes because of this). It should have been both 1) said quite loudly before the start of the contest that there is a typo in constraints in one of the problems, 2) corrected using pen on already printed statements. System announcement is just far too easy to miss for such a crucial mistake by organizers.
My team was also ruined with 75 minutes and 5 penalties due to this typo in G.
It's my lack of attention, but as you said, I wish it was more easily noticed(like the announcement during the codeforces contest).
We also didn't see the announcement but due to bad reasoning I somehow hardcoded $$$i+j*1010$$$ which made our solution work. (Idk if it's correct still)
We even did not see the announcement during the contest. My first submission used long double and got Time Limit Exceeded. Then I simply changed to double and passed. I was also wondering at that time how could long double not pass the time limit with arrays of length $$$2.5 \times 10^5$$$ and only knew that there was an announcement about this after the contest.
A fun fact: In SWERC 2020-2021, the statement of problem G (yeah, again problem G) had a wrong range of input data. They wrote something like $$$10^5$$$ but the test cases contained something like $$$10^6$$$. We opened that problem very early and kept getting Runtime Error and the whole contest for us was ruined. Before this World Finals, I changed all codes in my contest library to using vector instead of global static array and thus luckily avoided the issue this time.
Hi! The judge isn't working. Someone know another judge with the WF Dhaka problems?
Bumping this with hope.
Bumping this with hope.
Hi, I just saw this and made some inquiries. Kattis didn't run the WF this year, but I think they have the data and hopefully they'll mirror it soon. Also, the judge data should be posted on the ICPC page within a few days. Sorry for the vagueness; it was an unusual year. I'll make sure the data ends up somewhere.
EDIT: The judge data is up on the ICPC site. It's not as good as a mirror, but it's better than nothing.
Thx!
I have uploaded all the tasks and official standings to QOJ. You can upsolve the problems or start virtual contest here.
Please note that since the official contest archive does not contain any checkers, I have implemented the unofficial ones. Please contact me if there are any bugs in the checker.
_
hihihiha
I've added the contest to Codeforces. You can find it here.
Happy coding :)
After all this time, I'm shocked to find out that problem H is not original. The EXACT same problem can be found in here. The official solution for problem H can be submitted there with minimum changes in the way output is formatted, and it gives AC.
Also, to make things worse, my code that gave AC in the world finals, is giving WA in the original problem. So, not only the problem is not original, but it also has weak testcases. Wow.