Начнём с конца.
Задача С. Commentator problem
Пусть R это расстояние из точки А до какой-то окружности с центром в О и радиусом r. Тогда из точки окружность видна под углом 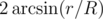 .
.
Таким образом три стадиона видны под одним углом если R1 / r1 = R2 / r2 = R3 / r3.
Возьмём две различные точки A, B. Множество точек C таких что AC / BC = const является либо прямой - серединным перпендикуляром AB, либо окружностью с центром где-то на прямой AB, которую легко вычислить по двум точкам лежащим на прямой AB для которых выполняется условие на AC / BC.
Положим X1 это множество точек из которых под одним углом видны стадионы 1 и 2, а X2 определим аналогично только для стадионов 2 и 3. Понятно что ответ принадлежит пересечению X1 и X2. Поскольку центры всех трёх стадионов не лежат на одной прямой то кол-во точек в пересечение X1 и X2 будет конечным.
Проверим их все: искомая точка должна быть ближайшей к какому-либо из стадионов. Так как стадионы не пересекаются, то такая точка не будет лежать внутри стадиона.
Как получить большую окружность для множества X1: поместим центры стадионов в точки находящиеся далеко, например (0, 0) и (1000, 0). Отношение радиусов стадионов должно быть как можно близким к 1, например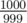 . центр и радиус новой окружности будут иметь порядок 106 Ответ надо знать с точностью до 10 - 5. Грубо говоря, нужно 11 знаков, типа double точно хватит.
. центр и радиус новой окружности будут иметь порядок 106 Ответ надо знать с точностью до 10 - 5. Грубо говоря, нужно 11 знаков, типа double точно хватит.
Очень интересно узнать на чём валились решения этой задачи.
Пусть в конце мы получили положительное число N = 2k· 5m·(другие простые). Количество нулей на конце N равно min(k, m). С помощью динамики найдём наименьшее возможное значение k (пусть это k1 ) и наименьшее значениe m (соответственно m1), а также пути приводящие к этим значениям. если k1 < m1 то выберем путь соответствующий k1, иначе m1.
Таким образом, min(k, m) это верхняя оценка ответа. Докажем что это и нижняя оценка. Пусть существует путь приводящий к числу с количеством нулей меньшим чем min(k, m). Тогда в разложении получившегося числа либо показатель степени при двойке k < k1 либо показатель степени при пятёрке k < k2. Получили противоречие.
Значит, достаточно получить показатели степеней 2-ек и 5-ок в каждом числе и прогнать на двух получившихся матрицах динамику.
В случае если в матрице присутствуют нули, надо отдельно посчитать пути проходящие через них и не проходящие.
Заменим все 0 на 10 и используем метод описанный выше, при этом для путей проходящих через нули мы будем получать результат с как минимум одним ноликом на конце. Если метод вернул путь с результатом без ноликов на конце, то он является ответом. Иначе можно взять любой путь проходящий через нолик.
Итого сложность алгоритма зависит только от сложности динамики, то есть это O(N· M).
За первый проход считаем сумму очков каждого игрока в конце игры. Пусть M - максимум среди сумм. Далее заново проходим по конам. Если в каком-то кону очки игрока X стали не меньше M и в конце игры X будет иметь M очков то выводим ответ и выходим из программы.
Следующий тест иллюстрирует тот факт что игрок может набрать больше M очков, затем слить часть очков а в конце победить.
Input:
Masha 12
Masha -5
Sasha 10
Masha +3
Output:
Masha
Задача С. Commentator problem
Пусть R это расстояние из точки А до какой-то окружности с центром в О и радиусом r. Тогда из точки окружность видна под углом 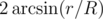 .
.Таким образом три стадиона видны под одним углом если R1 / r1 = R2 / r2 = R3 / r3.
Возьмём две различные точки A, B. Множество точек C таких что AC / BC = const является либо прямой - серединным перпендикуляром AB, либо окружностью с центром где-то на прямой AB, которую легко вычислить по двум точкам лежащим на прямой AB для которых выполняется условие на AC / BC.
Положим X1 это множество точек из которых под одним углом видны стадионы 1 и 2, а X2 определим аналогично только для стадионов 2 и 3. Понятно что ответ принадлежит пересечению X1 и X2. Поскольку центры всех трёх стадионов не лежат на одной прямой то кол-во точек в пересечение X1 и X2 будет конечным.
Проверим их все: искомая точка должна быть ближайшей к какому-либо из стадионов. Так как стадионы не пересекаются, то такая точка не будет лежать внутри стадиона.
Как получить большую окружность для множества X1: поместим центры стадионов в точки находящиеся далеко, например (0, 0) и (1000, 0). Отношение радиусов стадионов должно быть как можно близким к 1, например
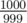 . центр и радиус новой окружности будут иметь порядок 106 Ответ надо знать с точностью до 10 - 5. Грубо говоря, нужно 11 знаков, типа double точно хватит.
. центр и радиус новой окружности будут иметь порядок 106 Ответ надо знать с точностью до 10 - 5. Грубо говоря, нужно 11 знаков, типа double точно хватит.Очень интересно узнать на чём валились решения этой задачи.
Задача B. Наименее круглый путь
Решим задачу для случаев где матрица вся положительная.Пусть в конце мы получили положительное число N = 2k· 5m·(другие простые). Количество нулей на конце N равно min(k, m). С помощью динамики найдём наименьшее возможное значение k (пусть это k1 ) и наименьшее значениe m (соответственно m1), а также пути приводящие к этим значениям. если k1 < m1 то выберем путь соответствующий k1, иначе m1.
Таким образом, min(k, m) это верхняя оценка ответа. Докажем что это и нижняя оценка. Пусть существует путь приводящий к числу с количеством нулей меньшим чем min(k, m). Тогда в разложении получившегося числа либо показатель степени при двойке k < k1 либо показатель степени при пятёрке k < k2. Получили противоречие.
Значит, достаточно получить показатели степеней 2-ек и 5-ок в каждом числе и прогнать на двух получившихся матрицах динамику.
В случае если в матрице присутствуют нули, надо отдельно посчитать пути проходящие через них и не проходящие.
Заменим все 0 на 10 и используем метод описанный выше, при этом для путей проходящих через нули мы будем получать результат с как минимум одним ноликом на конце. Если метод вернул путь с результатом без ноликов на конце, то он является ответом. Иначе можно взять любой путь проходящий через нолик.
Итого сложность алгоритма зависит только от сложности динамики, то есть это O(N· M).
Задача А. Победитель
Простая задача на реализацию.За первый проход считаем сумму очков каждого игрока в конце игры. Пусть M - максимум среди сумм. Далее заново проходим по конам. Если в каком-то кону очки игрока X стали не меньше M и в конце игры X будет иметь M очков то выводим ответ и выходим из программы.
Следующий тест иллюстрирует тот факт что игрок может набрать больше M очков, затем слить часть очков а в конце победить.
Input:
Masha 12
Masha -5
Sasha 10
Masha +3
Output:
Masha











task B, submission #3726143, I got:
Can I see what concrete input was in this test to find the reason? And who is Yuri? ))
There is one zero in the test — the best answer.
you saved hours of debugging. Thanks mate
could someone help me with the problem B, please ?
here's my code: http://ideone.com/1Juljl
thanks in advance :)
why didn't it appear in the recent actions? I need some help.
why problem B is O(n*m)? isn't it o(n*n)?
what is wrong with this solution http://codeforces.me/contest/2/submission/44454112
It fails in test 10.
Take a simple test:
Answer: b
[Solved]
In problem B if the input is
3
1 2 3
4 5 6
7 8 9
can one solution could be RRDD too?
Yes, I think so. Usually in the problem statement, it says "if there are more than one such path, print any possible path." I don't know why they didn't say it in this problem.
Problem A)
Failing test case 10 W.A Can anybody please help me ?
my submission link is here — https://codeforces.me/contest/2/submission/94976880