In C1, $$$dp[i]$$$ can be simply interpreted as the number of good sub-arrays that end at index i. The code is precisely the same.

Please update the contest announcement page and the contest page to reflect the editorial, some people could not find this and are waiting for it!

Why do editorialists still do this? Making it a challenge to read problem solutions without spoiling solutions of other problems that one hasn't solved. Do they not know of the existence of the spoiler option?

As I read the editorial for problem C, I now have an extra challenge to avoid any sneak peak/peripheral vision from wandering by chance/accident to solution for B and C2, both of which lie directly above and below resp. to the solution to the problem I'm reading.

It's pathetic. I wish editorialists weren't this lazy.

Is there any better explanation for problem B?

C1 binary search approach:

Suppose we have a range [L,R] which isn't a good subarray.

For this range, the worst element is the element a[j] for which a[j]-j is too low (minimum on the range [L,R]).

So we can have another array b for which b[i]=a[i]-i, then we build a Sparse Table over array b. Now we can iterate over all indices of array a, and binary search the farthest length of good subarray [i,R] for all 1<=i<=n.

And because, whatever the minimum b[j] on range [i,R] is going to be, it still shares the same prefix i-1 with all the elements on the range [i,R], then we can check if query(i,R)+i-1 is bigger than or equal to zero, or not, to edit our searched range.

The binary search is going to be like this:

for(int i=1 ; i<=n ; i++)
{int L=i,R=n,h=i;
while(R >= L)
{int mid = R-(R-L)/2;
if (query(i , mid) + i-1 >= 0) {h = mid; L = mid+1; continue;} R = mid-1;}
ANS += h-i+1
}

Here is my submission: https://codeforces.me/contest/1736/submission/175452764

shit

I think D and C2 indeed had the correct difficulty for the 4th and 5th problem; the only issue was their positions that confused participants. I'm pretty sure that if participants spent more time on D than C2, there would have been more solves for D.

satyam343, thanks for amazing problems and please fix broken \t{good} in the editorial of C1.

Am I the only one who receives RTE on test 4 for no reason? I tried modifing it with NMAX to 1e3, but it's a long long issue. If I change it in int it receives WA

https://codeforces.me/contest/1736/submission/175448716

Problem C1 ( Good Subarrays ) Easy O(N) Solution:

#include <iostream>
using namespace std;
int main(){
    int t;
    cin>>t;
    while (t--){
        int n, j=0;
        long long count=0;
        cin>>n;
        int a[n];
        for (int i=0;i<n;i++){ 
            cin>>a[i];
            count+=min(i-j+1, a[i]);
            j=max(j,i-a[i]+1);
        }
        cout<<count<<endl;
    }
    return 0;
}

E is pretty nice, it uses a very similar dp as this problem. link

For problem C1, I have a solution using Segment Tree to maintian the maximum value of a segment. share it. click here

My solution for C1:

Claim: If $$$a[l], a[l+1], ..., a[r]$$$ is a good subarray, then , for all $$$x, y$$$, such that $$$l \le x \le y \le r$$$, we have that $$$a[x], a[x+1], ... a[y]$$$ is a good subarray.

With that claim in mind, let's make a two pointers approach. For all $$$l, r$$$ that the interval $$$[l, r]$$$ is good, we have $$${r-l+2}\choose 2$$$ sub-intervals of $$$[l, r]$$$ that is good. So, lets make the following algorithm:

• Start with $$$l = 1$$$ and $$$r = 1$$$, and $$$antr = 0$$$ ($$$antr$$$ is the last $$$r$$$ that we compute for an answer).
• If $$$a[r] \ge r-l+1$$$ and $$$a[r+1] < r-l+2$$$, it means that $$$[l, r]$$$ is good and $$$[l, r+1]$$$ is not, then, lets add to our answer $$${r-l+2} \choose{2}$$$ $$$-$$$ $$${antr - l + 2}\choose{2}$$$, then make $$$antr = r$$$ and $$$l++$$$. See that, if $$$[l, r]$$$ is a solution, then $$$[l+1, r]$$$ also is, but we are counting $$$[l+1, r]$$$ two times, so, to avoid that, we are going to add a value for an answer if the $$$r$$$ is different. If it is the same, just do $$$l++$$$ and continue the algorithm (That means, don't update the answer and don't update $$$antr)$$$.
• Else, just make $$$r++$$$

Code: link

I think I have a simpler code for C2, in which I don't use any complex data structures except simple arrays.

#include <bits/stdc++.h>
using namespace std;

int n;
vector<int> arr, left_most, right_most, right_second_most;
void get_bound() {
    // left_most[i] represents the leftmost point such that subarray arr[left_most[i]:i] is good
    left_most.resize(n + 1);
    // right_most[i] represents the rightmost point such that subarray arr[i:right_most[i]] is good
    right_most.resize(n + 1);
    // right_second_most[i] is similar with right_most[i]
    // but when you start from i, and go right, you have one chance to skip bad point.
    right_second_most.resize(n + 1);
    for (int l = 1, r = 1, r2 = 1; l <= n; l++) {
        while (r <= n and arr[r] - r >= 1 - l) {
            left_most[r] = l;
            r++;
        }
        right_most[l] = r - 1;
        r2 = max(r2, min(r + 1, n + 1));
        while (r2 <= n and arr[r2] - r2 >= 1 - l) {
            r2++;
        }
        right_second_most[l] = r2 - 1;
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    arr.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> arr[i];
    get_bound();

    // S1: presum of contributions of all points
    // S2: presum of contributions of all points, if each of them has one skip chance.
    std::vector<long long> S1(n + 1);
    std::vector<long long> S2(n + 1);
    for (int i = 1; i <= n; i++) S1[i] = S1[i - 1] + (right_most[i] - i + 1);
    for (int i = 1; i <= n; i++) S2[i] = S2[i - 1] + (right_second_most[i] - i + 1);
    long long total = S1.back();

    int m;
    cin >> m;
    for (int i = 0; i < m; i++) {
        int p, x;
        cin >> p >> x;
        if (x == arr[p]) {
            cout << total << '\n';
        } else if (x < arr[p]) {
            int now_left_most = max(left_most[p], p - x + 1);
            if (now_left_most == left_most[p]) {
                cout << total << '\n';
                continue;
            }
            // now_left_most > left_most[p]
            // we can cut off contributions from left_most[p] to now_left_most-1.
            // but, they are not cut off completely. they can still reach p-1.
            long long cut_off = S1[now_left_most - 1] - S1[left_most[p] - 1];
            long long remain = (long long)((p - now_left_most) + (p - left_most[p] + 1)) * (now_left_most - left_most[p]) / 2;
            cout << total - cut_off + remain << '\n';
        } else {
            int now_left_most = max(int(lower_bound(right_most.begin() + 1, right_most.end(), p - 1) - right_most.begin() - 1) + 1, p - x + 1);
            if (now_left_most == left_most[p]) {
                cout << total << '\n';
                continue;
            }
            // now_left_most < left_most[p]
            // this is the time to use skip chance!
            // for all those points that stuck at p, they can skip p and reach right_second_most
            long long old_sum = S1[left_most[p] - 1] - S1[now_left_most - 1];
            long long now_sum = S2[left_most[p] - 1] - S2[now_left_most - 1];
            cout << total - old_sum + now_sum << '\n';
        }
    }
}

Here is an explaination for B I came up with Let a = {a1,a2,a3} b={b1,b2,b3,b4} Since a1 = gcd(b1,b2) => b1 and b2 are multiple of a1 similarly b2 and b3 are multiple of a2

Since b2 is multiple of a1 & a2 => b2 = k1 * lcm(a1,a2) (multiple of lcm) since b3 is multiple of a2 and a3 => b3 = k2 * lcm(a2,a3)

Now a2 = gcd(b2,b3) = gcd(k1*lcm(a1,a2) , k2*lcm(a2,a3)) = GCD GCD will be decided by lcm and multiple factors k1&k2 k1 and k2 can be used to multiply an integer to the gcd(lcm(a1,a2) , lcm(a2,a3))

From the above observation a[2] must be divisible by the GCD (we can set k1 and k2 to reach a[2])

Coulnt do this in contest :(

Link to submission

I code part of c1 why declaring dp with size n + 5 when n + 1 can also do the work.

Waiting for 1736E — Swap and Take Editorial!

Can anyone explain me what this code is doing ?

set<ll> found; found.insert(n+1);  
    sort(track.begin(),track.end()); 
    for(auto it:track){
        if(it.s.s){
            ll r=*found.upper_bound(it.s.f);
            ans[it.s.s]=pref[it.s.f-1]+dp[r]+sum[r-it.s.f]+(it.f+it.s.f-1)*(r-it.s.f);
        }
        else{
            ll r=*found.lower_bound(it.s.f); found.insert(it.s.f);
            dp[it.s.f]=dp[r]+sum[r-it.s.f]+(it.f+it.s.f-1)*(r-it.s.f);
        }
    }

In problem C2, what is the offline approach?

Regarding problem C2 : how to find such q ?

In the C1 Editorial, what do you mean by a[i−dp[i−1],i−1] and a[i−dp[i−1],i]? Array a is 1D array. But you used comma between the calculation of the array index.

In C1, how can we solve it using two pointers, why is this approach failing :

l = 0, r = 0
ans = 0
while(r < n)
   if s[r] >= (r -l + 1):
      r += 1
   else:
      length = r - l
      ans += length * (length-1) / 2
      while (a[r] < (r - l + 1)):
        l += 1
length = r - l
ans += length * (length - 1) / 2
print(ans) 

Is the algorithm mentioned in the editorial for C2 always correct?

Edit after reply: Yes, it is; I just misunderstood the track[i] definition :p

Take n = 10 and a = [8, 8, 8, 8, 8, 8, 1, 8, 8, 8].
Consider the query: p = 7, x = 10
The new a would be b = [8, 8, 8, 8, 8, 8, 10, 8, 8, 8].

dp[i] = min(dp[i-1] + 1, a[i])
adp[i] = min(adp[i-1] + 1, b[i])

dp:
dp[1] = 1
dp[2] = 2
dp[3] = 3
dp[4] = 4
dp[5] = 5
dp[6] = 6
dp[7] = 1
dp[8] = 2
dp[9] = 3
dp[10] = 4

adp:
adp[1] = 1
adp[2] = 2
adp[3] = 3
adp[4] = 4
adp[5] = 5
adp[6] = 6
adp[7] = adp[p] = 7
adp[8] = 8 = a[8]
adp[9] = 8 = a[9]
adp[10] = 8 = a[10]

Let q be the smallest index greater than p such that adp[q] = a[q]. So q = 8.

Indeed, adp[1] + adp[2] + ... + adp[p-1] = dp[1] + dp[2] + ... + dp[p-1].

However, adp[q] + adp[q+1] + ... + adp[n] = adp[8] + adp[9] + adp[10] = 24,
while dp[q] + dp[q+1] + ... + dp[n] = dp[8] + dp[9] + dp[10] = 9.
So, $$$\sum_{\ i=q}^{\ n} adp[i] \neq track[q]$$$!

To further increase my confusion, I ran the code for offline queries with this data and it gave me the right answer. (52)

Is there an error in the solution written in words? Is there an error in my understanding of the editorial? And how is the offline queries code different than the solution in words? (e.g. what is "dp" in the offline queries code, if "len[i] = min(len[i-1]+1, a[i])"?)

Any help would be appreciated!

For C2, Could you please explain how to find q both online and offline.

In C2, how can I find q (let q be the smallest index greater than p such that adp[q]=a[q])?

I find C2 pretty damn good, but would be better if they just get rid of C1 entirely and place C2 as E instead.

I have a way way simpler solution(online) for C2.

We can basically find out for each index i, if i is the start of a subarray, what are the first two bad points (bad points being points at which the given condition gets violated). We can do this in O(n) using queues (just observe monotonicity of bad points wrt starting points). Why is calculating only till the second point important? Because the only increase in answer for some start point happens when its first bad point gets resolved.

Now for each query, we can do some casework, and use prefix sums to calculate delta (this is the easy part so I wont go into it).

Implementation: link

Alternate solution for problem E which has same time complexity as the editorial solution, but uses only $$$O(n^2)$$$ memory:

Key observation:

In atleast one of the optimal solutions, the result of all swap operations can be viewed as the following:

• Some subset of elements $$$S$$$ will move.
• Each element in $$$S$$$ moves in the following manner- Element with index $$$i$$$ moves to the left till some point $$$L_i$$$ and then moves to the right till some point $$$R_i$$$. Finally all the points with indices between $$$L_i$$$ and $$$R_i$$$ will have $$$a_i$$$ added as their contribution to the score. (There are quite a few tiny observations to be made to prove this, so try it yourself)
• If $$$i$$$ and $$$j$$$ are indices which belong in subset $$$S$$$ and $$$i < j$$$, then $$$L_i < L_j$$$ (Note that $$$i < L_j$$$ may or may not hold).

So the array can be modelled as something like: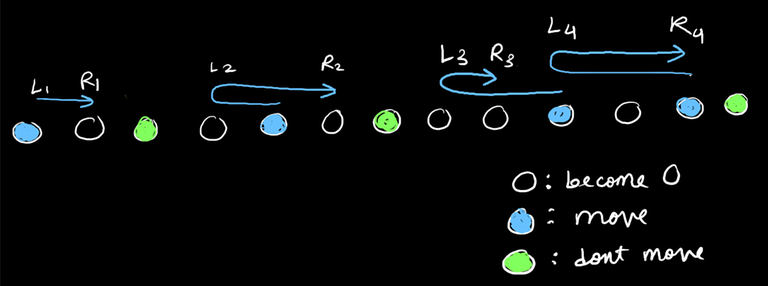

Coming up with DP States and Transitions:

Define the dp state as $$$dp[i][j]$$$, which holds maximum score we can get from the last $$$i$$$ elements, if we need to make atleast $$$j$$$ swaps before the $$$i$$$'th element to be able to transition from this state.

The transitions can be made in the following manner: Iterate over $$$i$$$ from $$$n$$$ to $$$1$$$, and then iterate over $$$L_i$$$ from $$$i$$$ to $$$1$$$, notice that all that really matters about the state which you transition from is its second parameter, so basically maintain an array which stores best possible transition for each value of second parameter, and keep trying to improve it as $$$L_i$$$ decreases.

Implementation: link

Nooby editorial for B

the number $$$b[i]$$$ ($$$i \neq 1$$$) is constrained to be a multiple of both a(i) and a(i-1). Thus, the smallest value that can be given to $$$b(i)$$$ = $$$LCM(a[i],a[i-1])$$$. Any value given to be $$$b[i]$$$ must be a multiple of this $$$LCM$$$. That is to say $$$b(i) \geq k\cdot LCM(a[i],a[i-1])$$$ for some $$$k \geq 1$$$

wishful thinking: maybe if setting $$$b[i]$$$'s equal to $$$LCM$$$ does not work, then no other answer can work out. Turns out this is true The risk with setting equal to $$$lcm$$$ is that the evaluated gcd might turn out bigger than the required gcd (the $$$a(i)$$$ value), but it is guaranteed to not turn out smaller than required.

proof-ish: since $$$b(i)$$$ is constrained to be a multiple of both $$$a(i)$$$ and $$$a(i-1)$$$, any value I assign to $$$b(i)$$$ must be a multiple of the $$$lcm(a(i),a(i-1))$$$.

What we can say about the evaluated $$$a(i) = gcd(lcm_1,lcm_2)$$$ is that it will be atleast equal to the required/intended $$$a(i)$$$ or more but never lesser, since $$$lcm_1$$$ and $$$lcm_2$$$ are atleast guaranteed to be multiples of required $$$a(i)$$$.

Suppose we set $$$b(i)$$$'s as the lcms. If the gcd of lcms is turning out greater than required. That means $$$gcd(lcm_1,lcm_2) = X > required$$$ then gcd of any other values assigned to b(i) will also turn out greater than required since b(i) must be a multiple of the lcm value. That is $$$gcd(k\cdot lcm_1, l\cdot lcm_2) = gcd(k,l)\cdot gcd(lcm_1,lcm_2) \implies gcd(k,l)\cdot X$$$

Thus, if answer does not exist from setting $$$b(i) = lcm(a(i), a(i-1))$$$ recursively. Then, no answer exists anyways.

Handle case $$$b(0)$$$ and $$$b(n)$$$ separately.

What is second best approach for Problem D ? If One is unable to get the idea of claim ?

Alternative way to solve C2 (actually it is pretty similar to the editorial):

First we need to talk about C1. Let $$$dp_i$$$ is the first position to the left of $$$i$$$ such that $$$a_{dp_i}, a_{dp_i + 1}, ..., a_i$$$ is invalid. Then $$$dp_i = max(dp_{i - 1}, i - a_i)$$$. The answer to C1 is sum of $$$i - dp_i$$$ for all $$$1 \leq i \leq n$$$, or $$$n \cdot (n + 1) / 2 - \sum_{i = 1}^{n} {dp_i}$$$. Submission for C1. If you notice, the $$$dp$$$ array is actually the prefix maximum of $$$i - a_i$$$ for each $$$i$$$. So I use an array $$$b$$$ with $$$b_i = i - a_i$$$ for future usage in C2.

Now turn to C2. Let's call $$$pref_i$$$ is the prefix sum of $$$dp_i$$$, and $$$suf_i$$$ is the sum of $$$\sum_{i = j}^{n}{dp[i]}$$$ supposed we start calculating $$$dp$$$ from $$$j$$$ (this is actually similar to the $$$track$$$ array in editorial, but with a different definition). Calculating $$$suf$$$ can easily be done by monotonic stack with the help of array $$$b$$$. Now, for each query, applying $$$a_p = x$$$ equivalents to changing $$$dp_i = max(dp_{i - 1}, p - x) = d$$$. Then $$$d$$$ will propagate among our $$$dp$$$, and we want to find the first position $$$q$$$ such that $$$d$$$ stops propagating at $$$q - 1$$$. For example, if $$$dp = [0,0,2, 3, 3, 3, 4, 6, 7]$$$ and we want to change $$$dp_5 = d = 5$$$, then $$$q = 8$$$ and our new $$$dp$$$ will be $$$[0,0,2,3,5,5,5,...,...]$$$. Here we can't assure that the last two elements in $$$dp$$$ are $$$6$$$ and $$$7$$$ after the change, but we can calculate the sum of those $$$'...'$$$, and it actually is $$$suf_q$$$. So, the sum of $$$dp$$$ after the change will be: $$$\sum{dp} = pref_{p - 1} + d * (q - p) + suf_{q}$$$, and answer for each query is: $$$n \cdot (n + 1) / 2 - \sum{dp}$$$.

To find the position $$$q$$$, I use binary search and max range query using sparse table. Hence the time complexity will be $$$O(nlogn)$$$. Submission to C2

Is it possible to solve D without rotations in polynomial time?