stould's blog

Hi, working with Tree.
By stould, 11 years ago, In English

Hello everyone.

I have a graph in the shape of a tree, in which I need to know the following:

  • 1) L = Lowest common ancestor between vertex A and B.
  • 2) The edge of lower cost between A and L, and lower cost edge between B and L.

I can not think of an efficient way to make the item 2), anybody could give me a light?

My naive ideia is to every query check all vertex between A ~ L and B ~ L, but it is slow.

If you need code, I can show my code here. Thank you.

Tags lca
  • Vote: I like it
  • +3
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

You mean the lowest cost, not lower.

You just need to augment the standard LCA preprocessing. To find LCA, you remember for every vertex its ancestors at distances 2i, and the depth of every vertex below the root. It's a well-known algorithm. To find the cheapest edge, you can remember also the cheapest edge on the path from a vertex to its ancestor at distance 2i, along with that ancestor. As the LCA algorithm "cuts" the paths from A to L and from B to L into smaller paths, you can just calculate the minima from the (pre-calculated) cheapest edges on those smaller paths.

The time complexity is the same as of this LCA algorithm — .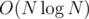

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sorry for my poor english. Wow, thank you for the explanation, I'll try to implement it. :)

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In addition to the method outlined by Xellos, there is another standard algorithm that can be used for this question. Heavy-Light decomposition

→ Reply