→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 11:01:19 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Can we submit our solutions after the contest?
Yeah, you just have to wait for a while. When you know your score, there's an "analysis mode" and you can submit again for practice.
Thank you
Damn, got stuck for like 90 minutes on the fourth problem, while the fifth was a piece of cake to solve :(
How to solve it?
Let the height of a strip be 1. The cuts are at heights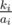 , for 0 < ki < ai, and we want the number of distinct fractions among those.
, for 0 < ki < ai, and we want the number of distinct fractions among those.
Let there be a fraction , with coprime x, y and x < y. If there's
, with coprime x, y and x < y. If there's 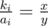 , then
, then 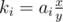 must be an integer; for coprime x, y, it means that y divides ai; this condition is also sufficient, and the number of satisfying x for the given y is φ(y).
must be an integer; for coprime x, y, it means that y divides ai; this condition is also sufficient, and the number of satisfying x for the given y is φ(y).
That means we need to sum up φ(y) for all distinct divisors y of at least one ai. For sufficiently small ai, computing φ(y) for all 1 ≤ y ≤ 100000 is easy, and to check a divisor's existence, we can use an array of bools denoting the existing values of ai and try the multiples of every y.
But yeah, 4 and 5 should've been swapped. I think I spent about an hour or more on this.
I also have similar solution, except when computing the number of distinct irreducible ( removed ) fractions, I just used O(N^2 * log N) precomputation and then just pasted the array in the code, since the limit is 1 MB.
Coprime x, y means irreducible fraction.
Precomputation: nice! It'd be funny if some future problem of COCI could be solved in O(1) like this :D
Oh, OK, sorry, I misread the first paragraph, I thought it was needed mentioning there as well.
But yeah, I was surprised when I found out the source limit is 1 MB, usually it's limited by 100 KB.
Why can't we simply use this f(a * b) = f(a) * f(b) for coprime a and b? Am I missing something?
Also we can count number of irreducible fractions using Inclusion–exclusion principle. My code
I think this problem (problem D) is similar to SGU 370.
Oh yeah, 618 points! My best result so far, ever!
Short ideas of some tasks:
SUMO: binsearch the smallest k such that the graph formed by the first k edges isn't bipartite; bipartiteness can be checked with BFS
UTRKA: DP on (number of edges,vertex i,vertex j) gives the maximum advantage (can be negative) out of all paths from i to j, stopping the computation when there's a negative cycle and only adding edges to existing paths gives me 80% of points
COKOLADE: there only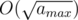 ways of how the array of "candies per capita" can look; iterate over the smallest k-s corresponding to them — for a given k, find the smallest k' > k such that some
ways of how the array of "candies per capita" can look; iterate over the smallest k-s corresponding to them — for a given k, find the smallest k' > k such that some 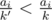 ; for a given k, only the tables with equal
; for a given k, only the tables with equal 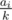 (candies per capita, integer division) socialize
(candies per capita, integer division) socialize
I have O(n3 * log2(n)) for last problem (pretty sure it is solvable in O(n3 * log(n))) time. I have 80% of points for this problem as well.
Let i-th edge's weight be m[i]-s[i]. So we have to find shortest cycle with negative weight in this graph. Lets precalculate all minimal distances for n=1,2,4,8,16... edges using Floyd-Warshall algorithm. Then let's do binary search by the answer. Using precalculated information we can find shortest disctances between every pair of vertexes with exactly M edges between them in O(n3 * log(n)) time. If distance from i to i is negative for some i, than we have cycle of negative weight for current value of M.
And for the reference, if you just use matrix multiplication, incrementing the size by 1 (so no need for binary search), you get 70% of points. Which seems quite a lot.
How do you assume if there is a negative cycle with lenght M there have to be with lenght M + 1?
There probably is some misunderstanding.
If distance from i to i is negative for some i, than we have cycle of negative weight for current value of M.In this sentence I meant, that we have cycle with length not greater than M. If we have negative cycle with length M, than, obviously, shortest distance from i to i will be negative also for values bigger than M.
Also, SUMO can be solved with DSU. For each component c, store the number of a component that should be colored in a different color than this component in adj[c]. Suppose an edge (a, b) comes in. If group(a) = group(b), then we output the number of the current edge. Otherwise merge group(adj[a]) with group(b), and group(adj[b]) with group(a).
I think binsearch is the simplest solution for this. At least, I don't see any completely obvious greedy solution, although that was my initial guess. DSU is just unnecessarily much to code.
No, not at all: http://ideone.com/OIgU8Y.
Challenge accepted: http://ideone.com/wcbbCN
You may have fewer lines, but those lines are much more complicated.
It might look complicated, but it's based on a BFS, which is really simple to code when you know it (which probably anyone does before DSU). I also don't use typedefs and extensive defines, and don't put every variable in a static array, which would probably make it clearer, but I wouldn't be able to write it instantly.
I'm not talking about lines — if I wanted to, I could cut down on them significantly, and so could gen on his. If you look at any BFS I've coded, it looks like this (with the "part" array and the few operations with it added). If you look at any binsearch I've coded, it also looks like this, and same with reading+graph construction in my codes. And I don't copy-paste.
agree with Chortos-2 and besides it is also worth mentioning that at least I have DSU prewritten.
upd: and also, BS is notoriously tricky XD
Imagine you go to a competition where pre-written code is not allowed. You can solve the problem in theory, but coding it takes too long or you make mistakes there, and so you can't solve the problem in question. Moral lesson: prewritten code = potential fail.
On the other hand, why not have pre-written binsearch, too, if it's so tricky? You pose a problem and one solution in your post. And once again, if you can write it quickly and correctly in any situation, it's not tricky.
I'm not saying people should write codes the same way I do. Everyone has their own style, but if you're able to instacode basic algorithms, it can give you a large edge.
Actually I have prewritten BS too
http://pastebin.com/MLXTSmuv
But, in fact I am not the "script-kiddie" kind of man :D. I don't use prewritten codes any more (excluding on CF and TC maybe where rating kinda matters). What I meant by my previous comment was that DSU is one of the data-structure you can type w/o thinking and quickly, while BS needs a special treatment (for me).
Lastly, I think ur right, for ambitious algorist implementation should be of no problem.
I guess it varies from person to person. Binsearch is just about getting the ± 1 correct, which is easy if you use half-open intervals, and it's short. When coding DSU, I still need to think for a while sometimes.
I agree with Xellos. By the way, I haven't thought about binsearch at all, so at the time was wondering why they have put DSU in the first place in a COCI contest.
Is DSU that unusual for COCI?
DSU was my second idea (first was an obvious greedy, which, as I soon realized, was obviously wrong :D), but it seemed strange for a 3rd problem, so I tried to find some other way to solve it.
No, I mean, it is only a 100p problem on a high school contest, surely it should not require any advanced algorithm. ;D
True that. DSU is not really hard, but still.
i think gen's DSU solution is very shorter than your binary search code.
I believe that binary search is the tougher way to go, I tried to think of a binary search solution in the beginning but I couldn't find any, thumbs up for your idea I really liked it! I ended up coding a DSU solution and I don't even complete scanning the input when I get the answer :D :D
http://ideone.com/ud4foP
UTRKA for 100%:
Let D(i, j, k) be maximum advantage out of all paths from i to j using at most k edges.
If we know D(i, j, h) for some h and each i, j and we also know D(i, j, l) for some l and each i, j, we can compute D(i, j, h + l) in O(n3) time.
At first we compute D(i, j, k) for k equal to powers of two and after that we construct binary representation of the optimal k digit by digit (starting with most significant digits).
Total time complexity is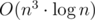
After computing D for all powers of two, how do you search for the optimal k?
Got full score in upsolving with this idea:
1) Calculate D for all powers of 2.
2) Calculate D for all powers of 2 decreased by 1 (lets call this array Prefix).
3) Find the smallest i, that Prefix[i] contains negative cycle. Out current answer is 2a - 1, where a == i+1
4) Lets try not to use some particular bit in our current answer (from the most valuable to less valuable). For this we will keep track of our current suffix. Suppose we are looking for i-th bit. We need to join our current suffix and Prefix[i-1]. If the result of join contains negative cycle — we do not use i-th bit, otherwise — we use it and update current suffix.
My code is ugly, but maybe it will be helpful.
In fact, I search for optimal k - 1 (that is, the maximum number such that there is no negative cycle using this number of edges, or less). What I do is binary search, where I keep D for actual lower bound. In the beginning my lower bound is 0 and upper bound is the smallest power of two U, such that there is a negative cycle with U (or less) edges. Therefore the size of interval where I search is power of two and it always will be (as it halves in each iteration).
The number W in the middle of my interval is lower bound + some power of two, so I can compute D for W in O(n3) using Ds for lower bound and for that power of two. If there is a negative cycle using at most W edges, we can set upper bound to W. Otherwise we can set lower bound to W. We have already computed D for W, so we still know D for our lower bound.
i think the problem Utrka was very similar to 147B - Smile House
Yeah, it is. Just the time limit is larger. But that one seems quite difficult, too — less than 200 successful solutions.
i don't solve this problem because i read the problem after the end of contest. :(
in the next contest i will do what Sereja always recommend (reading ALL the problems)
Can anyone explain the solution of task "cokolade" ? My solution is sqrt(10^8) * 100, I simply consider all the divisors of the numbers, but this seems incorrect!
Before asking a question, check if it's been answered already. For example here
If this doesn't work for you, you're coding it wrong.
Thanks for replying, I'll check your comment.
I'm not allowed to log in from my location. Is there any other way I might participate?
I guess you are trying to log into "HONI 2013./2014. — 4.kolo". Try logging into "COCI 2013./2014. — Round #4".
i m asking this question to who used this idea(described below) while binary search. I and Fcdkbear could not come up with answer. Here is question :
Why dist[i][i] with using exactly M edges have to be less then using exactly M — 1 edges. I'm talking abouth coci last problem.
Could you please look that example :
if we have 4 nodes and this edges between them :
1 to 2 with -1 weight
2 to 3 with -1 weight
3 to 1 with -1 weight
2 to 4 with 1000 weight
4 to 3 with 1000 weight
when M = 3 dist[1][1] = -3 and when M = 4 dist[1][1] = 1998