Hockey Stick Identity — easy explanation
In this post I explain what Hockey Stick Identity (also reffered to as parallel summing) is, visualize it and present an intuitive 'proof'.
What is Hockey Stick Identity?
For whole numbers $$$n$$$ and $$$r$$$ $$$(n \geq r),$$$
Let's visualize this on the Pascal triangle for $$$n = 6, r = 2$$$. We know that elements on the triangle are results of the binomial coefficient. For example $$$ \binom{6}{2} = 15 $$$ is in $$$\color{blue}{\text{row}}$$$ $$$6$$$, $$$\color{orange}{\text{column}}$$$ $$$2$$$.
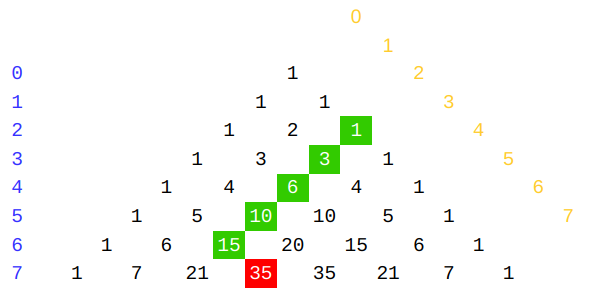
Do you see it? It resembles a hockey stick! Hence the name.
\color{green}{ \sum\limits_{k=2}^{6} \binom{k}{2} } &= \color{red}{ \binom{6+1}{2+1} } \\ \color{green}{ \binom{2}{2} + \binom{3}{2} + \binom{4}{2} + \binom{5}{2} + \binom{6}{2} } &= \color{red}{ \binom{7}{3} } \\ \color{green}{ 1 + 3 + 6 + 10 + 15 } &= \color{red}{ 35 } \end{align} $$$
'Proof'
Idea for this part has been very kindly suggested by my friend hugo4CF.
Let's say we have $$$n + 1 = 7$$$ letters $$$(A, B, C, D, E, F, G)$$$ and we want to count all possible sets of $$$r + 1 = 3$$$ letters from it. The answer to this is obviously $$$\displaystyle \binom{7}{3} = 35$$$. That is the right side of our equation. But we can count it differently. Let's put our letters in a row (the order doesn't matter), e. g.: $$$(E, G, A, D, F, B, C)$$$. Now for each $$$k \in \lbrace r, r + 1, \dots, n \rbrace = \lbrace 2, 3, 4, 5, 6 \rbrace$$$ we will take the $$$\color{magenta}{k+1}$$$-st letter and choose the remaining $$$r = 2$$$ letters from the first $$$k$$$ letters. Let's visualize it:
| k | row of letters | result |
|---|---|---|
| 2 | ($$$\underbrace{\textbf{E, G}}_{\binom{2}{2}}, \color{magenta}{\textbf{A}}$$$, D, F, B, C) | $$$\displaystyle\color{green}{\binom{2}{2}}$$$ |
| 3 | ($$$\underbrace{\textbf{E, G, A}}_{\binom{3}{2}}, \color{magenta}{\textbf{D}}$$$, F, B, C) | $$$\displaystyle\color{green}{\binom{3}{2}}$$$ |
| 4 | ($$$\underbrace{\textbf{E, G, A, D}}_{\binom{4}{2}}, \color{magenta}{\textbf{F}}$$$, B, C) | $$$\displaystyle\color{green}{\binom{4}{2}}$$$ |
| 5 | ($$$\underbrace{\textbf{E, G, A, D, F}}_{\binom{5}{2}}, \color{magenta}{\textbf{B}}$$$, C) | $$$\displaystyle\color{green}{\binom{5}{2}}$$$ |
| 6 | ($$$\underbrace{\textbf{E, G, A, D, F, B}}_{\binom{6}{2}}, \color{magenta}{\textbf{C}}$$$) | $$$\displaystyle\color{green}{\binom{6}{2}}$$$ |
This way we get our left side of the equation.
Application
This identity is used in problem 660E - Different Subsets For All Tuples. Leave a comment if you know other problems for it.
In practice
Naturally, if we want to calculate the binomial, we can for example use the formula $$$ \displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)!} $$$ and do the division using modulo-inverse.











A recent problem that uses this identity.
Mr Chesca would be proud!