Hi everyone! Today nor sir and I would like to talk about generating uniform bracket sequences. Over the past few years when preparing test cases, I have had to generate a uniform bracket sequence a few times. Unfortunately I could not figure out how, so I would like to write a blog about this now. Hopefully this blog would be useful to future problem setters :) Scroll down to the end of the blog to copy our generators.
First, let's define some things. A bracket sequence is a string with $$$n$$$ $$$\texttt{(}$$$ s and $$$n$$$ $$$\texttt{)}$$$ s. A balanced brackets sequence is a bracket sequence with the additional constraint that it becomes a valid arithmetic expression when we add some $$$\texttt{1}$$$ s and $$$\texttt{+}$$$ s. Let $$$p$$$ be the prefix sum array of a bracket sequence (we assign $$$1$$$ to $$$\texttt{(}$$$ and $$$-1$$$ to $$$\texttt{)}$$$ and take the prefix sum). For example, if our bracket sequence is $$$\texttt{())()((())}$$$, then $$$p=[1,0,-1,0,-1,0,1,2,1,0]$$$.
An alternate way to think about the prefix sum is to imagine the bracket sequence as a sequence of increasing and decreasing lines.
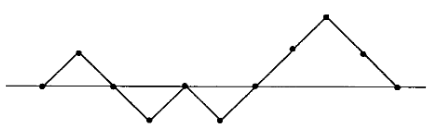
We can see that the necessary and sufficient for a bracket sequence to be balanced is that all elements of the prefix sum is non-negative.
Let's define the badness of a bracket sequence as the number of lines in the above diagram that is below the $$$0$$$-line. So, the badness of our bracket sequence is $$$4$$$.
Let's call a bracket sequence irreducible if the line touches the $$$0$$$-line exactly twice (once at the start and at the end). So, $$$\texttt{(())}$$$ and $$$\texttt{))()((}$$$ are both irreducible but not $$$\texttt{()()}$$$. It is natural to also define a irreducible decomposition of a bracket sequence. $$$\texttt{())()((())}$$$ gets decomposed into $$$\texttt{()}$$$,$$$\texttt{)(}$$$,$$$\texttt{)(}$$$,$$$\texttt{(())}$$$.
Now, we want to note that all irreducible bracket sequences are either balanced or are some sort of "inverse" of a balanced bracket sequences. By inverse, we can either reverse the entire string or flip every bracket in the string. Please note that these are different.

For example, $$$\texttt{)))(()((}$$$ can be turned into $$$\texttt{((())())}$$$ by flipping every bracket or $$$\texttt{(()(()))}$$$ by reversing the substring.
Firstly, let's start with finding a recursive formula for the Catalan numbers. One of the basic recurrences when dealing with bracket sequences is to decompose them into the form of $$$\texttt{(}X\texttt{)}Y$$$, where $$$X$$$ and $$$Y$$$ are both valid bracket sequences (they might be empty). This decomposition is actually unique since $$$\texttt{(}X\texttt{)}$$$ can only be our first term in our irreducible decomposition (for us competitive programmers, think of it as dp where our transition is removing the first irreducible substring). We immediately have the recurrence $$$C_{n+1} = \sum\limits_{i=0}^n C_i C_{n-i}$$$ for $$$n > 0$$$ and a base case of $$$C_0=1$$$ for $$$n=0$$$. After some manipulation with formal power series $$$[1,2 \text{ example } 2.3.3]$$$, you can find that we get the familiar $$$C_n = \frac{1}{n+1} \binom{2n}{n} = \frac{1}{2n+1} \binom{2n+1}{n}$$$.
Mapping 1
Let's take a look at $$$C_n = \frac{1}{2n+1} \binom{2n+1}{n}$$$ first. What other sequence can we get the $$$\binom{2n+1}{n}$$$ term from? Well, the number of binary strings with $$$n$$$ $$$\texttt{(}$$$ s and $$$n+1$$$ $$$\texttt{)}$$$ s. And nicely enough, $$$2n+1$$$ is the length of said binary string. Let's define the equivalence class $$$\sim _R$$$ where $$$s\sim_Rt$$$ when $$$s$$$ is a cyclic shift of $$$t$$$. Generally for binary strings, it is not so easy to count the number of elements in someone's equivalence class when we define it this way. But since $$$\gcd(2n+1,n)=1$$$ here, all cyclic shifts of a string are distinct and there are exactly $$$2n+1$$$ strings in any equivalence class. We are almost at a bijection to Catalan numbers already! We just need to show that there is a bijection between equivalence classes and balanced bracket sequences.
Lemma
Given a string of $$$n$$$ $$$\texttt{(}$$$s and $$$n+1$$$ $$$\texttt{)}$$$s, there exists exactly $$$1$$$ cyclic shift where the first $$$2n$$$ elements is a valid bracket sequence.
As an example, consider the bracket sequence $$$\texttt{)())(()}$$$. The only cyclic shift that gives us a prefix sum with our condition is $$$\texttt{(())())}$$$.
The proof of this is not too hard and you should prove it yourself, but for completeness, I will put it here.
We can see that in each equivalence class, there is exactly a single element whose first $$$2n$$$ elements are a balanced bracket sequence. Let this be the representative of the equivalence class. We can obtain balanced bracket sequences from representatives by removing the last character and vice versa by appending a $$$\texttt{)}$$$. Therefore, there is a bijection between the equivalence classes and
There is a interesting problem which is related to this $$$[4]$$$ (in Chinese).
Mapping 2
Thank you nor sir for writing this part and independently discovering it.
The mapping mentioned here was, unfortunately, already present in literature $$$[5]$$$ after we checked, and my old proof was quite similar to the one mentioned in the paper. It used the Chung-Feller theorem, which says that the badness of bracket sequences is uniformly distributed (i.e., there are an equal number of strings for each value of badness), and then showed that the mapping was in fact a bijection from the set of strings of a fixed badness to the set of balanced bracket sequences.
However, I came up with a much simpler proof which we will present below along with the intuition behind the construction (we could not find this proof anywhere, so if anyone finds a reference, please let us know in the comments).
The main idea behind what we will do below is the identity $$$C_n = \frac{1}{n + 1} \binom{2n}{n}$$$. We try to construct a balanced bracket sequence from a bracket sequence with $$$n$$$ opening brackets and $$$n$$$ closing brackets, and then try to show that this construction is in fact an $$$n + 1$$$ to $$$1$$$ mapping from $$$S_n$$$ (the set of bracket sequences with $$$n$$$ opening brackets and $$$n$$$ closing brackets) to $$$S^*_n$$$ (the set of balanced bracket sequences of length $$$2n$$$).
The first idea is to note that, as mentioned earlier, if a string $$$S = AB$$$, where $$$A$$$ is the irreducible prefix of $$$S$$$, then we can make $$$A$$$ an irreducible balanced bracket sequence by either flipping all brackets of $$$A$$$ (which corresponds to flipping the corresponding diagram in the $$$x$$$-axis) or by reversing the string $$$A$$$ (which corresponds to rotating the diagram $$$180^\circ$$$).
The first attempt at finding a mapping was to do this: set $$$f(S) = A'f(B)$$$, where $$$A'$$$ is the string obtained by flipping all brackets in $$$A$$$ (or just reversing $$$A$$$). However, this will not give us a uniformly random way of constructing balanced bracket sequences, since $$$\texttt{((()))}$$$ is the image of $$$2$$$ strings under this mapping, and $$$\texttt{()()()}$$$ is the image of $$$8$$$ strings under this mapping.
So here was the crucial idea: we try to offset this asymmetry by modifying how we handle the case when $$$A \ne A'$$$. In this case, $$$A =\; \texttt{)}C\texttt{(}$$$ for some $$$C$$$, i.e., $$$S = \texttt{)}C\texttt{(}B$$$. So in order to try to compensate for the imbalance in distribution, we use $$$\texttt{(}f(B)\texttt{)}C'$$$ instead (where $$$A' = (C')$$$). As it turns out, this works out perfectly.
Here's the formal construction:
Definition: $$$f: \cup_{n = 0}^\infty S_n \to \cup_{n = 0}^\infty S^*_n$$$ is defined as
- $$$f(\varepsilon) = \varepsilon$$$, where $$$\varepsilon$$$ is the empty string.
- $$$f(AB) = Af(B)$$$, if $$$A$$$ is irreducible and balanced.
- $$$f(AB) = (f(B))C'$$$, if $$$A$$$ is irreducible and not balanced, and as a corollary, $$$A =\; )C($$$ for some $$$C$$$.
Claim: For any string $$$S^* \in S^*_n$$$, there are exactly $$$n + 1$$$ solutions to $$$f(S) = S^*$$$ for $$$S \in S_n$$$.
Proof: Let $$$S^* = A^*B^*$$$, where $$$A^*$$$ is the irreducible prefix of $$$S^*$$$. Let $$$S \in S_n$$$ be a string satisfying the equation $$$f(S) = S^*$$$. We prove this by induction. For $$$n = 0$$$, there is nothing to prove. Let's suppose $$$n > 0$$$. Then $$$S$$$ can be mapped to $$$S^*$$$ by using one of the two rules, depending on whether the irreducible prefix of $$$S$$$ is a balanced bracket sequence or not:
- Let $$$S = AB$$$, where $$$A$$$ is a balanced irreducible prefix of $$$S$$$. Then we must have $$$S^* = f(S) = A f(B)$$$. Since $$$A, A^*$$$ are both balanced irreducible prefixes of $$$S^*$$$, they must be equal, and $$$B^* = f(B)$$$. The number of solutions in this case is hence equal to $$$\frac{|B^*|}{2} + 1$$$ by the induction hypothesis.
- Let $$$S = AB$$$, where $$$A$$$ is not balanced, but an irreducible prefix of $$$S$$$. Then $$$A =\; \texttt{)}C\texttt{(}$$$, and $$$A' = \texttt{(}C'\texttt{)}$$$ (as mentioned above). By definition, $$$S^* = f(S) = \texttt{(}f(B)\texttt{)} C'$$$. By an analogous argument as above, since $$$f(B)$$$ is balanced, $$$A^* = \texttt{(}f(B)\texttt{)}$$$ and $$$B^* = C'$$$. There are exactly $$$\frac{|A|^*}{2}$$$ solutions as earlier.
Overall, there are $$$\frac{|A^*| + |B^*|}{2} + 1 = n + 1$$$ solutions to $$$f(S) = S^*$$$, as needed.
In fact, if, in the proof, we also keep track of the badness of the strings that generate a given balanced bracket sequence, we can see that there is one input string for each possible value of badness (and this gives an alternative proof of the Chung-Feller theorem).
Generating Balanced Bracket Sequences
It has been asked before on CodeForces $$$[6]$$$ how to generate a random bracket sequence. Judging from the comments, no one has been able to figure out how to generate it quickly (i.e. in linear time). So I will provide the code to generate a uniform balanced bracket sequence. Additionally, I will provide code that generates a random binary tree of $$$n$$$ vertices to balanced bracket sequences of size $$$2n$$$.
I know that there is also a bijection between bracket sequences and ordered trees, but there are better ways to generate a tree $$$[7]$$$. Also, there is also a bijection to full binary tree of $$$2n+1$$$ vertices, but there is a easy bijection to binary trees of $$$n$$$ vertices noting that the full binary tree of $$$2n+1$$$ vertices has $$$n+1$$$ leaf nodes. We simply remove all leaves, which leaves (pun not intended) us with a binary tree of $$$n$$$ vertices. So the binary tree is the "internal nodes" of the full binary tree.
Also, there is a (rather inelegant) method of generating balanced bracket sequences without using any of the techniques discussed earlier.
One of the first ideas that anyone attempting this task might have is to randomly place $$$\texttt{(}$$$ or $$$\texttt{)}$$$ in a string unless it is impossible to do so. However, we do not get a uniform distribution. Instead, let us vary the probability that we place $$$($$$ or $$$)$$$ in accordance to the actual probability that we will see in our required distribution.
Let $$$C_n^k$$$ denote the number of bracket sequences of size $$$2n$$$ with the first $$$k$$$ elements being $$$\texttt{(}$$$. From $$$[8]$$$, we know that $$$C_n^k = \frac{k+1}{n+1} \binom{2n-k}{n-k} = \frac{k+1}{2n-k+1} \binom{2n-k+1}{n-k}$$$. We can actually prove it using the same technique of adding a single $$$\texttt{)}$$$ and performing rotations.
Ok, so if we want to make a balanced bracket sequence of length $$$2n$$$ and we currently placed $$$a$$$ $$$\texttt{(}$$$s and $$$b$$$ $$$\texttt{)}$$$s, then there are $$$C_{n-b}^{a-b}$$$ possible balanced bracket sequence that have our current string as a prefix. Out of them, $$$C_{n-b}^{a+1-b}$$$ have the next character being $$$\texttt{(}$$$. So we simply calculate the probability that we should put $$$\texttt{(}$$$ as $$$\frac{C_{n-b}^{a+1-b}}{C_{n-b}^{a-b}} = \frac{n-a}{2n-a-b} \cdot \frac{a-b+2}{a-b+1}$$$. Notice that $$$n-a$$$ and $$$n-b$$$ are the remaining numbers of $$$\texttt{(}$$$ s and $$$\texttt{)}$$$ s respectively. The $$$\frac{n-a}{2n-a-b}$$$ term nicely corresponds to the ratio of $$$\texttt{(}$$$ s in the remaining characters.
As for the bijection from balanced bracket sequences to binary trees, remember earlier when we showed the recurrence $$$C_{n+1} = \sum\limits_{i=0}^n C_i C_{n-i}$$$ by bijecting into pairs $$$(X,Y)$$$ such that string is of the form $$$\texttt{(}X\texttt{)}Y$$$. This bijection works for a recursive bijection into binary trees too $$$[\text{folklore}]$$$. That is, $$$\texttt{()}$$$ bijects to the binary tree with $$$1$$$ nodes, then for any other bracket sequence, $$$X$$$ describes the left child and $$$Y$$$ describes the right child.
Ok enough talking, here are the codes (I used testlib $$$[7]$$$). They are written by both nor sir and I.
A Surprisingly Fast Generation
Thanks to pajenegod for pointing out that this method might be faster than $$$O(n^2)$$$.
Let us return to the original reccurence of $$$\texttt{(}X\texttt{)}Y$$$. This gives us a natural DnC-esque recurence if we are able to determine how to uniformly choose the correct size for $$$X$$$ and $$$Y$$$. Recall that $$$C_{n+1} = \sum\limits_{i=0}^n C_i C_{n-i}$$$ and that we have the approximation $$$C_n \approx \frac{4^n}{\sqrt{\pi n^3}}$$$ $$$[1]$$$.
For some bracket sequence of size $$$2(n+1)$$$, the probability we recurse into $$$X$$$ of size $$$s$$$ is $$$P_s = \frac{C_{s}C_{n-s}}{C_{n+1}}$$$. Of course, we are not able to store $$$C_n$$$ directly, but using the earlier approximation earlier, it makes sense to store $$$C'_n = \frac{C_n}{4^n}$$$, which should be at a reasonable size to use doubles. We can calculate $$$C'_{n+1} = \frac{n+\frac{1}{2}}{n+2} \cdot C'_n$$$ in linear time. Nicely, $$$P_s = \frac{C'_{s}C'_{n-s}}{4 C'_{n+1}}$$$.
Here, we can already bound these types of reccurences by $$$O(n \log n)$$$ if we don't care about the distribution of $$$s$$$ that we recurse to. We can do this by mapping $$$P_s$$$ in the order of $$$P_0,P_n,P_1,P_{n-1},\ldots$$$. That is, we generate a random number in $$$Z=[0,1)$$$. If $$$Z < P_0$$$, we recurse with $$$s=0$$$, if $$$Z < P_0+P_n$$$, we recurse with $$$s=n$$$, etc.
With this method, our time complexity is actually $$$T(n)=O(\min(a,b))+T(a)+T(b)$$$. So, we have $$$T(n)=O(n \log n)$$$.
But maybe we can do better. Note that the true complexity is $$$T(n+1) = \sum\limits_{s=0}^{n} P_s \cdot (T(s) + T(n-s) + O(\min(s,n-s))$$$
Let's look at the distribution of $$$P_s$$$ for $$$n=8$$$.
| $$$P_0$$$ | $$$P_1$$$ | $$$P_2$$$ | $$$P_3$$$ | $$$P_4$$$ | $$$P_5$$$ | $$$P_6$$$ | $$$P_7$$$ |
|---|---|---|---|---|---|---|---|
| $$$0.3$$$ | $$$0.092$$$ | $$$0.059$$$ | $$$0.049$$$ | $$$0.049$$$ | $$$0.059$$$ | $$$0.092$$$ | $$$0.3$$$ |
We see that the distribution is symmetric (which isn't that important) and that larger values appear on the extreme ends (which is important). This suggests in most cases, our recursion will make one side much smaller than the other.
Let us try to find an approximation for expected value of $$$\min(s,n-s)$$$ when drawn over the probability distribution of $$$P_s$$$. Note that $$$P_s = \frac{C'_{s}C'_{n-s}}{4 C'_{n+1}} \approx \frac{\sqrt{n^3}}{4 \sqrt{\pi s^3(n-s)^3}}$$$.
When $$$s \leq \frac{1}{2} n$$$, we get $$$P_s \lessapprox \frac{\sqrt{8}}{4 \sqrt{\pi s^3}} = \frac{1}{\sqrt{2 \pi}} \cdot \frac{1}{\sqrt{s^3}}$$$.
So, I thought the reccurence was going to look like $$$T(n)=O(\sqrt n) + T(\sqrt n) + T (n - \sqrt n)$$$. Which gives us $$$T(n) = O(n \log \log n)$$$. But unfortunately, this turned out to not be true.
After empirical testing and explicitly calculating the theoretical value of $$$T(n)$$$, I have observed that the actual complexity is $$$O(n \log n)$$$. I think it is quite interesting that despite our recurrence usually cutting at values of around $$$\sqrt n$$$, we end up having a total complexity of $$$O(n \log n)$$$ anyways, but probably with a significantly large logarithm base.
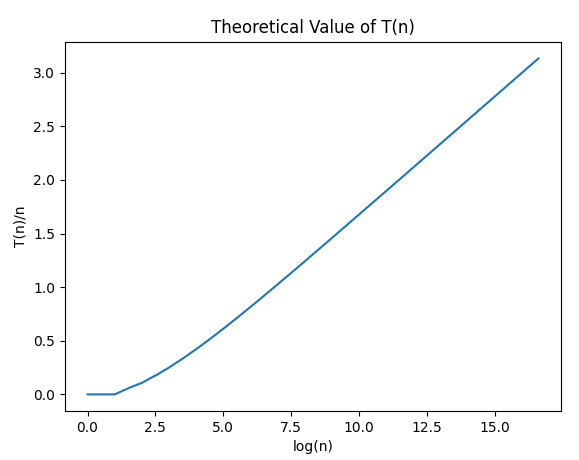
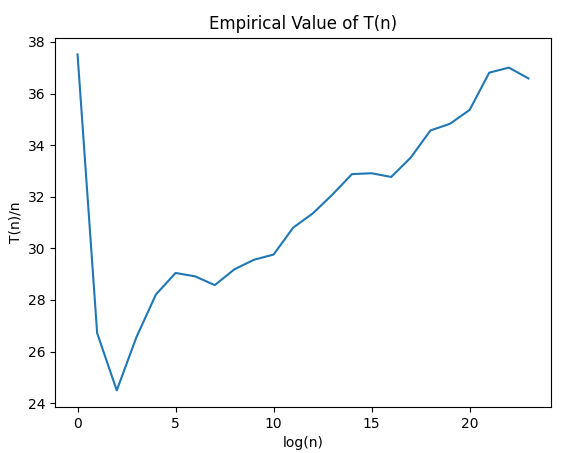
I'm using a Ryzen 7 3700X CPU with the compile command g++ xxx.cpp -O2.
References
[1] https://en.wikipedia.org/wiki/Catalan_number
[2] https://www2.math.upenn.edu/~wilf/gfologyLinked2.pdf
[3] https://www.sciencedirect.com/science/article/pii/S0195669813800534
[4] https://uoj.ac/problem/273
[5] http://www.cs.otago.ac.nz/staffpriv/mike/Papers/RandomGeneration/RandomBinaryTrees.pdf
[6] https://codeforces.me/blog/entry/45723
[7] https://codeforces.me/blog/entry/18291
[8] https://codeforces.me/blog/entry/87585











Some noteworthy recent problems where such a generator was used are as follows:
It was only in the end when I realized that "generating" in "generating balanced sequences" was not an adjective, as in "generating functions"
))()((
is not irreducible. or am i wrong somewhere.
sorry, got it.