Привет, codeforces!
Сегодня, ориентируясь на статью Триангуляция полигонов с сайта neerc.ifmo.ru, я реализовал триангуляцию любых многоугольников без самопересечений (в том числе не являющихся выпуклыми) на C++.
$$$\text{ }$$$
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
Привет, codeforces!
Сегодня, ориентируясь на статью Триангуляция полигонов с сайта neerc.ifmo.ru, я реализовал триангуляцию любых многоугольников без самопересечений (в том числе не являющихся выпуклыми) на C++.
$$$\text{ }$$$
Hello, codeforces!
Do you have modern GPU and CPU and want to calculate something with them, but you don't know how to do it? Dont be upset, because you can read this blog and run your first GPU program on your AMD/Intel/NVIDIA GPU. I will describe an installation process and then we will dive into the C++ code. As an example, we will calculate a lot of mazes for Bug Game in parallel. For doing this in simple way, we will use library Boost.Compute, which is a C++ STL-style wrapper over OpenCL library.
Привет Codeforces!
UPD. I_love_natalia сломал чекер своим лабиринтом на $$$10^9$$$ ходов. Проблема сейчас решена и все решения перетестированы. Система оценивания изменена. Подробнее
UPD 2: Официальный сайт https://buglab.ru/ был обновлен. Обратите внимание на комментарий.
UPD 3: Чекер был ускорен mfv в $$$2.2$$$ раза (по сравнению с моей версией, бенчмарк: $$$4$$$ секунды на $$$1$$$ млрд шагов на вкладке "Запуск"). Текущие рекордсмены:
UPD 4: Я обновил чекер: теперь поддерживаются лабиринты вплоть до $$$42$$$ миллиардов шагов до того, как чекер получит вердикт TLE. Лимит на время выполнения чекера на codeforces равен $$$1$$$ минуте. Я отправил лабиринт с числом шагов равным $$$42.015.084.960$$$ и ответ был вычислен за 59799 мс. Может кто-нибудь может посчитать ответ быстрее?
Я с радостью приглашаю вас принять участие в неофициальном зеркале игры «Жук». В этой игре от вас требуется сгенерировать $$$21 \times 31$$$ лабиринт с максимальным количеством ходов жука до выхода из него. Жук перемещается не оптимально и вы сможете увидеть описание алгоритма его перемещения в условии задачи. Основываясь на данном алгоритме, вы сможете создать свой лабиринт и отправить его!
Приватность: ваши решения (ваши лабиринты) будут видны только mfv.
Ссылка-приглашение: нажми сюда
Дата начала: 18 апреля, 2023, 00:00 MSK
Длительность: 2 недели, а затем дорешивание и виртуальное участие.
Система оценивания: если сгенерированный вами лабиринт заставит жука сделать $$$X$$$ ходов до выхода, то ваше решение получит $$$\frac{x}{10^5}$$$ очков.
Официальный сайт игры: нажми сюда

В 2004 году на просторах интернета появилась игра "Жук", рекламный блог на CF, где необходимо построить лабиринт, который задержит Жука на как можно более длительное время. Сегодня я обновил свой рекорд, построив лабиринт на $$$93.401.998$$$ ходов и, заняв 6-е место в топе, решил сделать зеркало этой игры, подготовив задачу на платформе Polygon и добавив в мэшап на codeforces. У меня это получилось, можно сабмитить решения и набирать баллы, но получилось не так, как хотелось бы... Буду рад, если кто-нибудь подскажет, как решить возникшие проблемы.
Всем привет!
Допустим, два раза в год проводятся внутренние соревнования вуза по олимпиадному программированию в формате Div3 контеста: новогодний чемпионат в конце первого семестра (в декабре) и летний чемпионат в конце второго семестра (в мае), оба перед сессией.
Какие есть идеи о том, какое финансирование у руководства вуза нормально попросить на награждение призёров и что дарить призёрам? Какие можно придумать номинации? Я имею в виду, что не только занял первые K мест, а что-то вроде «за первый сабмит по самой сложной задаче» или «самое короткое/быстрое/оригинальное решение»?
Футболка с распечатанным Деревом Фенвика или бинарным поиском на чёрном фоне плохо смотрится: код не видно на теле, особенно не у плоских людей, да и размеры футболок призёров заранее не угадаешь. Блокноты с крутым олимпиадным принтом бесполезны: никто не пользуется блокнотами, все пишут на первых попавшихся листах А4, затем выбрасывают в урну или на пол. Остаются только книги, но какие? Олимпиадное программирование Лааксонена уже есть у многих первокурсников, а Окулов уже не издаётся.
Что можете посоветовать?
Всем привет!
PBDS настолько гибкая, что мы можем использовать свои структуры node_update с __gnu_pbds::tree<...> (tree из набора policy-based data structures). В качестве примера, можно использовать interval_node_update_policy, чтобы построить Дерево Интервалов как у Кормена. Это описано здесь.
Как вы, возможно, уже знаете: tree_order_statistics_node_update, которую все используют по дефолту, хранит размер поддерева в каждой ноде. Вместо этого нам никто не мешает хранить сумму в поддереве для вычисления суммы элементов множества на отрезке за $$$O(\log{n})$$$. Итак, эта сумма на отрезке [L,R] равна set.order_of_key(R+1)-set.order_of_key(L).
Всем привет!
Я взял всем известный ordered_set в C++ (а точнее __gnu_pbds::tree<...> из GNU C++ Standard Template Library с реализованными Policy-Based Data Structures), унаследовался от него и добавил новые методы к наследнику:
lower_bound_with_order -> возвращает итератор на минимальный >= элемент + его индекс в множестве (порядок);
upper_bound_with_order -> возвращает итератор на минимальный > элемент + его индекс в множестве (порядок);
count_less -> количество элементов, меньших заданного;
count_less_equal -> количество элементов, меньших либо равных заданному;
count_greater -> количество элементов, больших заданного;
count_equal -> просто количество равных элементов.
Преимущество (1) и (2) в том, что это всё считается за один обход дерева (один логарифм). Если вызывать сначала lower_bound, а затем для него order_of_key, то будет два обхода дерева — два логарифма.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
template<typename T, typename Comp = std::less<T>>
using OrdTreeBase = __gnu_pbds::tree<T, __gnu_pbds::null_type, Comp,
__gnu_pbds::rb_tree_tag,
__gnu_pbds::tree_order_statistics_node_update>;
template<typename T, typename Comp = std::less<T>>
struct OrderedSet : public OrdTreeBase<T, Comp>
{
using Base = OrdTreeBase<T, Comp>;
OrderedSet(const auto &...pack)
: Base(pack...) { }
size_t count_less(const auto &key) const {
return this->order_of_key(key);
}
size_t count_less_equal(const auto &key) const {
return upper_bound_with_order(key).second;
}
size_t count_greater(const auto &key) const {
return this->size() - count_less_equal(key);
}
size_t count_equal(const auto &key) const {
return count_less_equal(key) - count_less(key);
}
template<typename Compare = Comp>
std::pair<typename Base::const_iterator, size_t>
lower_bound_with_order(const auto &key) const
{
auto prev = this->m_p_head;
auto curr = this->m_p_head->m_p_parent;
size_t order{};
while (curr != 0)
if (Compare()(curr->m_value, key)) {
order += curr->m_metadata;
if ((curr = curr->m_p_right))
order -= curr->m_metadata;
} else {
prev = curr;
curr = curr->m_p_left;
}
return std::make_pair(prev, order);
}
template<typename Compare = Comp>
std::pair<typename Base::const_iterator, size_t>
upper_bound_with_order(const auto &key) const
{
auto prev = this->m_p_head;
auto curr = this->m_p_head->m_p_parent;
size_t order{};
while (curr != 0)
if (Compare()(key, curr->m_value)) {
prev = curr;
curr = curr->m_p_left;
} else {
order += curr->m_metadata;
if ((curr = curr->m_p_right))
order -= curr->m_metadata;
}
return std::make_pair(prev, order);
}
};
const int INF = (int)1e9+7;
template<typename T, typename Comp>
void test(const char * name) {
printf("--------------------------------------\n");
printf("test: %s\n", name);
std::vector<T> vec;
for (int i = 0; i < 10; i += 2)
vec.push_back(i);
OrderedSet<T, Comp> set(vec.begin(), vec.end());
printf("set:");
for (auto it : set)
printf(" %d", it);
printf("\n");
printf("lower_bound_with_order:\n");
for (int i = -1; i < 10; i++) {
auto [it, order] = set.lower_bound_with_order(i);
if (it != set.end())
assert(set.order_of_key(*it) == order);
else
assert(order == set.size());
int value = (it == set.end()) ? INF : *it;
printf("\t%d: lb = %d, order = %lu\n", i, value, order);
}
printf("upper_bound_with_order:\n");
for (int i = -1; i < 10; i++) {
auto [it, order] = set.upper_bound_with_order(i);
if (it != set.end())
assert(set.order_of_key(*it) == order);
else
assert(order == set.size());
int value = (it == set.end()) ? INF : *it;
printf("\t%d: up = %d, order = %lu\n", i, value, order);
}
}
int main() {
test<int, std::less<int>>("test sorted");
test<int, std::greater<int>>("test reversed");
}
test: test sorted
set: 0 2 4 6 8
lower_bound_with_order:
-1: lb = 0, order = 0
0: lb = 0, order = 0
1: lb = 2, order = 1
2: lb = 2, order = 1
3: lb = 4, order = 2
4: lb = 4, order = 2
5: lb = 6, order = 3
6: lb = 6, order = 3
7: lb = 8, order = 4
8: lb = 8, order = 4
9: lb = 1000000007, order = 5
upper_bound_with_order:
-1: up = 0, order = 0
0: up = 2, order = 1
1: up = 2, order = 1
2: up = 4, order = 2
3: up = 4, order = 2
4: up = 6, order = 3
5: up = 6, order = 3
6: up = 8, order = 4
7: up = 8, order = 4
8: up = 1000000007, order = 5
9: up = 1000000007, order = 5
test: test reversed
set: 8 6 4 2 0
lower_bound_with_order:
-1: lb = 1000000007, order = 5
0: lb = 0, order = 4
1: lb = 0, order = 4
2: lb = 2, order = 3
3: lb = 2, order = 3
4: lb = 4, order = 2
5: lb = 4, order = 2
6: lb = 6, order = 1
7: lb = 6, order = 1
8: lb = 8, order = 0
9: lb = 8, order = 0
upper_bound_with_order:
-1: up = 1000000007, order = 5
0: up = 1000000007, order = 5
1: up = 0, order = 4
2: up = 0, order = 4
3: up = 2, order = 3
4: up = 2, order = 3
5: up = 4, order = 2
6: up = 4, order = 2
7: up = 6, order = 1
8: up = 6, order = 1
9: up = 8, order = 0
Забирайте себе, если нужно. На очереди допиливание для ordered_multiset. Пробую ordered_set с компаратором std::less_equal вместо std::less...
Всем привет! Хочу показать вам реальный пример, в котором использование следующих плюшек ускорения ввода-вывода:
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
приводит к замедлению программы, написанной на C++, в два раза!
Пример довольно простой — мы будем выводить в двоичном представлении все целые числа из отрезка $$$[0,10^7)$$$:
#include <bits/stdc++.h>
using namespace std;
int main() {
//ios::sync_with_stdio(false);
//cin.tie(0); cout.tie(0);
char buf[33]={0};
buf[32] = '\n';
for (int i = 0; i < 10'000'000; i++) {
for (int bit = 30; bit >= 0; bit--) {
buf[30-bit] = ((i >> bit) & 1) ? '1' : '0';
}
cout << buf;
}
}
UPD. Когда я заменил buf[32] = '\n'; на buf[31] = '\n';, чтобы последним символом был '\0', а предпоследним — '\n', ситуация кардинально не изменилась.
Если мы запустим этот пример в codeforces custom invocation, то мы увидим Used: 1840 ms, 1184 KB. Когда мы раскоментируем закоментированные строки, ускоряющие ввод-вывод в C++, мы увидим Used: 3759 ms, 1188 KB. Это ловушка!
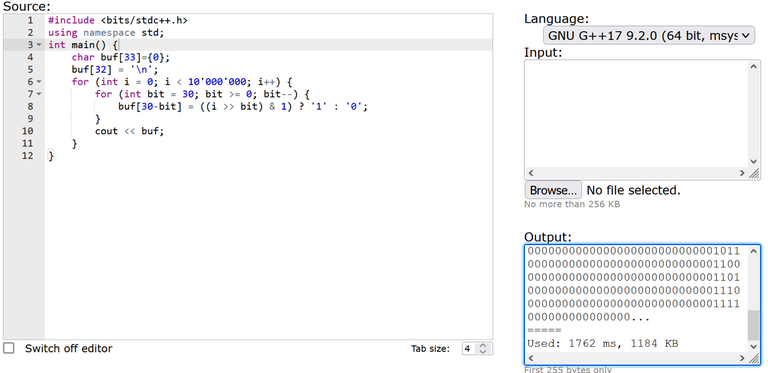
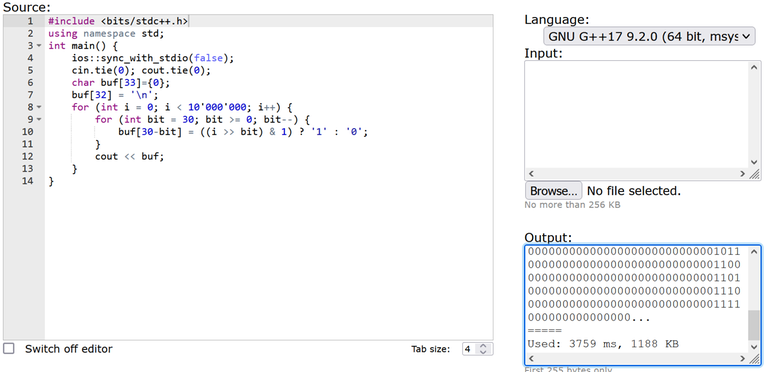
UPD2. AsGreyWolf предложил использовать компилятор GNU G++20 11.2.0 (64 bit, winlibs) вместо GNU G++17 9.2.0 (64 bit, msys 2) и это решило проблему замедления. Для любого другого GNU компилятора, доступного на codeforces, проблема сохраняется.
Hello, codeforces!
Everyone knows that operation a * b % mod is not calling div and mod assembler commands. Instead of it only integer multiplication (imul) and bit shift in right (sar) are used: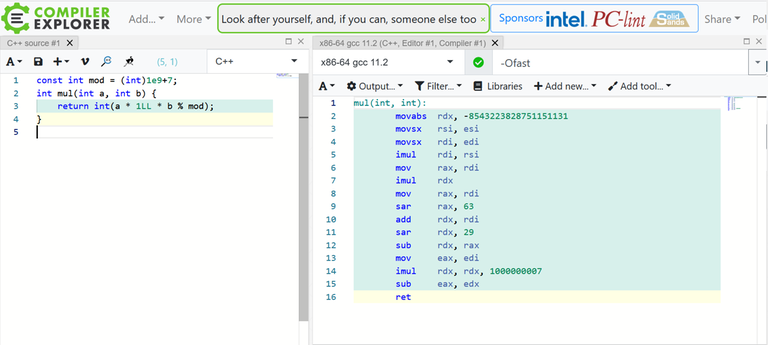
I remember from comments for one of the editorials on the codeforces that Intel and AMD have a special extended ASM command for it, that can calculate even faster for assumption that a and b are 32-bit integers and mod is constant that is known at compilation time.
Today I can't find this command, this editorial and this comment from red coder with his template where this command is used for modulo multiplication. Maybe someone knows this ASM command and can help with it?
Всем привет!
Надеюсь, что вы моете руки и чувствуете себя хорошо.
В условиях карантина и каникул, конечно же, можно заниматься активной умственной деятельностью и решать интересные задачки, но задачки есть не только по программированию, но и по математике!
Напоминаем Вам, что, традиционно, в ЮУрГУ проходят дистанционные конкурсы по математике. Каждый конкурс состоит из 5-6 задач, на решение которых отводится месяц или даже больше. На текущий момент, идут сразу два конкурса:
Это означает не только то, что Вы можете принять участие в этих конкурсах, а еще и то, что уже сейчас доступны целых 67 конкурсов с интересными задачами по математике и их разборами, с помощью которых Вы можете прокачать свои знания математики.
Ссылка на пост в VK, содержащий условия задач конкурсов №68 и №69 в формате pdf. В этой же группе Вы можете найти и 67 предыдущих конкурсов.
Удачи! Прошу воздержаться от обсуждения задач до окончания конкурса.
P.S. Призы предусмотрены только для участников из Челябинска
В данном блоге приводится эффективная реализация умножения Карацубы двух многочленов.
Чтобы найти ошибку в коде нужно просто...
Hi! I created mashup, added mashup to private group as a contest (6 hours ago). In this group one user is the group manager (joined as a manager 6 hours ago). Why I can't set him as a contest manager? Error message: user is not a gym manager. Tried 20-30 times with different time interval.
Hello everybody!
If you want to use binary search over array with known at compile time size, and this size can be extended to power of two, you can use next simple template:
template<int n, typename T>
int lowerBound(const T* __restrict arr, const T val) {
if (n == 1) { return val > arr[0]; }
else {
constexpr int mid = n / 2;
if (val > arr[mid]) { return mid+lowerBound<n-mid, T>(arr+mid, val); }
else { return lowerBound<mid, T>(arr,val); }
}
};
Testing on ideone shows, that it is faster in 4 times in comparison with std::lower_bound.
Thanks for reading this.
UPD. Testing for doubles, in 3.5 times faster.
Hi, I cant understand, why my solution to problem 1137C. Museums Tour is getting WA79. Testcase is large, I tried to found by brute force on small graphs for n <= 4 and d <= 4 and compare with other accepted solutions and did not found counter-test. Can anybody help with understanding why my solution got WA79?
UPD. Fixed. Looks like we can't use dynamic programming on topological order, where we will update dp like: dp[next] = std::max(dp[next], dp[curr] + value[next]) for all edges curr->next, we only allowed use dynamic programming like dp[curr] = std::max(dp[curr], dp[prev]+value[curr]) for all edges prev->curr. Accepted try, difference with wa79.
UPD. Оригинал статьи оказался доступен в кэше поисковой системы mail.ru, спасибо r3t. запрос, результат
Всем привет! Сегодня обнаружил, что старая статья про остатки от деления на 2p - 1 недоступна больше по этому адресу, ее нет ни в кэше яндекса, ни в кэше гугла. В ней описывались и доказывались интересные факты о вычислении остатков от делений на числа вида 2p - 1, а также было указано как и где они применялись. Если эта статья доступна на каком-то другом ресурсе, или вы знаете аналогичную статью, то прошу поделиться в комментариях. Ниже я кратко перескажу то, что помню, чтобы информация не потерялась, вдруг никто не найдет.
Для начала рассмотрим систему счисления по основанию 10 и остатки от деления на 9. Известен признак делимости на 9: число делится на 9, если сумма его цифр делится на 9. Например, число 936 делится на 9, так как сумма его цифр 9 + 3 + 6 = 18 делится на 9. Действительно, 936 = 104·9. Этот признак делимости следует из представления числа в десятичной системе счисления:

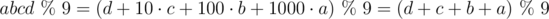
В общем случае, если число представлено в системе счисления по основанию b, то для взятия остатка от деления на b - 1 можно взять остаток от суммы его цифр, так как для любого p верно: 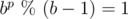 .
.
Так как в компьютерах используется двоичная система счисления, то мы можем только при помощи битовых операций брать остатки от деления на числа вида 2p - 1, представляя числа в системе счисления по основанию 2p. Это применяется, например, в вычислении полиномиального хеша от строк по модулям 231 - 1 и 261 - 1 — простым числам Мерсенна.
Стоит заметить, что если осуществлять только переход от числа к сумме его цифр, то мы будем получать смещенный остаток, то есть число из диапазона [1, 2p - 1]? Чтобы этого избежать, необходимо на какой-либо итерации прибавить 1, а в конце из результата вычесть 1, чтобы сместить весь диапазон получаемых остатков от деления из [1, 2p - 1] в [0, 2p - 2].
Прибавим к числу 1, получим 1241432, сумма цифр 1 + 2 + 4 + 1 + 4 + 3 + 2 = 17. Сумма цифр полученного числа 1 + 7 = 8, получили число из диапазона [1, 9], вычитая 1, получаем настоящий остаток от деления, равный 7.
Прибавляя 1, получим 999999999 + 1 = 1000000000, сумма цифр равна 1, вычтем 1 и получим 0 — остаток от деления.
Прибавляя единицу, получаем: 231, представляя в системе счисления по основанию 216, получаем 215·216. Сумма цифр равна 215, было получено число из диапазона [1, 216 - 1], вычитая 1, получаем остаток от деления, равный 215 - 1.
Интересный вопрос: сколько раз нужно перейти от числа к его сумме для вычисления остатка от деления? Если мы представим число n в системе счисления по основанию b, то после взятия суммы его цифр, мы получим число, порядка 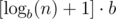 , то есть, чисто интуитивно, таких редукций нужно сделать немного.
, то есть, чисто интуитивно, таких редукций нужно сделать немного.
К счастью, нам не нужно считать это для каких-то абстрактных чисел n и b, посчитаем лучше, сколько нужно редукций, чтобы взять остаток от деления 64-битного числа по модулю 231 - 1. Для этого нужно представить число в системе счисления по основанию 231, получим: a + 231·b + 262·c. Знаем, что a + b < = 2·(231 - 1), c < = 3, получаем a + b + c < = 232 + 1 < = 231·2 + 1. Нам точно понадобится еще одна редукция, и тогда худшим случаем будет, когда сумма цифр данной суммы снова превысит 231 - 1, и нам нужно будет сделать последнюю редукцию, получаем, что 3 — достаточно.
В качестве дополнения, ниже приведены реализации операций сложения, вычитания и умножения по модулю 261 - 1, использующиеся в полиномиальном хеше.
typedef unsigned long long ull;
const ull MOD = (ull(1) << 61) - 1;
ull reduction(const ull a) {
// Given 0 <= a < 2^64. Need to get sum of digits in base 2^61.
return (a & MOD) + (a >> 61);
}
ull mod(const ull a) {
// Given 0 <= a < 2^64. Need to calculate a % MOD
return reduction(reduction(a)+1)-1;
}
ull add(ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a + b) % MOD
return (a += b) >= MOD ? (a -= MOD) : a;
}
ull sub(ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a - b) % MOD
return (a -= b) >= MOD ? (a += MOD) : a;
}
ull mul(const ull a, const ull b) {
// Given 0 <= a, b < mod. Need to calculate (a * b) % MOD
// a = a0 + a1 * 2^32
// b = b0 + b1 * 2^32
// a * b = a0 * b0 + (a0 * b1 + a1 * b0) * 2^32 + a1 * b1 * 2^64
const ull a0 = a & ~0u, a1 = a >> 32;
const ull b0 = b & ~0u, b1 = b >> 32;
const ull mid = a0 * b1 + a1 * b0;
return mod(reduction(a0 * b0) + (a1 * b1 << 3) + (mid >> 29) + (mid << 32 & MOD));
}
UPD. Все, что будет описано ниже, давным давно делает tourist, например, в последней своей посылке.
В древних задачах на сайтах acmp, e-olymp и timus часто ограничения по памяти крайне малы и равны 16 МБ, 32 МБ, 64 МБ. Скорее всего, для современных ограничений в 256 МБ и 512 МБ описанный ниже способ достижения минимального потребления памяти под дерево отрезков не актуален, но все же рассмотрим способ, позволяющий его достичь в реализации сверху-вниз. Будем использовать ровно 2·n - 1 узлов, а вершины пронумеруем в порядке эйлерова обхода:
0
1 8
2 5 9 10
3 4 6 7
Тогда, если мы находимся в узле v и это не лист, то у него есть левое и правое поддеревья. Номер левого поддерева равен v + 1, так как в порядке эйлерова обхода мы посетим его сразу после текущего узла. Что касается правого поддерева, то туда мы пойдем только когда посетим корень и все вершины левого поддерева. Количество вершин в поддереве зависит только от длины отрезка, соответствующего узлу дерева.
Будем считать, что если у нас есть отрезок [l, r], то левому поддереву соответствует отрезок [l, m], а правому — [m + 1, r], где m = (l + r) / 2. Тогда длина левого отрезка будет равна m - l + 1, а количество узлов в нем 2·(m - l + 1) - 1.
Окончательно получаем, что для узла v, соответствующего отрезку [l, r], левое поддерево в нумерации в порядке эйлерова обхода будет иметь номер v + 1, а правое — номер v + 2·(m - l + 1), где m = (l + r) / 2 — середина отрезка [l, r].
Hi! Maybe someone wants to realize crazy ideas using uint128_t during contest. I implemented some functionality (<<,>>,-,+,*,%,/) and tested on problem 984C. Finite or not?. If there are any bugs or optimizations which can reduce runtime, please tell.
Недавно узнал, что многие двумерные задачи на offline запросы можно решить с помощью сканирующей прямой и дерева отрезков или дерева фенвика, но не могу найти, на чем потренироваться. Надеюсь, вы можете подкинуть куда можно эту штуку заслать. Заранее спасибо!
Хочу предостеречь особо пытливых — не стоит искать в интернете секретный архив tourist codeforces. Ниже привожу комментарии людей, которые вчера днем успели налететь на него, но на codeforces я их не нашел. Похоже, что это все боты, а на сайте работают мошенники, которые после ввода номера телефона списывают со счета деньги! Ссылку не даю ради вашей же безопасности.








Проблема: один и тот же код, отправленный 5 раз с различными комментариями в тексте кода получает различный вердикт от проверяющей системы codeforces: от accepted до tle. Ссылка на оригинальное изображение.

Первая группа одинаковых решений: 42063540, 42063549, 42063558, 42063574, 42063583
Вторая группа одинаковых решений: 42063251, 42063390, 42063403, 42063414, 42063421
Вы можете сравнить код и убедиться, что он в каждой группе совпадает, я напуган и не знаю возможно ли, что мое правильное решение получит неправильный вердикт во время соревнования?
Как вы думаете, опасно ли оставлять комментарии в коде решения? Читает ли проверяющая система их и замедляет ли это ее работу?
UPD: Это шестая посылка из первой группы одинаковых решений с временем 3088 ms
Понимание того, как простым конструктивом построить гамильтонов цикл в строго связном турнире, основываясь на его свойствах, было критично на региональном этапе всероссийской олимпиады школьников по информатике в сезоне 2014/2015 для получения полного балла по задаче Магические порталы.
здесь разборы от Меньшикова Федора Владимировича: часть 1, часть 2, часть 3. В разборах представлен более сложный алгоритм построения гамильтонова цикла.
На acmp.ru также нужна помощь от инициативных людей с переводом условий задач с русского на английский, так как в тестовом режиме вводится английский язык. Некоторые задачи уже переведены (порядка сотни), можно вбивать locale=en в адресную строку. Желающим помочь можно писать либо Беляеву Сергею Николаевичу [email protected], либо Меньшикову Федору Владимировичу [email protected].
Пусть дан ориентированный граф, в котором между любыми двумя вершинами есть направленная дуга, а также для любой пары вершин u и v можно дойти из u в v по ориентированным дугам, а затем успешно вернуться также по ориентированным дугам обратно ( строго связный турнир ). Пример такого графа:
В таком графе есть гамильтонов путь — путь, проходящий по всем вершинам (например:  ), и гамильтонов цикл — гамильтонов путь, в котором из конца есть дуга в начало (например:
), и гамильтонов цикл — гамильтонов путь, в котором из конца есть дуга в начало (например: 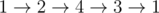 ). Рассмотрим алгоритм нахождения и того, и того за O(n2).
). Рассмотрим алгоритм нахождения и того, и того за O(n2).
Удобнее всего строить по индукции. Пусть уже есть путь 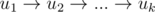 из k вершин. Надо добавить к нему новую вершину uk + 1. Делаем следующее:
из k вершин. Надо добавить к нему новую вершину uk + 1. Делаем следующее:
Находим максимальный номер i такой, что из любой вершины u1, u2, ..., ui ведет ребро в uk + 1.
Вставляем новую вершину после ui, получая путь: 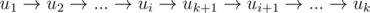
Здесь активно используется тот факт, что граф у нас — строго связный турнир, а это значит, что если из u в v нет дуги, то точно есть дуга из v в u.
Начиная с пустого пути, добавляем в него все вершины по очереди, каждая операция вставки требует O(n) действий, всего нужно вставить n вершин, следовательно, спустя O(n2) действий получим гамильтонов путь.
Можно сделать это за 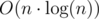 — подробнее в прикрепленных источниках.
— подробнее в прикрепленных источниках.
Стратегия следующая: раз мы уже умеем находить гамильтонов путь, то сперва найдем его за O(n2), а затем уже преобразуем в гамильтонов цикл за O(n2) действий (можно сделать это за O(n) — подробнее в прикрепленных источниках).
После нахождения гамильтонова пути 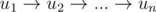 необходимо перестроить его в цикл, обеспечив наличие ребра из последней вершины цикла в первую. Сделаем небольшие приготовления:
необходимо перестроить его в цикл, обеспечив наличие ребра из последней вершины цикла в первую. Сделаем небольшие приготовления:
Пойдем по всем вершинам пути u3, u4, ..., uk до тех пор, пока есть ребро из uk в u1. Если дошли до конца пути, то цикл найден — это весь путь, иначе есть некий цикл  и остаток пути
и остаток пути 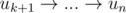 . Далее будем по индукции расширять цикл, добавляя вершины из пути. Рассмотрим два случая:
. Далее будем по индукции расширять цикл, добавляя вершины из пути. Рассмотрим два случая:
Если в цикле есть вершина, в которую идет ребро из добавляемой вершины uk + 1, то находим первую такую вершину ui. Теперь мы можем составить новый цикл 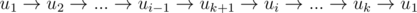 , а путь будет выглядеть как
, а путь будет выглядеть как  .
.
Если в цикле не нашлось вершины, в которую бы шло ребро из добавляемой вершины uk + 1, пройдем по остальным вершинам пути, пока не найдем вершину uj, для которой такая вершина ui все же найдется (такая вершина должна быть, иначе этот граф не строго связный турнир, так как мы нашли способ его разбиения на две компоненты строгой связности). Тогда все вершины из начала пути до uj добавляем в цикл, перестраивая его следующим образом: 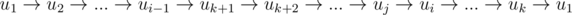 . От пути либо ничего не остается, либо остается
. От пути либо ничего не остается, либо остается  .
.
На каждой итерации мы увеличиваем длину цикла как минимум на 1, выполняя при этом O(n) операций. Итоговая асимптотика алгоритма O(n2).
В приведенных источниках есть способ нахождения гамильтонова пути и цикла за 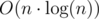 со структурой данных Semi-Heap, который можно применять на строго связных турнирах, состоящих из порядка 200.000 вершин, а направление ребер в которых определяется некоторой функцией f(u, v) от номеров вершин:
со структурой данных Semi-Heap, который можно применять на строго связных турнирах, состоящих из порядка 200.000 вершин, а направление ребер в которых определяется некоторой функцией f(u, v) от номеров вершин:
Здравствуйте!
Написано ли в правилах codeforces что-то вроде "не создавать обсуждений задач в еще не завершенных контестах"? Здесь довольно часто появляются посты с темой "помогите решить задачу", причем авторы этих постов иногда не дают никакой информации о том, откуда эта задача, какие идеи они пробовали, что получилось / не получилось, это настораживает...
Вот пример такого поста: в комментариях уже можно найти исходный код предоставленного его автору решения. Кто знает, может быть эта задача с какого-нибудь зарубежного соревнования вроде нашего SnarkNews summer series, раунды которого длятся чуть больше недели.
Какие у вас мысли на этот счет и что можно предпринять против тех, кто, возможно, хочет выехать за счет доброты других?
Здравствуйте! Есть задача на acmp и решение в вещественных числах с использованием типа double.
Дан радиус окружности и даны прямые, заданные двумя точками, точки могут лежать как внутри круга, так и на окружности, требуется проверить для каждой пары прямых, лежит ли точка пересечения внутри круга, на нем или снаружи. Во входных данных все числа вещественные и могут быть заданы с 6-тью знаками после запятой, их абсолютные величины не превосходят 100, то есть, нужно 8 разрядов для точного представления.
В ходе решения при пересечении прямых возникают числа, в которых 16 разрядов, а также происходит их деление, в связи с этим есть ощущение, что точности типа double не хватает. Судя по всему, контр-тест должен содержать ровно две прямые, которые пересекаются очень близко к окружности, или пересекаются прямо на окружности. Я попробовал построить пересечение в точке (99.999999, 0.014142) с радиусом 100, тогда разность радиус-вектора точки и радиуса окружности будет порядка 3.835·10 - 9, с чем благополучно справляется тип double.
Есть две посылки на C#: с многопоточкой — Accepted и без многопоточки — TLE. Автор решения использует Parallel.For в функции MultiplyMatrixPow, за счет чего и добивается успеха. Вопрос: сколько ядер мы можем нагружать на серверах codeforces при проверке нашего решения?
UPD: Многопоточка здесь ни при чем. В первом решении автор берет остаток от деления три раза, во втором всего один. Отсюда и выигрыш.
| Название |
|---|


