Motivation & Problem
Recently saw this problem. For some this problem might seem like a segment tree problem and it is indeed one. However this problem and others where segment tree does not apply can be solved using another approach. I will rephrase the problem in a simpler way. We want a data structure capable of doing three main update-operations and some sort of query. The three modify operations are:
add: Add an element to the set.
remove: Remove an element from the set.
updateAll: This one normally changes in this case subtract X from ALL the elements. For this technique it is completely required that the update is done to ALL the values in the set equally.
And also for this problem in particular we may need one query:
getMin: Give me the smallest number in the set.
Observing this operations we want to handle, SegmentTree seems legit except for the remove, but we can wave it around by assigning INF to the position we want to remove. However if we don't have the updateAll then we can just use a MULTISET. And in fact if the remove is only to the minimum element then we can use a HEAP. However the four operations without any "workaround" can only be managed by a DynamicSegmentTree which in fact exists but is like using a bazooka to kill a simple mosquito.
Interface of the Data Structure
struct VeniceSet {
void add(int);
void remove(int);
void updateAll(int);
int getMin(); // custom for this problem
int size();
};
Usage of this methods
So imaging we have this four operations, how can we tackle this problem with it. Well i will illustrate it with a simple code in C++ which i hope is self explanatory.
VeniceSet mySet;
for (int i = 0; i < N; ++i) {
mySet.add(V[i]);
mySet.updateAll(T[i]); // decrease all by T[i]
int total = T[i] * mySet.size(); // we subtracted T[i] from all elements
// in fact some elements were already less than T[i]. So we probbaly are counting
// more than what we really subtracted. So we look for all those elements
while (mySet.getMin() < 0) {
// get the negative number which we really did not subtracted T[i]
int toLow = mySet.getMin();
// remove from total the amount we over counted
total -= abs(toLow);
// remove it from the set since I will never be able to substract from it again
mySet.remove(toLow);
}
cout << total << endl;
}
cout << endl;
Implementation of the Technique
As the title says I don't call it a data structure itself but this is a technique almost always backed up by a data structure. And now I am going to explain why I call it Venice technique. Imagine you have an empty land and the government can make queries of the following type: * Make a building with A floors. * Remove a building with B floors. * Remove C floors from all the buildings. (A lot of buildings can be vanished) * Which is the smallest standing building. (Obviously buildings which are already banished don't count)
The operations 1,2 and 4 seems very easy with a set, but the 3 is very cost effective probably O(N) so you might need a lot of workers. But what if instead of removing C floors we just fill the streets with enough water (as in venice) to cover up the first C floors of all the buildings :O. Well that seems like cheating but at least those floor are now vanished :). So in order to do that we apart from the SET we can maintain a global variable which is the water level. so in fact if we have an element and want to know the number of floors it has we can just do height - water_level and in fact after water level is for example 80. If we want to make a building of 3 floors we must make it of 83 floors so that it can tough the land. So the implementation of this technique might look like this.
struct VeniceSet {
multiset<int> S;
int water_level = 0;
void add(int v) {
S.insert(v + water_level);
}
void remove(int v) {
S.erase(S.find(v + water_level));
}
void updateAll(int v) {
water_level += v;
}
int getMin() {
return *S.begin() - water_level;
}
int size() {
return S.size();
}
};
Variations
Trick With Trie
Probably you have seen a problem of having a set of numbers and handle queries such as what is the greatest XOR than can be achieved by using one number of the set and the given number. This can be handled with a BinaryTrie. However if we add the operation XOR all the numbers in the set this would be very heavy. But if we maintain a global water_level that would XOR any number in and any number out, then it would virtually be XORING all the numbers in the set. Don't have an example problem yet, but I know I have used it, so any is welcome.
So as my experience is, this technique is a lightweight modification that can be applied to all DataStructures that support (add, remove and query) and only need the operation (updateAll).
Other Approaches For This Problem
Binary Search: This is very fast and simple, however is an offline solution. (Not apply for other operations such as sort)
Event Processing: Easy to code and fast but still offline and does not apply for other operations such as XOR.
Dynamic Segment Tree: A little slow in practice, same complexity in theory, and requires heavy code. This is online but requires heavy code. (Dynamic means can insert and delete nodes from the segment tree). Does not apply to other variations of the problem such as XOR.
Implicit Segment Tree: Relativly easy to code, but theoretical complexity of Nlog(MAXVAL) and still requires this technique to work. (Does not apply to other variations such as XOR)
Example Problems
- D. Vitya and Strange Lesson — Using the XOR variation
- BDOI16E — Village Fair — Multiple Venice Sets
per query. When I saw the editorial I saw that it had another interesting approach with an update buffer which solved the problem in 
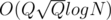, for my surprise my solution was 
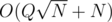summing the creation and queries, and I saw conveniently the author used 
, we create a special node and assign the children to this new node and remove the children from the previous parent.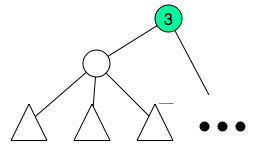 
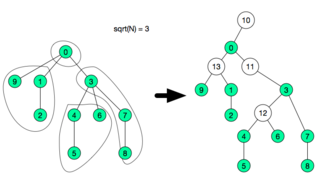
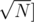if 
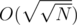or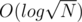 
, although the time constraint will be very tight. 
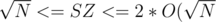since ALL fragments have size 
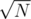then the total number of fragments will be 
