Hello fellow problem-solvers. I am writing this post to ask a doubt I am not able to munch anymore. The problem is Double Sum 3 which came as problem F on Atcoder Beginner Contest 390. I am interested to know the knowledge gaps and thoughts which are preventing me from solving this. I don't just need the solution I want if I ever came across a situation remotely matching this, I am at least able to self realize it if not solve it.

My thoughts:

Given the relation $$$\Sigma_{L=1}^N\Sigma_{R=L}^Nf(L,R)$$$, I was not able to come up with anything linear. So I did what is most obvious to me, created a graph out of the problem. Given the test case, I made a graph:

5

3 1 4 2 4

Now in this, starting from 3, if adding values is taken into a group, its contribution is 0 otherwise it forms a group of its own and its contribution is 1. Each value say arr[i] have an edge to arr[i], arr[i-1] and arr[i+1] because if anyone of these are present then no new component is formed. So this is the final graph: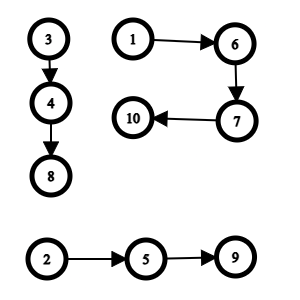

There are 3 disconnected components so the answer for $$$F(1,10)$$$ is 3

The contribution of each index:

$$$[1,1,1,0,0,0,0,0,0,0]$$$

If a node is added and it reduces the number of components like $$$[1,2]$$$ $$$[4,5]$$$ and we add 3 then its contribution is -1 because it reduces our answer.

So now for F(1,3) the answer is 3; F(1,5) the answer is 3 So for $$$\Sigma_{i=1}^NF(i,N)$$$ the answer is the sum of the array contribution across all. For this, across all these are the contributions:

$$$[10,9,8,0,0,0,0,0,0,0]$$$ so the sum of all contributions is 27 and the answer for $$$\Sigma_{i=1}^NF(i,N)$$$ is 27

Now I thought, start from index 1 and start removing the nodes and their contributions and then just sum it as usual. If my sum function is $$$G(start, N)$$$ then I can go from $$$\Sigma_{i=1}^NG(i,N)$$$ so remove the contribution of each index and add it to the sum and I got a net sum the answer.

Removing 1, makes all of its children now to form individual groups and they now contribute +1 more than their usual value. And we can just compute all $$$G(i,N)$$$.

This logic passes all samples and permutation on Atcoder but failed on random tests here.

My code fails for this test case I found after stress-testing:

10

4 1 3 5 2 1 2 5 6 4

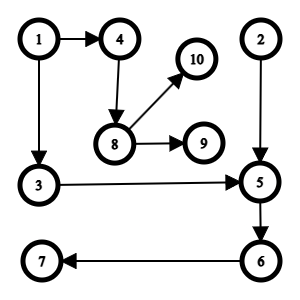
Now why this fails? The contribution of node at index 10 will become -1 after removing node at index 1 because its children are still connected by this index shown in the graph below. Now I can run an algorithm to find if the children as still connected by a bridge vertex find that bridge and decrease its value but this seems too much. What am I missing?

I don't know if this happens to higher rated or more extensive problem-solvers or not but I don't want to keep doing this more than this. I used a DSU and a lot of conditions in code which is readable and good but it seems too complex for a solution.

Hello everyone. I participated in the lowe's coding round and there was this question I was not able to solve completely. I did brute force and passed some test cases though.

The problem says, You are given a connected undirected graph. It has n nodes and m edges. Each node has some sweetness value that will be given to us.

The game is as follows:

1. Alice moves first and she may break a node. Each edge connected to this node will vanish.
2. Bob will pick any connected component(containing all or some nodes)
3. Alice will pick any remaining connected components if there are any

The game ends in three steps. Both of them want to maximize their score by collecting maximum possible sweetness. They are not trying to minimize each other' score.

Determine the maximum score of Alice and Bob respectively. Assume both plays the game optimally.

Graph nodes index starts from 1. If no connected component left, alice gets 0

Input: number of test cases then n, m and then sweetness of each node and then the edges.

Example:

1

6 7

4 3 7 5 9 2

1 2

2 3

1 3

3 4

4 5

5 6

4 6

For this answer is 11 14

I tried to construct a spanning tree and also strongly connected components but couldn't understand.

How to solve this problem? I did this with DFS and max heap. Brute force. What is optimal way of doing this problem

Hello. This is a CSES problem: Sliding Median. My logic is to have a sorted structure which can store multiple keys in sorted order and then I'll take middle of that data structure and then remove by index and do it again. So my time complexity analysis is: O(nlog(n))

I thought of PBDS. Inserting and sorting is find but how to have multiple keys. Using less_equals is not working for me. Is there anything I can do with PBDS or I need to think of some other logic.

My Code with PBDS I have printed the set so to analyze what was going on.

PS: Please don't tell me the logic just help me with the PBDS and this logic otherwise I'll think about something else then :)

Hello everyone. This is a CSES problem: Subarray Distinct Values very simple and straightforward 2 pointer approach. My time complexity is O(n) visiting every array element almost twice. But I am getting TLE. Why.

My code: My Code on CSES

OK so there is this problem of CSES, Stick Lengths

Brief of problem: Given some numbers, you have to make all numbers equal. You can do + or — any number to any number in array and the overall cost is the sum of all the number changes you make. Example, 1 4 10. If we think to make all elements to 5 cost is abs(1-5)+abs(4-5)+abs(10-5). We have to minimize this cost.

Solution: You find the median and compute the answer. This means that you make all elements equal to median. For example in 1 4 10 => it is 4. So minimum answer is: abs(1-4)+abs(4-4)+abs(10-4) = 3+0+6 => 10

What I thought: Let all the numbers be on x axis. Now I want all the points to be at the smallest distance from one central point so that the overall sum should be minimum. Then I thought that this must be mean. Because mean is the middle value of all the elements, converging all the points to mean would be correct. But no it's not mean, it's median.

My Question: Why median works and mean does not. Please give me an easy explanation. A mathematical reasoning which I can build on my way of thinking. Because I am not able to understand why it doesn't work for mean.

Counter example: Let's say we have, 1 2 1005 The mean is = (1+2+1005)/3 => 336. So cost is abs(1-336)+abs(2-336)+abs(1005-336) => 1338 The median is 2. So cost is abs(1-2)+abs(2-2)+abs(1005-2) => 1004 So median works and that is how I basically cheated and solved the question but it doesn't satisfy that inner feeling of why.

PS: Please help and please explain in a light language.