Hi!
There's a problem I'd appreciate some help with (maybe hints or a sketch of solution...)
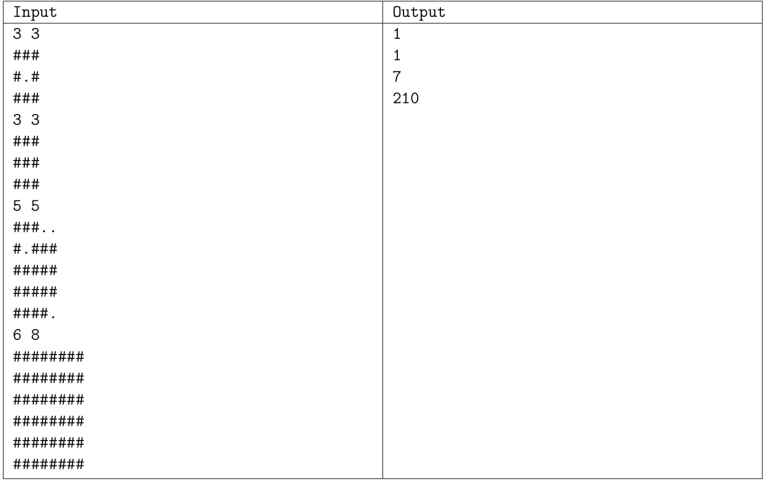
You have an n \times n grid, with n \le 350. Every element of the grid is either '.' or '#'.
The problem asks to count the number of rectangles made of '#', where sides are bigger than or equal to 3.
So the minimal rectangle would be
###
#.#
###
IMPORTANT: There are 100 test cases, so the solution should be around O(N^2 lg N)
I tried to count the complement: As the total number of rectangles in a grid is easy to compute, I tried to focus on every dot and count the number of rectangles it interrupted, but I haven't figured out exactly how to avoid counting things multiple times...