Где-то через неделю пройдет финал VK Cup в Санкт-Петербурге. Вопрос к участникам: получили ли вы хоть какую-то информацию от организаторов (билеты, расписание...)? Мы писали им уже несколько раз на почту и в ВК, но, к сожалению, никакого ответа не получили.
Заранее спасибо за ответ.









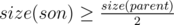 . Заметим, что с вершины вниз может выходить не более одного тяжелого ребра.
. Заметим, что с вершины вниз может выходить не более одного тяжелого ребра.