Кто знает, если я добавил в мешап задачу из полигона, а затем обновил задачу (и её package) в полигоне — какое заклинание произнести, чтобы задача обновилась в мешапе? Или только передобавить можно?
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Подскажите, пожалуйста, возможно ли сейчас создать тренировку, в которой некоторые задачи будут из полигона, а некоторые — с CodeForces? И если да, то как?
В этом посте я хочу рассказать в двух словах о том, как пистать формулы на кодфорсесе так, чтобы они выглядели формулами. По сути это краткое введение в начала языка разметки  , который и используется на Codeforces. Оно будет полезно тем, кто совсем не знает, как писать формулы и почти любому, у кого нет об этом систематических знаний.
, который и используется на Codeforces. Оно будет полезно тем, кто совсем не знает, как писать формулы и почти любому, у кого нет об этом систематических знаний.
Три важных правила
Самое главное правило: формула заключается в доллары ($), как в скобки.
Ещё одно важное правило: если вы хотите, чтобы некоторая операция была применена к целой группе символов, эту группу надо оформить в блок с помощью фигруных скобок. Например, если написать 2^x+y, получится 2x + y. Чтобы получить 2x + y, надо заключить показатель степени в блок: 2^{x+y}
Третье правило — для перфекционистов. Для экономии траффика Codeforces печатает простые формулы, в которых ничего особенного нет, обычным текстом. Иногда это получается не очень красиво C_{x_i+y_i-2}^{x_i-1} = Cxi + yi - 2xi - 1. Если вы напечатали формулу и вам не понравилось, как Codeforces её интерпретировал, можно в начале формулы добавить команду \relax. Тогда формула будет гарантированно красивой, в ущерб траффику: \relax C_{x_i+y_i-2}^{x_i-1} = 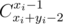 .
.
Арифметические операции.
Сложение и вычитание пишутся обычными знаками + и -. Что касается умножения, то обычно оно в математике обозначается либо просто пустым символом (xy — это произведение чисел x и y). Также есть символ  (
(\cdot). Если же надо перемножить два сложных выражения (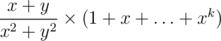 ), или важны оба сомножителя, а не только величина произведения (в выражениях вида поле
), или важны оба сомножителя, а не только величина произведения (в выражениях вида поле  ), используется символ × , который может быть получен командой
), используется символ × , который может быть получен командой \times.
С делением всё несколько сложнее. Обычно в математике деление не пишется в одну строчку, однако желание не городить дроби на ровном месте тоже вполне понятно. В таком случае всегда можно написать : или / (x:y, x/y). Если же вы хотите всё же написать дробь, на это есть две похожие команды: \frac и \dfrac. После любой из этих команд надо написать блок числителя и блок знаменателя, например:  (
(\frac{1}{4}). С использованием \frac дроби получаются маленькие, что подходит, в основном, для самых простых дробей. Если вы хотите написать большую серьёзную дробь, вам потребуется \dfrac: 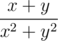 (
(\dfrac{x+y}{x^2+y^2}). В принципе, если числитель или знаменатель односимвольный, можно его не заключать в скобки, например: 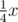 (
(\frac14x), но только если числитель не является буквой.
Верхние и нижние индексы.
Если вы хотите написать нижний индекс, вам поможет символ _, а верхний индекс (в основном это бывает показатель степени), то символ ^: (xi + yi)2 ((x_i+y_i)^2). Так же, как и с дробями, в нижний или верхний индекс можно поместить блок, но если индекс односимвольный, то можно этого не делать.
Разные полезные спецсимволы и советы
Текст — текст (---) — не в формулах, а в тексте. Это тире, а не дефис (не работает, если нет окружающего текста)
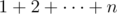 (
(\dots) — среднее многоточие для формул в англоязычных текстах.
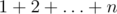 (
(\ldots) — нижнее многоточие для формул в русскоязычных текстах.
∞ (\infty) — символ бесконечности.
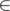 (
(\in) и  (
(\ni) — символы принадлежности к множеству.
→ (\to) — стрелочка направо, в выражениях типа xn → 0.
Многие известные математичские функции можно набирать с \, тогда они будут выглядеть, как формулы, а не просто как текст (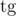 =
= \tg, 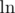 =
= \ln, 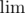 =
= \lim и так далее)
Если вы хотите, чтобы индексы были сверхи и снизу, а не сверху-справа и снизу-справа, используйте команду \limits:
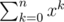 =
= \sum_{k = 0}^nx^k
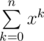 =
= \sum\limits_{k = 0}^nx^k.
Если вокруг большого выражения маленькие скобки, можно их сделать подходящего размера, написав перед левой скобочкой команду \left, а перед правой — команду \right. Например: 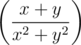 =
= \left( \dfrac{x+y}{x^2+y^2} \right).
Спасибо за внимание!
Эй, что происходит? Почему от Codeforces остался только вклад, VK CUP и посты на главной разбиты по одному на страницу?
Картинка на случай, если это так выглядит только на моём компе, только в моём браузере, только в моём аккаунте, только в моей стране или ещё что-нибудь подобное.
Наверное, все, кому приходилось писать текст с формулами на Codeforces, знают, что каждую формулу, если это возможно, местный TeX пытается набрать символами, и, только если не получается, вставляет картинку с формулой так, как она бы выглядела в обычном ТеХе. Иногда это выглядит нормально, например, 2·109 (2 \cdot 10^9) или (xi + yi)2 ((x_i+y_i)^2).
Но иногда получается совершенно не то, что вы хотели, например, так:
Cxi + yi - 2xi - 1 (C_{x_i+y_i-2}^{x_i-1}).
В таком случае можно поставить в начале формулы символ \quad. Это, так называемый, "символьный пробел". Он представляет из себя белый квадратик, иными словами, пустой символ, но который при этом не считается пробельным символом. Местный ТеХ по какой-то причине не знает, как этот символ написать и поэтому вставляет формулу в виде картинки в настоящем ТеХовском виде, но символьный пробел игнорируется формулой так же, как и обычный пробел, поэтому на вид формулы это никак не влияет. Получается вот что:
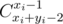 (
(\quad C_{x_i+y_i-2}^{x_i-1}).
560A - Денежная система Геральдиона
Проверьте, есть ли в наборе единица.
560B - Геральд увлекается исскусством
Картины можно прижать друг к другу и поместить на край стенда.
559A - Шестиугольник Геральда & 560C - Шестиугольник Геральда
Пририсуйте к трём сторонам шестиугольника правильные треугольники.
559B - Эквивалентные строки & 560D - Эквивалентные строки
Есть несколько решений. Например, можно проверить, что лексикографически минимальная строка, которая эквивалента первой строке та же, что и у второй.
559C - Геральд и гигантские шахматы & 560E - Геральд и гигантские шахматы
Давайте нижнюю правую клетку тоже покрасим в чёрный цвет и динамикой посчитаем, сколько способов попасть в каждую чёрную клетку, миновав остальные.
В первую очередь, вспомним формулу Пика и будет рассматривать потенциальные стороны многоугольников по-отдельности. А во вторую подумаем, а всех ли их так уж нужно рассматривать?
Освещённая часть тропинки представляет собой объединение отрезков, так что, если бы мы для каждой непрерывной подпоследовательности прожекторов знали, какие отрезки тропинки она может освещать, задача сводилась бы к довольно простой (для задачи с таким номером) динамике.
Как же узнать это? Если брать прожекторы с какого-то момента и добавлять по одному, мы не сможем хранить всю информацию о том, что получается, потому что получается некий набор непересекающихся отрезков и эта сущность слишком многопараметрическая. С другой стороны, если мы добавляем прожектор справа от всех предыдущих и нас интересует, получится ли в конце концов отрезок, то нам важен только левый и правый край освещённой области, а так же самая левая неосвещённая точка между ними.
Доброго всем времени суток!
Приглашаю Вас поучаствовать в 313 Codeforces раунде, над которыми для вас работали я и tunyash. У каждого из нас за плечами по четыре раунда, так что это наш пятый или девятый раунд, как хотите. Я придумал почти все задачи (кроме D div.1), написал условия и разбор всех задач, а tunyash занимался разработкой всех задач.
Gerald уже не является координатором, так что, возможно, Вы по нему соскучились. В этом раунде вы снова с ним встретитесь и поможете ему разобраться в его повседневных жизненных проблемах.
Спасибо координатору Zlobober, нашей переводчице Марии Беловой (Delinur), а так же MikeMirzayanov и всей команде Codeforces за эту платформу.
Этот раунд состоится в необычное время — 17:00 по Московскому времени.
Соревнование закончилось, добро пожаловать в разбор!
Краткий разбор.
Подробный разбор.
Разбалловка в первом дивизионе будет следующая:
500 — 1000 — 1500 — 2250 — 2250
А во втором дивизионе — стандартная:
500 — 1000 — 1500 — 2000 — 2500
Желаю всем получить удовольствие от решения задач!
Поздравляем победителей!
Div. 1:
1. jqdai0815
2. qwerty787788
3. SirShokoladina
4. ainu7
5. Endagorion
Div. 2:
1. goons_will_rule
2. lbn187
3. crawling
4. loveannie
5. Jagabee
560A - Денежная система Геральдиона
В этой задаче главное — заметить, что если есть купюра номинала 1, то любую сумму денег можно выдать единичными купюрами. Если же такой купюры нет, то как раз сумму 1 представить нельзя. Поэтому, если нет купюры номинала 1, то ответ — 1, а если такая купюра есть — то -1.
560B - Геральд увлекается исскусством
Легко заметить, что можно прижать две картины друг в другу какими-то двумя краями, например, разместить одну картину прямо над другой. Тогда высота двух картин будет суммой высот картин, а ширина — максимум из ширин картин. Осталось перебрать все варианты, как повёрнуты картины и как при этом повёрнут стенд. Вот реализация.
559A - Шестиугольник Геральда & 560C - Шестиугольник Геральда
Сперва заметим, что если правильный треугольник с целой стороной k отрезками, параллельными сторонам, разделить на правильные треугольники со стороной 1 (тут появляется картинка), то площадь большого треугольника будет в k2 раз больше площадей маленьких треугольничков и, следовательно, треугольник окажется разделён ровно на k2 единичных треугольничков.
Далее, заметим, что если к сторонам a1, a3 и a5 шестиугольника пририсовать по правильному треугольнику со сторонами a1, a3 и a5 соответственно (и тут появляется ещё одна картинка), то получится большой правильный треугольник со стороной a1 + a2 + a3. Таким образом, площадь исходного шестиугольника равна (a1 + a2 + a3)2 - a12 - a32 - a52.
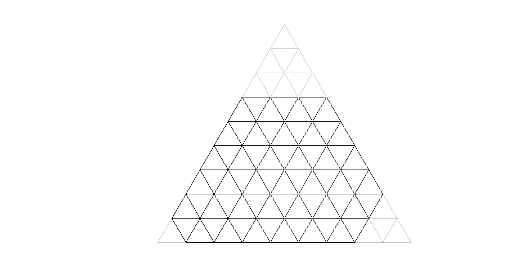
559B - Эквивалентные строки & 560D - Эквивалентные строки
Нетрудно заметить, что "эквивалентность", описанная в задаче, в самом деле является отношением эквивалентности, то есть, оно симметрично, транзитивно и рефлексивно. Подробнее от отношениях эквивалентности можно почитать здесь. В частности, это означает, что все строки разбиваются на классы эквивалентности и нам надо проверить, что данные нам две строки принадлежат одному и тому же классу. Для этого давайте найдём лексикографически минимальную строку, которая лежит в одном классе эквивалентности с каждой из строк. Иными словами, найдём лексикографически минимальную строку, эквивалентную каждой из данных строк и проверим, получилась ли одна и та же строка.
Осталось научиться находить лексикографически минимальную строку, эквивалентную данной, за приемлемое время. Это можно сделать, например, следующей рекурсивной функцией:
String smallest(String s) {
if (s.length() % 2 == 1) return s;
String s1 = smallest(s.substring(0, s.length()/2));
String s2 = smallest(s.substring(s.length()/2), s.length());
if (s1 < s2) return s1 + s2;
else return s2 + s1;
}
Поскольку каждый рекурсивный вызов работает линейно от длины переданной ему строки и внутри функции она сама два раза вызывается от вдвое меньшей строки, эта функция работает за время 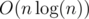 , где n — длина строки.
, где n — длина строки.
559C - Геральд и гигантские шахматы & 560E - Геральд и гигантские шахматы
Обозначим все чёрные клетки как A0, A1, ..., Ak - 1. Для начала, упорядочим чёрные клетки в порядке сверху вниз, а те, которые на одной высоте — слева направо. Теперь все чёрные клетки, из которых пешка Геральда могла бы попасть в данную чёрную клетку, находятся до неё. Покрасим нижнюю правую клетку в чёрный цвет и тоже добавим её в список чёрных клеток под номером k. Теперь пешке Геральда надо попасть в последнюю чёрную клетку, миновав все остальные.
Посчитаем величину Di — количество способов попасть в Ai, миновав все предыдущие чёрные клетки. Как несложно заметить, ответом на задачу будет Dk. Общее количество способов дойти из клетки (1, 1) в клетку (xi, yi) равно 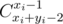 . Вычтем из этого количества все способы попасть в Ai, зайдя по пути в одну из предыдущих чёрных клеток. Для этого переберём, какая из чёрных клеток могла первой попасться на пути. Это должна быть какая-то из предыдущих чёрных клеток, находящаяся не ниже и не правее, чем Ai. Для каждой такой клетки Aj надо вычесть произведение количества способов попасть в Aj, минуя все предыдущие чёрные клетки и количества способов просто попасть из Aj в Ai.
. Вычтем из этого количества все способы попасть в Ai, зайдя по пути в одну из предыдущих чёрных клеток. Для этого переберём, какая из чёрных клеток могла первой попасться на пути. Это должна быть какая-то из предыдущих чёрных клеток, находящаяся не ниже и не правее, чем Ai. Для каждой такой клетки Aj надо вычесть произведение количества способов попасть в Aj, минуя все предыдущие чёрные клетки и количества способов просто попасть из Aj в Ai.
Для вычисления биномиальных коэффициентов придётся преподсчитать факториалы всех чисел до 2·105 и научиться брать обратные к ним по модулю 109 + 7.
Для начала, вспомним формулу Пика. Благодаря ней, количество целых точек внутри любого многоугольника можно вычислить, зная его площадь и количество целых точек на границе. Количество целых точек на отрезке, соединяющем точки (0, 0) и (a, b) можно посчитать, найдя НОД(a, b).
Давайте вычислим общее количество целых точек в основном многоугольнике, а затем для каждого отрезка, соединяющего какие-то две вершины многоугольника, вычтем из этой величины произведение вероятности того, что этот отрезок будет стороной выбранного многоугольника и количество целых точек в сегменте основного многоугольника, который отсекает этот отрезок.
Вероятность легко посчитать. Если отрезок соединяет вершины Ai и Ai + k, то существует ровно 2n - k - 1 - 1 многоугольник, в котором есть такая сторона, а общее количество валидных многоугольников равняется 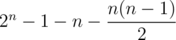 .
.
Количество целых точек в отсекаемом отрезком AiAi + k сегменте тоже легко посчитать с помощью с формулы Пика за время O(k), а если воспользоваться тем, что перед этим мы посчитали количество целых точек в сегменте, отсекаемом AiAi + k - 1, можно сделать это за время O(1).
Таким образом, получается решение за время 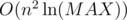 (
(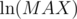 -- время вычисления НОД двух натуральных чисел, не превосходящих MAX). Это, конечно, слишком много.
-- время вычисления НОД двух натуральных чисел, не превосходящих MAX). Это, конечно, слишком много.
Давайте обратим внимание на вероятность появления каждой из сторон. Вероятность появления в многоугольнике стороны, пропускающей k - 1 вершину многоугольника, равна 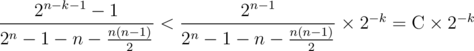 . Как видно, эта вероятность экспоненциально падает с ростом k. В частности, если общее количество целых точек в многоугольнике равно V, то сумма всех слагаемых, соответствующих отрезкам с k ≥ 60 не превосходит
. Как видно, эта вероятность экспоненциально падает с ростом k. В частности, если общее количество целых точек в многоугольнике равно V, то сумма всех слагаемых, соответствующих отрезкам с k ≥ 60 не превосходит 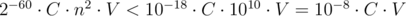 . Таким образом, все слагаемые, соответствующие отрезкам с k ≥ 60, можно просто игнорировать. Следует отметить, что 60 — это очень грубая оценка, не учитывающая, что для большинства отрезков вероятность будет гораздо меньше, чем 2 - 60, а для отрезков с k порядка 60 количество целых точек внутри сегмента будет порядка
. Таким образом, все слагаемые, соответствующие отрезкам с k ≥ 60, можно просто игнорировать. Следует отметить, что 60 — это очень грубая оценка, не учитывающая, что для большинства отрезков вероятность будет гораздо меньше, чем 2 - 60, а для отрезков с k порядка 60 количество целых точек внутри сегмента будет порядка 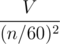 , а вовсе не порядка V.
, а вовсе не порядка V.
Таким образом, мы получаем решение за время 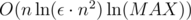 , поскольку 60 — это ни что иное, как
, поскольку 60 — это ни что иное, как 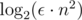 .
.
Освещённая часть тропинки представляет собой объединение нескольких непересекающихся освещенных отрезков (возможно, одного). Давайте упорядочим прожекторы по возрастанию ai. Заметим, что каждый освещенный отрезок освещается некоторой "подстрокой" прожекторов, то есть, множеством прожекторов с номерами из некоторого отрезка [l, r]. Пусть x0, ..., xk — упорядоченная последовательность потенциальных концов отрезков, то есть, всех чисел вида ai - li, ai и ai + li.
Представим себе, что мы знаем, какие именно отрезки тропинки можно осветить с помощью каждой подстроки прожекторов. Сохраним в массив left[][][] информацию о самых длинных возможных освещенных отрезках в следующем виде: left[l][r][j] — самое маленькое такое i, что подстрока [l, r] прожекторов может освещать отрезок [xi, xj].
Теперь, имея массив left, посчитаем динамикой величину best[R][i] — какую максимальную длину тропинки можно осветить, используя первые L прожекторов так, чтобы самой правой освещённой точкой была xi. Это легко сделать за время O(n4), так как 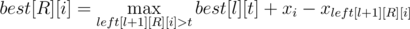 .
.
Теперь давайте вычислим массив left. Рассмотрим некую подстроку прожекторов [l, r]. Пусть все прожекторы этой подстроки как-то ориентированы и освещают некоторую область тропинки. У этой области можно рассмотреть самую левую (i) и самую правую (j) освещенную точки, а также правый конец самого левого освещенного отрезка (t). Если область является одним отрезком, то t = j. Рассмотрим, как меняются эти три параметра, когда мы добавляем к подстроке прожектор r + 1 и выбираем его ориентацию. К освещенной области добавляется отрезок [a, b], который равен [ai - li, ai] или [ai, ai + li]. Самая левая освещенная точка становится min(a, xi), самая правая — max(b, xj). А правый конец самого левого отрезка не меняется, если a > t или становится b, если a ≤ t.
Эти соотношения позволяют для каждого фиксированного L вычислить динамикой величину dp[r][j][y] — наименьшее такое i, что можно ориентировать прожекторы подстроки [L, r] так, чтобы самая левая освещенная точка была xi, самая правая — xj, а правый конец самого левого отрезка — xt. Вычислив это, уже легко посчитать значения массива left[L][][]. Эта часть решения тоже будет работать за время O(n4).
По-моему, давно пора бы ввести в обиход сленговые названия для задач определённого типа. Например:
Задача-паззл: задача, решение которой состоит из большого числа маленьких простых частей, которые замучаешься писать.
Задача-бигмак: задача, к который ты не знаешь, как подступиться, с какой стороны на неё не посмотри.
Задача-бильярдный шар: задача, авторское решение которой работает на миллисекунду быстрее, чем TL.
Задача-реферат: задача, в которой надо скопировать код с e-maxx'а и немного его подправить.
Задача-пицца: задача, ключевая формула для решения которой написана прямо в условии.
Задача-шифровка: задача, самое трудное в решении которой — понять условие.
Ещё какие-нибудь?
На днях случился отборочный раунд RCC. Волею судеб мне пришлось писать его в рейсовом автобусе и я решил поделиться с вами своим опытом.
Обычно я не пишу контесты по дороге, в кафешках, в шуме, с мобильника и прочих подобных условиях, но это был отборочный раунд RCC, так что я решил попробовать.
По счастью, как раз в 13:00 автобус сделал остановку на 40 минут, так что начался контест спокойно. Интернет с мобильника, на удивление, был достаточно стабильным, с этим проблем не было. Ноут лежал на коленях и был менее зафиксирован, чем я к тому привык, но к этому легко удалось удалось адаптироваться — достаточно было не опираться на него руками. Был яркий солнечный день и экран бликовал, тем более, что мне пришлось немного убавить яркость, чтобы зарядки хватило на 3 часа, однако, и к этому удалось довольно легко адаптироваться, скоро я перестал замечать блики. В общем, первые 45 минут прошли довольно успешно, я сдал А и почти дописал В. Вокруг шумели дети, которых мы везли на выезд по по случаю выпускного из 9 класса, но и к этому легко удалось адаптироваться. Можно, конечно, было надеть наушники с музыкой, но этого не потребовалось.
Потом автобус поехал и пол стал дрожать под ногами, а вместе с ним и ноут. Впрочем, эту неприятность тоже было легко обойти, достаточно оказалось печатать, прижимая ноут подушечками ладоней к коленям.
В общем, серьёзных препятствий к написанию программ не было. Однако открылась неожиданная проблема. Я тщётно пытался тестировать решение задачи B и думать о решении задач C и D — выяснилось, что из-за дражание сиденья, которое ощущалось во всём теле, совершенно невозможно было погрузиться в размышления о задачах. Через некоторое время мне пришлось выключить ноут.
А насколько вы терпимы к окружающим условиям во время контеста?
А там e-maxx упал. Кто знает, будет ли он работать? Есть какие-то прогнозы?
1 раунд FHC в этом году пройдёт в субботу 17 января, в 9 вечера по Московскому времени.
Эта и прочая информация есть здесь. Во второй раунд пройдут первые 500 участников, а также все, кто наберёт столько же баллов, сколько и участник на пятисотом месте.
1 раунд продлится 24 часа, и это будет не виртуальный контест, который ты начинаешь в любой момент в течение этих 24 часов, а полноценный 24часовой контест и это весьма неординарное решение. Понятно, что организаторы хотели, чтобы все смогли найти удобное время порешать задачи. Надеюсь, проблемсет будет таким, чтобы состав участников второго раунда не очень зависел от того, кто сможет порешать пару часов, а у кого — весь день свободен. Возможно, предполагается, что будет определённый набор задач, доступный для большого количества участников, гораздо большего, чем 500, но гораздо меньше, чем 500 человек смогут решить что-то ещё.
Процесс творения раунда без прикрас и страшилок.
Путеводитель по творению раунда от автора четырёх Codeforces раундов.
Спасибо RodionGork, который придал мне необходимый испульс и hball1st, который придал необходимый импульс RodionGork.
1. Придумывание задач.
Тут сложно дать какой-то совет. Нет какого-то определённого алгоритма придумывания задач, а если бы он был, получились бы не задачи, а сложные упражнения на стандартные алгоритмы, как половина задач на Russian Code Cup. Чтобы получилась хорошая, интересная задача, должна быть какая-то идея, которая пришла в голову Вам, а потом должна прийти в голову участникам соревнования. Какая-то, хотя и самая элементарная, но идея, в идеале, должна быть даже в задаче A второго дивизиона. Так что, должен сразу предупредить, что, поскольку творческое мышление — процесс, воспитываемый с самого детства, то придумывать задачи дано не всем. Увы.
Мы все давно уже, с появлением Codeforces, оценивая успешность каждого человека в СП, смотрим на два его рейтинга — здесь и на TopCoder. И часто рейтинги сильно различаются. А почему бы не сотворить объединённый рейтинг? Мысленно объединить аккаунты каждого человека на TC и CF и рассматривать все SRM'ы и CFR'ы равноправно. Формулу подсчёта рейтинга можно взять с топкодера, благо она там открыта.
Самая большая проблема — это объединить аккаунты. Поначалу можно объединить по совпадающим никам, а так же аккаунты всем известных личностей (понятно, что могут случится левые объединения, но их будет крайне мало и общей картины это не испортит). Кроме того, добавить общедоступную табличку, куда все, кто хочет, смогут написать своё соответствие.
Я бы рад сам всё это сделать, но времени нет =(
Доброго всем времени суток!
Приглашаю Вас поучаствовать в 194 раунде, автором которого я являюсь. Это мой четвёртый раунд, хотя предыдущие три были очень давно: Codeforces Beta Round 79 (Div. 1 Only), Codeforces Beta Round 94 (Div. 1 Only), Codeforces Round 110 (Div. 1) (прошу прощения у div-2 участников, что упоминаю только div-1 раунды, просто ссылка даже на один раунд уже чересчур громоздка).
В этот раз, как в раунде Codeforces Beta Round 79 (Div. 1 Only), вы вновь поможете мальчику Геральду разобраться с его проблемами. На этот раз его проблемы настолько серьёзны, что он стал координатором контестов на Codeforces и помог мне сделать этот раунд, чтобы спихнуть их на вас.
Хочу поблагодарить Gerald за то, что он очень хорошо выполняет работу координатора. Работая с ним, ощущаешь, что всё действительно под контролем. Кроме того, спасибо Марии Беловой за перевод условий на английский. Также спасибо Seyaua и Aksenov239 за тестирование задач.
Этот раунд состоится в необычное время — 12:30 по Московскому времени.
Разбалловка стандартная, 500 — 1000 — 1500 — 2000 — 2500.
Всем спасибо за участие, добро пожаловать в разбор.
Мои поздравления победителям:
Дивизион 1:
1. KADR
2. RAVEman
3. PavelKunyavskiy
4. Dmitry_Egorov
5. RAD
6. sy2006
7. mmaxio
8. riadwaw
9. niyaznigmatul
10. RomaWhite
Отдельно хочу отметить сразу двух украинских участников, которым единственным покорились все пять задач!
Дивизион 2:
1. IMOiguanas
2. savsmail
3. suyash666
4. AntiForest
5. kang205
6. jschnei
7. littlepanda
8. langdamao
9. 9mmlitswe
10. Renkai
Недавно я впервые стал красным на топкодере. Конечно, сам по себе этот факт мало кому интересен. Интересно другое: став красным, я стал уникальным (ли?) обладателем всех пяти цветов (в разные моменты времени, конечно):
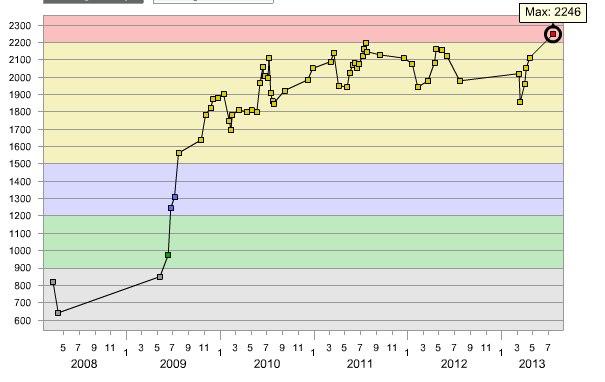
Жаль, что в Record Book нет пункта "повышение рейтинга в как можно большее количество раз" — я бы наверняка туда попал.
Кто-нибудь видел ещё столь же разноцветных людей на TopCoder'е или на Codeforces'е?
В этой задаче требуется разделить все натуральные числа от 1 до n2 на n групп по n чисел в каждой так, чтобы суммы чисел во всех группах были одинаковыми.
Давайте разобьем все эти числа на пары 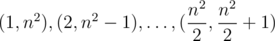 . Это можно сделать благодаря тому, что n четное, а значит, и n2 тоже. Сумма каждой из этих пар равна n2 + 1. Теперь осталось только определить по
. Это можно сделать благодаря тому, что n четное, а значит, и n2 тоже. Сумма каждой из этих пар равна n2 + 1. Теперь осталось только определить по  пар в каждую из групп.
пар в каждую из групп.
В этой задаче требуется сделать лишь то, что сказано — определить, удовлетворяет ли данный набор из восьми точек описанному условию.
Есть множество способов это сделать. Например, следующий:
Проверить, что среди координат этих точек есть ровно три различных x и ровно три различных y. Найти количество различных x (так же, как и y) можно, положив их в set и узнав его размер. Если оно не равно 3, вывести <>.
Итак, у нас есть x1, x2 и x3, а так же y1, y2 и y3. Осталось проверить, что для любой пары (xi, yj) (кроме (x2, y2)) данная точка присутствует среди восьми перечисленных. Можно просто перебрать все эти пары и для каждой пары, перебрав все восемь точек, выяснить, есть ли эта пара.
Однако я думаю, что читать решение в данном случае — неблагодарная затея. Лучше просто посмотреть реализацию.
334C - Секреты / 333A - Секреты
На самом деле, в задаче разыскивается самая длинная такая последовательность натуральных чисел a1, a2, ..., ak, такая, что каждое число в ней является степенью тройки, сумма всех чисел больше, чем n, и если выкинуть любое из чисел, то сумма станет меньше n. Если точнее, требуется лишь узнать длину этой последовательности.
Рассмотрим минимальное ai = A. Поскольку все эти числя являются степенями 3, то все остальные ai делятся на A и, следовательно, сумма всех этих чисел S тоже делится на A. Если n также делится на A, то, так как S > n, то S превосходит n как минимум на A. Следовательно, если выкинуть из последовательности число A, то остаток будет не меньше, чем n, а это противоречит второму условию. Таким образом, мы выяснили, что n не делится ни на одно из чисел этого последовательности, даже на самое маленькое. Тогда найдем минимальное k такое, что 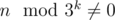 — это легко сделать простым перебором. А дальше просто набрать минимальную сумму, превосходящую n монетами номинала 3k. Таким образом, ответом будет число
— это легко сделать простым перебором. А дальше просто набрать минимальную сумму, превосходящую n монетами номинала 3k. Таким образом, ответом будет число 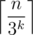 .
.
В этой задаче требовалось найти максимальное количество фишек, которые Геральд может поставить на поле.
Сначала сделаем два замечания.
- На каждую линию (вертикаль или горизонталь) можно поставить только одну фишку, с одного конца или с другого.
- Если на линии есть хотя бы одна запрещенная клетка, то на нее нельзя поставить ни одной фишки.
Соблюдая последнее замечание, мы избегнем попадания фишек на запрещенные клетки. Осталось избежать <<столкновения>> фишек.
Рассмотрим следующие четыре линии: вертикали i и n + 1 - i и горизонтали с теми же номерами (i может быть любым, если только i ≠ n + 1 - i). Заметим, что фишки, поставленные на эти линии, могут столкнуться друг с другом, но не могут столкнуться с фишками на других линиях. Таким образом, для этих четырех линий можно решать задачу независимо от других линий. Осталось заметить, что мы можем поставить фишки на каждую из этих линий (на которой не стоит запрещенная клетка), так, чтобы они не столкнулись так, как это показано на картинке.
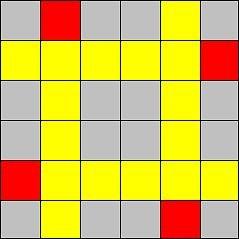
Итого, можно просто перебрать эти четверки линий и для каждой из них выяснить, сколько фишек можно на них поставить. И не забыть рассмотреть случай двух средних линий в случае нечётного n.
334E - Счастливые билеты / 333C - Счастливые билеты
В это задаче надо предъявить нужное количество счастливых билетов.
Давайте рассмотрим, сколько разных чисел можно получить таким образом из четырёхзначных номеров. Их легко перебрать, благо их всего 104. Оказывается, что в среднем получается почти 60 чисел на каждый четырёхзначный номер. Пусть из номера n можно получить число x. Ясно, что k - x ≥ 0 либо x - k ≥ 0. Если, например, k - x ≥ 0, мы можем записать восьмизначный номер, в первых четырех цифрах которого будет записано k - x, а в последних четырех — n. Понятно, что такой билет будет k-счастливым. Всего это дает нам почти 600 000 билетов, этого вполне достаточно.
333D - Характеристики прямоугольников
По сути, в этой задаче надо найти, каким наибольшим может быть значение минимума из четырех клеток на пересечении двух столбцов и двух строк.
Иными словами, надо найти максимальное значение величины min(ai1, j1, ai1, j2, ai2, j1, ai2, j2) при всех i1, i2, j1, j2 таких, что 1 ≤ i1, i2 ≤ n, 1 ≤ j1, j2 ≤ m, i1 ≠ i2, j1 ≠ j2. Давайте применим бинарный поиск по ответу. Для этого надо научиться находить, есть ли в таблице из 0 и 1 два столбца и две строки, на всех четырех пересечениях которых стоят единицы, то есть, такие i1, i2, j1, j2, что ai1, j1 = ai1, j2 = ai2, j1 = ai2, j2 = 1. Давайте рассмотрим все такие пары натуральных чисел (i1, i2), что существует натуральное число j такое, что ai1, j = ai2, j = 1. Наличие двух одинаковых таких пар как раз и означало бы наличие вышеописанных четырех чисел. Однако, всего может быть 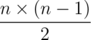 таких пар. Следовательно, мы можем завести массив, где будем отмечать, какие пары уже встретились и перебирать все пары в любом порядке, пока не встретится повторяющаяся пара или пока все пары не будут перебраны. Итого, получаем решение за время
таких пар. Следовательно, мы можем завести массив, где будем отмечать, какие пары уже встретились и перебирать все пары в любом порядке, пока не встретится повторяющаяся пара или пока все пары не будут перебраны. Итого, получаем решение за время 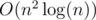 .
.
В этой задаче требуется нарисовать три непересекающихся круга максимального радиуса с центрами в заданных точках. Иными словами, нам надо найти треугольник у которого минимальная из сторон будет максимальна.
К сожалению, мы не ожидали решения с битовой оптимизацией, которое оказалось для участников проще нашего.
Вспомним факт из школьного курса геометрии, говорящий, что напротив большего угла лежит большая сторона. Кроме того, вспомним, что сумма углов в треугольнике равна 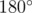 . Из этого следует, во-первых, что как минимум один угол в треугольнике не меньше
. Из этого следует, во-первых, что как минимум один угол в треугольнике не меньше 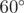 . Во-вторых, что этот угол не может быть самым маленьким в треугольнике. И следовательно, что напротив этого угла лежит не самая маленькая сторона. Следовательно, если в
. Во-вторых, что этот угол не может быть самым маленьким в треугольнике. И следовательно, что напротив этого угла лежит не самая маленькая сторона. Следовательно, если в 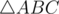
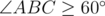 , то min(|AB|, |BC|, |CA|) = min(|AB|, |BC|).
, то min(|AB|, |BC|, |CA|) = min(|AB|, |BC|).
Следовательно, мы можем поступить следующим образом. Переберем вершину B и найдем треугольник с максимальной минимальной стороной среди таких, у которых 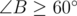 . Для этого отсортируем все остальные вершины по углу относительно B, и для каждой вершины A найдем самую удалённую от B вершину C среди отрезка тех вершин, для которых
. Для этого отсортируем все остальные вершины по углу относительно B, и для каждой вершины A найдем самую удалённую от B вершину C среди отрезка тех вершин, для которых 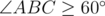 . Для этого нам понадобится использовать дерево отрезков для максимума и два указателя или бинарный поиск, чтобы хранить левую и правую границу возможных вершин C при переборе вершины A.
. Для этого нам понадобится использовать дерево отрезков для максимума и два указателя или бинарный поиск, чтобы хранить левую и правую границу возможных вершин C при переборе вершины A.
Итого, получаем решение за время 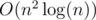 .
.
Мне кажется, что было бы удобно на главной страничке раунда отображать дату раунда. Можно, например, под фразой "Codeforces Round #N" поместить ещё одну строчку, что-нибудь в стиле: "15 апреля 2011 года, начало в 22:00, длительность 2:10".
Иногда это бывает интересно знать, но нет никакого простого способа это выяснить. Сейчас можно только перейти в материалы раунда (если они есть, но они могут быть опубликованы в другой день и уж точно в другое время), либо покопаться в списке "соревнования".
Итак, давайте поговорим о том, как следует оценивать штрафные попытки по задачам.
Толчком к подобным размышлениям служит следующая мысль. С точки зрения "качества программирования", если можно так выразиться, есть большая разница между задачей, сданной с первой же попытки и задаче, сданной после одной неверной попытки. Тогда как сдана задача с 10 или 11 попытки — существенной разницы нет. Однако же, разница в баллах сейчас одна и та же: 50 баллов (если, конечно, стоимость задачи ещё не опустилась до 30% стоимости задачи). В связи с этим, есть следующее конструктивное предложение: сделать стоимость минусов убывающей.
Например, если задача имеет стоимость 1000, это может выглядеть так:
| номер попытки | штраф за минус | суммарный штраф |
| 1 | 100 | 100 |
| 2 | 79 | 179 |
| 3 | 62 | 241 |
| 4 | 50 | 291 |
| 5 | 39 | 330 |
| 7 | 25 | 386 |
| 10 | 12 | 432 |
| 15 | 3 | 461 |
| 20 | 1 | 469 |
| > 20 | 0 | 469 |
Примерно такие значения получаются, если предположить, что стоимость минуса будет убывать в геометрической прогрессии, уменьшаясь в два раза после каждых трёх минусов.
Таким образом получается, что минусы после 20ого (часто ли вы такое видите?) даются бесплатно. Получение трёх минусов карается четвертью стоимости задачи, пяти — третью стоимости, а сделав двузначное число штрафных попыток, Вы теряете почти половину стоимости задачи.
A (Div2) Результат игры
В этой игре можно было просто сделать, то, что просят в условии.А именно, завести счётчик, перебрать все клетки поля, и для каждой клетки найти сумму чисел в клетках, стоящих с ней на одной горизонтали, сумму чисел в клетках, стоящих с ней на одной вертикали, и сравнить эти суммы. Если сумма по вертикали больше, увеличить счётчик на один. После того, как перебраны все клетки, вывести счётчик. Максимальная сумма может быть 2 × 30 × 100 = 6 000, поэтому для её достаточно типа int.
B (Div2) След
Извиняюсь за кривой
Давайте для начала отсортируем радиусы окружностей по убыванию. Пусть у нас теперь радиус первой окружности — r1, второй окружности — r2, ..., последней окружности — rn, где r1 > r2 > ... > rn. Внешняя область — так, которая снаружи первой окружности — покрашена в синий цвет, значит, область между первой и второй окружностью покрашена в красный. Далее, область между второй и третьей окружностью покрашена в синий цвет, между третьей и четвёртой — в красный, между четвёртой и пятой — в синий, и так далее.
Первая область, закрашенная в красный цвет (область между первой и второй окружностями) — это вся область внутри первой окружности, из которой выкинули внутреннюю область второй окружности. Значит, площадь это области равна π × (r12 - r22). Аналогично, площадь второй красной области (между третьей и четвёртой окружностями) равна π × (r32 - r42). И так далее. Значит, суммарная их площадь равна π × (r12 - r22 + r32 - r42 + r52 - r62 + ...). Значит, чтобы посчитать ответ можно, например, сложить квадраты радиусов окружностей с нечётным номером, вычесть из полученной суммы квадраты радиусов всех окружностей с чётными номерами, и полученную величину умножить на \pi.
Может возникнуть небольшое затруднение с последней окружностью. Если число окружностей нечётно, то последняя область — не кольцо между двумя окружностями, а круг. Но это, на самом деле, ничего не меняет: тогда последняя окружность имеет нечётный номер, и квадрат её радиуса надо тоже прибавить к сумме.
A (Div1) — C (Div2) Сообщение
Для начала, добавим к строке s с обоих концов по 2000 фиктивному символу — например, <<#>>. Заметим, что это не повлияло на ответ. Действительно, пусть мы взяли подстроку t, частично или полностью состоящую из <<#>>. Тогда все символы <<#>> надо было бы заменить. Но если бы их просто не было, то нужные символы надо было бы добавить.
Рассмотрим оптимальную подстроку t, и последовательность действий, которую надо с ней сделать, чтобы превратить её в строку u. Рассмотрим первое добавление или удаление символа с одного из концов.
Заметим, что это не удаление. Ведь если мы выбрали подстроку t и удалили из неё, к примеру, последний символ, то его не надо было бы и брать, потому что для строки t без последнего символа надо на одно действие меньше, чем для всей строки t.
А теперь заметим, что это и не добавление. Действительно, пусть мы рассмотрели строку t, некоторое время меняли в ней символы на другие, и наконец, добавили один, скажем, в начале. Тогда - Если слева от строки есть символ (то есть, строка там ещё не кончается), то можно было его взять сразу (то есть, рассмотреть не t, а t с ещё одним символом слева). Вместо того, чтобы добавлять символ, можно заменить существующий — это тоже занимает одной действие. - Если слева от строки нету символа (то есть, первый символ t является первым символом строки s), тогда в t есть как минимум 2000 <<#>>. Значит, либо ответ для такой строки как минимум 2000, потому что каждую решётку надо удалить или заменить; либо никаких символов, кроме решёток, в строке t нет, и тогда надо сделать как минимум |u| действий, потому что каждый символ u надо добавить (или сделать из другого символа). Но чтобы получить всего |u| действий, достаточно взять любую подстроку длины |u|.
Таким образом, существует оптимальная подстрока t, из которой получается u без добавлений и удалений. Это ключевой момент решения! Ведь это означает, что длина такой строки равна длине u. Значит, достаточно перебрать подстроки строки s длины |u|. Всего таких подстрок O(|s|), и для каждой подстроки легко за время O(|u|) посчитать необходимое количество изменений — это просто количество символов, которые надо заменить.
Таким образом, получается очень простое в написании решение за время O(|s| × |u|).
B (Div1) — D (Div2) Подозреваемые
Будем называть людей, которые сказали <<Убийство совершил подозреваемый номер ai>> обвиняющими, а людей, которые сказали <<Подозреваемый номер ai не совершал убийства>> — оправдывающими. Рассмотрим подозреваемого номер k. Предположим, что он совершил убийство и посчитаем, сколько тогда человек сказали правду. Люди, которые сказали правду — это люди, которые обвиняли его, и люди, которые оправдывали не его. Таким образом, их количество — это количество людей, которые обвинили его, плюс количество людей, которые оправдали кого-либо, и минус количество людей, которые оправдали его. Таким образом, нам надо знать - количество людей, которые кого-либо обвиняют (это легко посчитать за O(n)) - для каждого подозреваемого количество людей которые его обвиняют - для каждого подозреваемого количество людей которые его оправдывают Последние две величины легко посчитать за время O(n) для всех подозреваемых. Действительно, пусть i-того человека обвиняют xi людей и оправдывают yi людей. Тогда надо просто для каждого человека номер i, если он оправдывающий, то увеличить yai, а если обвиняет — увеличить xai.
После этих действий можно за O(1) посчитать для каждого подозреваемого число людей, которые говорят правду в том случае, если он преступник, и если это количество равно m, то данный человек может быть преступником. А после того, как мы нашли список возможных преступников, то не составляет труда для каждого человека определить, может ли он говорить правду и может ли он врать.
С (Div1) — E (Div2) Шифр
Давайте в словах записывать вместо букв цифры: вместо <> — 0, вместо <> — 1, и так далее. Тогда разрешенные операции такие: рассмотреть два соседних числа, и одно из них увеличить на один, а другое — уменьшить на один. Для начала докажем ключевое утверждение задачи: два слова имеют одинаковый смысл тогда и только тогда, когда у них одинаковая длина и одинакова сумма букв.
Я мог бы привести полное и строгое доказательство этого факта, но оно будет длинным и немного занудным и, думается мне, его вряд ли кто-нибудь будет читать. Лучше я просто опишу две переформулировки задачи, в которых этого утверждение становится более очевидным.
1. Переформулировка первая. Представим себе, что у нас вместо каждого числа — стопка монет, от 0 до 25 штук. Тогда разрешенные действия — это переложить одну монету из какой-то стопки в соседнюю так, чтобы во всех стопках оставалось от 0 до 25 монет.
2. Переформулировка вторая. Рассмотрим последовательность si (i = 0, ..., n), такую, что si равно сумме первых i чисел в слове. Последовательность неубывает и разность между соседними элементами последовательности не превосходит 25. Тогда разрешенная операция — это изменить одно из чисел на один в любую сторону, так, чтобы разность между любыми двумя соседними числами по-прежнему не превосходила 25, и последовательность по-прежнему неубывала.
Таким образом, нам надо посчитать, сколько слов такой же длинны имеют такую же сумму букв. Это легко сделать сразу для всех слов длины не больше 100. Посчитаем с помощью динамики такую величину x[l][s] : количество слов длины l с суммой букв s. - База динамики: l = 0. Есть ровно одно слово (пустое, оно же единственное слово длины 0) с суммой букв 0, и по 0 слов с любой другой суммой букв. - Переход динамики: очень простой. Чтобы узнать, сколько слов длины l имеют сумму s, надо перебрать, какая может быть последняя буква у этого слова: x[l][s] = x[l - 1][s] + x[l - 1][s - 1] + ... + x[l - 1][s - 25]. Конечно, надо не забыть считать эту величину по модулю 109 + 7.
После того, как мы посчитали эту величину для всех 0 ≤ l ≤ 100, 0 ≤ s ≤ 2500 за O(1002 × 25) памяти и O(1002 × 252) времени, надо просто для каждого слова найти его длину сумму букв и вывести ответ (не забыв вычесть 1).
D (Div1) Улики
Как придумать формулу
Простите все, кому это непривычно, но поскольку интерпретатор ТеХа на Codeforces в данный момент несколько кривоват, вместо традиционных нижних индексов будут нетрадиционные верхние. Это не степени, о степенях я буду оповещать отдельно.
Говоря математическим языком, в задаче надо посчитать количество способов дополнить граф до связного минимальным количеством ребер. Понятно, что сам граф не имеет значения — важны только компоненты связности. Более того, сами компоненты связности не важны, важны только их размеры.
Итак, пусть у нас есть k компонент связности размера s1, s2, ..., sk.Посмотрим, чем равна искомая величина для маленьких k.
Пусть k = 1. Тогда граф уже связный, есть 1 способ добавить ноль ребер.
Пусть k = 2. Тогда в графе две компоненты связности и надо добавить одно ребро между ними. Существует s1 способ выбрать вершину из первой компоненты, s2 способов — из второй, всего s1s2 способов.
Пусть k = 3. Тогда в графе три компоненты связности, и надо провести два ребра, которые будут соединять различные пары компонент связности. Общее количество способов будет равно s1s2 × s1s3 + s1s2 × s2s3 + s1s3 × s2s3 = s1s2s3 × (s1 + s2 + s3) = s1s2s3 × n.
Участники с самой богатой фантазией могли уже сейчас догадаться до правильной формулы. Но лучше посмотрим на следующее значение k:
Пусть k = 4. Тогда в графе 4 компоненты связности размера s1, s2, s3, s4. Надо провести три ребра. Немного подумав, можно понять, что эти рёбра либо будут соединять одну из компонент связности с остальными тремя, либо первую со второй, вторую — с третьей, а третью — с четвёртой (разумеется, компоненты могут следовать в любом порядке).
Количество способов первого типа: (s1)3 × s2s3s4 + (s2)3 × s1s3s4 + (s3)3 × s1s2s4 + (s4)3 × s1s2s3 = ((s1)2 + (s2)2 + (s3)2 + (s4)2) × (s1s2s3s4).
Количество способов второго типа: есть две компоненты связности, из которых выходит по два ребра. Пусть это первая и вторая. Тогда одно ребро проведено между ними, и ещё одно — из них в другие компоненты связности. Эти два ребра могут быть проведены двумя способами: от первой к третьей, а от второй к четвёртой, или наоборот. Значит, количество таких способов равно 2 × (s1)2 × (s2)2 × s3 × s4 = 2s1s2 × (s1s2s3s4). И Таких слагаемых 6 штук. Просуммировав их всех и прибавив к ним способы первого типа, можно вынести множитель (s1s2s3s4) за скобки, и останется аккурат формула квадрата суммы 4-х слагаемых. Значит, общее количество способов будет равно (s1s2s3s4) × n2.
На этом месте можно было уже легко догадаться до формулы (s1s2... sk) × nk - 2, тем более, что в первом случае получается как раз 1 = (s1) × n - 1.
Как доказать формулу
Осталось только эту формулу доказать (хотя, конечно, для того, чтобы сдать задачу, доказательства не требовалось =))
Итак, пусть есть некий набор из k - 1 ребра, который дополняет граф до связного. Построим по нему две последовательности чисел: (x^1, x^2, ..., x^{k-2}) и (a^1,a^2,...,a^k). При это каждое x может быть любым числом от 1 до n, а ai может быть любым числом от 1 до si. Легко понять что таких пар последовательностей аккурат столько же, сколько (якобы!) способов дополнить наш граф до связного.
Пара последовательностей же строится следующим образом.
Для начала заметим, что этот набор из k - 1 ребра как бы образует дерево, в вершинах которого — компоненты связности.
Рассмотрим минимальную по номеру компоненту связности, из которой выходит только одно дополняющее ребро. Пусть это компонента номер i и ребро соединяет вершину номер t в компоненте номер i и вершину номер b в другой компоненте. Тогда x1 = b, а ai равно (внимание!) номеру вершины t среди вершин компоненты i, то есть, числу от 1 до si.
Одна из компонент связности теперь отвалилась от графа. Остальные k - 2 ребер дополняют оставшиеся k - 2 компоненты до связного графа. Повторим ту же процедуру еще k - 1 раз.
Осталось одно ребро. Оно соединяет две компоненты связности u и v, которые ещё не упомянуты во второй последовательности. Первая же последовательность заполнена — в ней как раз k - 2 элемента. Осталось во вторую последовательность на места номер u и v записать номера концов оставшегося ребра среди вершин компонент номер u и v соответственно.
Итого, для каждого способа дополнить граф до связного существует такая пара последовательностей. Заметим, что если компонента i была <<висячей>>, то есть, соединялась только с одной другой компонентой, то её вершины не упоминаются в первой последовательности. А если не была висячей — то упоминаются, потому что все рёбра, которые выходят из этой компоненты, надо выкинуть. Каждое ребро, которое мы выкидываем, упирается одним концов в висячую компоненту. И когда было выкинуто первое ребро, выходящее из компоненты i, компонента i не была висячей. Значит, при выкидывании этого ребра в первую последовательность была записана вершина из компоненты i.
Более того, как следует из рассуждений выше, в любой момент в процессе записи первой последовательности, если выясняется, что в ней больше не будет упомянуты вершины из компоненты i, то это означает, что компонента i либо уже выкинута, либо в данный момент висячая.
Значит, в начальный момент, и каждый момент в процессе построения первой последовательности, по оставшемуся куску последовательности можно судить, какие вершины в данный момент висячие.
Итак, пусть у нас есть какой-то, неизвестный способ дополнить граф до связного и мы построили по нему две последовательности (x1, x2, ..., xk - 2) и (a1, a2, ..., ak). Восстановим по ним дополнение графа до связного.
Рассмотрим x1. Это число говорит нам, что сначала было выкинуто ребро одним концом в x1, а другим — в наименьшей по номеру висячей компоненте связности. Мы можем её определить, так как знаем текущий список висячих компонент. Пусть это компонента i. Тогда в ai записан номер вершины в компоненте i, которая соединена с x1. Итак, одно ребро восстановили. Выкидываем компоненту номер i.
Делаем эту операцию ещё k - 1 раз. Выкинуты k - 2 компоненты и восстановлены k - 2 ребра. Осталось два неиспользованных элемента второй последовательности, которые определяют вершины в двух оставшихся компонентах. Эти вершины и надо соединить k - 1-ым ребром.
Итого, по каждой паре последовательностей восстанавливается дополнение до связного графа, из которого эта пара последовательностей была получена. Значит, количество способов дополнить граф до связного равно количеству пар последовательностей, которое и равно (s1s2... sk) × nk - 2.
E (Div1) Оладьи миссис Хадсон
Для начала заметим, что легко придумать очень простое решение этой задачи. Можно просто хранить остаток от деления каждой из цен на каждое из 25 простых чисел от 2 до 97. Тогда каждый запрос будет выполняться за O(25 × 10000). И всего решение будет работать за O(25 × 10000 × 30000) = O(7, 5 × 109) взятий по модулю. К сожалению, это не укладывается в ограничение по времени =)
Первая идея авторского решения: если результаты наших действий класть с мап и доставать оттуда при необходимости, это сильно ускорит работу программы. Но мапить надо с умом! Во-первых, надо класть в мап остатки от произведения цен баночек, подходящих под шаблон, по модулю простых чисел. Во-вторых, все шаблоны, под которые подходят все номера, надо считать идеинтичными, независимо от основания системы исчисления.
Нет смысла приводить здесь нудные вычисления, показывающие, что это действительно дает прирост производительности — гораздо проще написать программу, которая это подсчитает. Получается порядка 3 × 107 чисел, остатки которых надо перемножить, вместо 10 000 × 30 000 = 3 × 108.
Однако всё же 3 × 107 × 25 = 7, 5 × 108 взятий по модулю. Понятно, что это всё равно не уложится в 5 секунд.
Вторая идея авторского решения.
Рассмотрим 4 модуля:
1224469897 = 7 × 17 × 37 × 47 × 61 × 97
1503325967 = 11 × 13 × 41 × 43 × 67 × 89
1336143462 = 2 × 3 × 23 × 31 × 53 × 71 × 83
937397015 = 5 × 19 × 29 × 59 × 73 × 79
Квадрат всех этих 4 чисел влезает в знаковый 64-битный тип данных и их произведение делится на все простые числа до 100. Для каждой из 10 000 цен чисел будем хранить остаток этой цены по каждому из четырех модулей. Легко посчитать остаток произведения и прибавить к нему константу. По четырём остаткам легко определить, какой будет минимальный делитель — перебрать 25 вариантов.
Итого, такая оптимизация дает асимптотику O(4 × (3 × 107)) = O(1, 2 × 108).
Здравствуйте!
Приглашаю Вас принять участие в сегодняшнем раунде, который кстати, будет последней возможностью на Codeforces потренироваться перед VK Cup, так что не упустите свой шанс =) Надеюсь, каждый найдет интересные для него задачи, у Вас не наступит взаимонепонимание с условиями и Ваши решения будут находится в полной гармонии с нашими тестами =)
Автор сегодняшнего раунда я, Валерий Самойлов, выпускник СПбГУ. Большое спасибо за помощь в подготовке задач Артёму Рахову (RAD) и Геральду Агапову (Gerald) (которому, кстати, был посвещён мой первый раунд: Codeforces Beta Round 79 (Div. 1 Only)) =)
Так же большое спасибо Марии Беловой за перевод условий и Александру Куприну (Alex_KPR) за вычитку условий и картинку =)
Обратите внимание, что в первом дивизионе разбалловка задач сегодня необычная:
500 — 1000 — 1500 — 2500 — 2500
Во втором дивизионе же такая же, как всегда:
500 — 1000 — 1500 — 2000 — 2500
Всем удачи!
По техническим причинам раунд отложен на полчаса. Регистрация закончится в 21:25.
Поздравляем победителей!
Первый дивизион:
Второй дивизион:
Опубликован полный разбор на русском.
Привет всем!
Рад приветствовать вас на очередном, 94, раунде Codeforces. Надеюсь, что несколько более раннее время проведения раунда не скажется отрицательно на ваших успехах =)
Автором задач сегодняшнего раунда являюсь я, выпускник СПбГУ, Валерий Самойлов. Это мой второй раунд на Codeforces. Надеюсь, что сегодня никто не пожалеет о своём участии. Большое спасибо RAD, который оказал неоценимую помощь при подготовке задач. Также спасибо Марии Беловой, переведшей условия на английский язык.
В этом раунде будет необычная разбалловка:
Див-1: 1000 - 1500 - 1500 - 2000 - 2500
Див-2: 500 - 1000 - 2000 - 2500 - 2500
Прошу не пугаться, все не так уж страшно =)
Раунд завершен, всем спасибо за участие!
Разбор ожидается завтра.
Победители:
Дивизион 1:
1. Egor
2. Gassa
3. dzhulgakov
5. tourist
6. tomek
7. LayCurse
8. a9108
9. Sereja
10. ftiasch
Дивизион 2
| Название |
|---|