Hi there.
The TopCoder Open 2023 Rules state that the first Online Round will be held on April 8, 2023 at 12:00 UTC-4, which is today.
But I still cannot see any options in the Active Contests menu of the Java Applet Arena. I've heard that the registration opens around 3-4 hours before the contest, so it should already be there, if my calculations are right.
Is it just me, or does anyone see the registration option?
P. S. There are no TopCoder entries at clist.by now, which is kinda strange. As I remember, in the previous years all TCO rounds were listed there.
UPD: It seems that dates specified in the Rules are no longer valid (hope the schedule would be updated).









 размера
размера 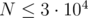 , а также
, а также 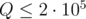 запросов вида
запросов вида 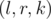 — определить количество элементов, больших
— определить количество элементов, больших 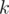 , на отрезке
, на отрезке 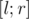 .
.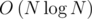 , ответ на запрос
, ответ на запрос 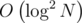 , online
, online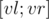 , хранится отсортированный вектор элементов массива
, хранится отсортированный вектор элементов массива 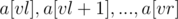 (в иностранных источниках такое дерево отрезков иногда называют merge tree). Объединять отсортированные вектора можно при помощи алгоритма STL merge().
(в иностранных источниках такое дерево отрезков иногда называют merge tree). Объединять отсортированные вектора можно при помощи алгоритма STL merge().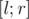 мы, как обычно, спускаемся к вершинам, подотрезки которых входят в целевой отрезок, и в каждой из этих вершин выполняем двоичный поиск, чтобы определить количество элементов, больших
мы, как обычно, спускаемся к вершинам, подотрезки которых входят в целевой отрезок, и в каждой из этих вершин выполняем двоичный поиск, чтобы определить количество элементов, больших 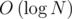 , online
, online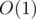 , если бы в каждой вершине была сохранена дополнительная информация.
, если бы в каждой вершине была сохранена дополнительная информация.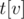 — отсортированный вектор, хранящийся в вершине
— отсортированный вектор, хранящийся в вершине  ,
, 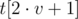 и
и 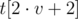 — отсортированные вектора, хранящиеся в её левом и правом потомках. Пусть в вершине
— отсортированные вектора, хранящиеся в её левом и правом потомках. Пусть в вершине 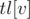 и
и 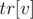 , такие что
, такие что 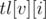 — индекс первого элемента, большего или равного
— индекс первого элемента, большего или равного 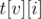 , в массиве
, в массиве 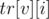 — аналогичный индекс в массиве
— аналогичный индекс в массиве  первого элемента, большего
первого элемента, большего 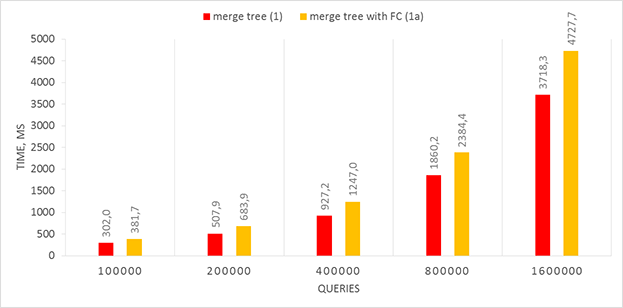
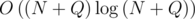 , ответ на запрос
, ответ на запрос 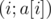 , то ответом на запрос
, то ответом на запрос 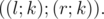
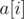 , для запросов —
, для запросов — 
 , offline
, offline , для концов запросов —
, для концов запросов —  ). По ординатам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек.
). По ординатам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек. , при обработке конца запроса добавляем к ответу сумму на отрезке
, при обработке конца запроса добавляем к ответу сумму на отрезке 
 , offline
, offline до
до  . Время обработки запроса при этом сократится от
. Время обработки запроса при этом сократится от 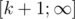 в версии
в версии  .
.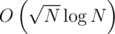 , online
, online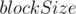 (получится
(получится 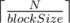 блоков). Отсортируем каждый из блоков.
блоков). Отсортируем каждый из блоков.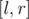 . В тех блоках, которые полностью покрываются отрезком запроса, количество чисел, больших
. В тех блоках, которые полностью покрываются отрезком запроса, количество чисел, больших 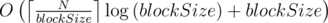 .
.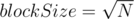 получаем классическую sqrt-декомпозицию, имеющую время обработки запроса
получаем классическую sqrt-декомпозицию, имеющую время обработки запроса 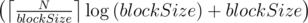 . При
. При 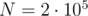 таким значением будет
таким значением будет 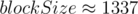 . Тем не менее, фактическое увеличение производительности по сравнению с sqrt-декомпозицией составляет ~5%, что влечёт общую нецелесообразность подобной оптимизации.
. Тем не менее, фактическое увеличение производительности по сравнению с sqrt-декомпозицией составляет ~5%, что влечёт общую нецелесообразность подобной оптимизации.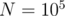 , заполненный случайными числами из диапазона
, заполненный случайными числами из диапазона 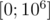 . Затем выполним
. Затем выполним 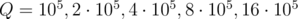 случайных KQUERY-запросов к данному массиву. Для каждого значения
случайных KQUERY-запросов к данному массиву. Для каждого значения 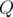 произведём 10 тестов, в качестве итогового времени возьмём среднее.
произведём 10 тестов, в качестве итогового времени возьмём среднее.
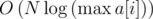 .
.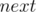 , такой что
, такой что 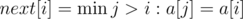 . Другими словами,
. Другими словами, 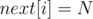 ).
).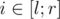 , что
, что 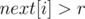 . Таким образом, результат запроса DQUERY
. Таким образом, результат запроса DQUERY 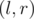 к массиву
к массиву 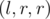 к массиву
к массиву 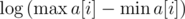 раз выше: из решений KQUERY с асимптотикой
раз выше: из решений KQUERY с асимптотикой 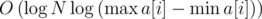
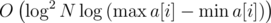 соответственно.
соответственно.
