One advanced topic in competitive programming are flows. The main challenge in flow problems lays often not in the algorithm itself, but in modelling the graph. To solve the project selection problem, we will model it as an instance of the minimum cut problem:
"You are given a directed graph with weighted edges. One node is designated as a source and another as a sink. Erase a set of edges of minimal total weight such that the source and the sink become disconnected. The source and the sink are considered to be disconnected if there no longer exists a directed path between them"
The minimum cut problem is equivalent to the maximum flow problem. Note that we can consider the maximum flow problem as a black-box that solves our instances of minimum cut. Thus, once we manage to reduce our problems to minimum cut, we can consider them solved.
The project selection problem
This problems is most often stated as:
"You are given a set of $$$N$$$ projects and $$$M$$$ machines. The $$$i$$$-th machine costs $$$q_i$$$. The $$$i$$$-th project yields $$$p_i$$$ revenue. Each project requires a set of machines. If multiple projects require the same machine, they can share the same one. Choose a set of machines to buy and projects to complete such that the sum of the revenues minus the sum of the costs is maximized."
It is quite inconvenient that for projects we get revenue and for machines we have to pay, so let's assume that we are paid in advance for the projects and that we have to give the money back if we don't manage to finish it. These $$$2$$$ formulations are clearly equivalent, yet the latter is easier to model.
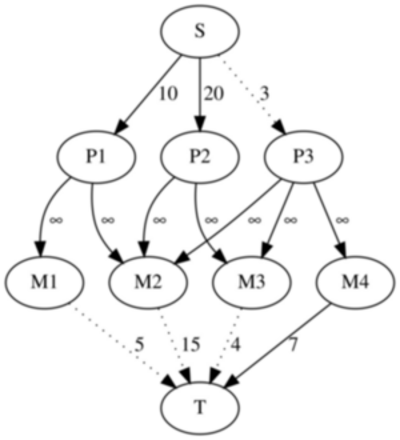
One simple way to model the above problem as a minimum cut is to create a graph with $$$N + M + 2$$$ vertices. Each vertex represents the source, the sink, a project or a machine. We will note the source as $$$S$$$, the sink as $$$T$$$, the i-th project as $$$P_i$$$ and the $$$i$$$-th machine as $$$M_i$$$. Then, add edges of weight $$$p_i$$$ between the source and the $$$i$$$-th project, edges of weight $$$q_i$$$ between the $$$i$$$-th machine and the sink, and edges of weight $$$\infty$$$ between each project and each of its required machines.
To reconstruct the solution, we will look at our minimum cut. If the edge between the source and the $$$i$$$-th project is cut, then we have to give the money back for the $$$i$$$-th project. If the edge between the $$$i$$$-th machine and the sink is cut, then we have to buy the $$$i$$$-th machine. It is easy to observe that for all dependencies between a project and a machine we will either buy the necessary machine or abandon the project since it would be impossible to cut the edge of weight $$$\infty$$$ between them.
Our model can be extended even to dependencies between $$$2$$$ projects or between $$$2$$$ machines. For example, let's say that projects $$$i$$$ is dependent on the project $$$j$$$. To represent this restriction we can add an edge of weight $$$\infty$$$ from $$$i$$$ to $$$j$$$. In essence, this edge tells that we cannot abandon project $$$j$$$ without also abandoning project $$$i$$$. If machine $$$i$$$ is dependent on machine $$$j$$$ we will have to add an edge in the graph from machine $$$i$$$ to machine $$$j$$$. We can even add dependencies between a machine and a project. It is easily seen from this, that there is actually no difference between a machine and a project other than their costs, in essence a machine is simply a project that costs money.
One last detail is that in the case of a time paradox such as project $$$1$$$ requires project $$$2$$$, project $$$2$$$ requires project $$$3$$$ and project $$$3$$$ requires project $$$1$$$ we can accidentally take them all using our model. If that is alright, then there is no problem. Otherwise, if the projects should be done in order and not all at once, we have to eliminate from the graph all nodes that belong to a cycle.
This project selection problem can appear in many forms and shapes. For example, the machines and projects can also be represented as clothes and outfits or as some other analogies. In these cases, we can easily recognize the connection to our original problem and formulate a solution extremely fast. However, often the "machines and projects" will not be represented by simple objects, but by more abstract concepts.
The Closure Problem
"You are given a directed graph. Each node has a certain weight. We define a closure as a set nodes such that there exists no edge that is directed from inside the closure to outside it. Find the closure with the maximal sum of weights."
The problem above is known in folklore as the closure problem. The closure requirement can be reformulated as follows. For each edge $$$(x, y)$$$ if $$$x$$$ is in the closure then $$$y$$$ has to also be included into the closure.
It is easy to see that this problem and the project selection problem are closely related, equivalent even. We can model the inclusion of a node in the closure as a "project". The restrictions can also be easily modelled as dependencies between our projects. Note that in this case there is no clear line between machines and projects as usual.
This problem can also be disguised as open-pit mining. Once again, it is easy to see the connection between these $$$2$$$ problems. Here is a sample submission implementing this idea.
A more abstract example
"You are given a graph with weighted nodes and weighted edges. Select a valid subset of nodes and edges with maximal weight. A subset is considered to be valid if for each included edge, both of its endpoints are also included in the subset"
We can consider the nodes as 'machines' and the edges as projects. Now, it is easy to see an edge being dependent on its $$$2$$$ endpoints is equivalent to a project being dependent on $$$2$$$ machines.
This problem can be found here and a sample submission can be found here. If we didn't know about the project selection problem, then this problem would have been much harder.
An even more abstract example
"You are planning to build housing on a street. There are n spots available on the street on which you can build a house. The spots are labeled from $$$1$$$ to $$$N$$$ from left to right. In each spot, you can build a house with an integer height between $$$0$$$ and $$$H$$$.
In each spot, if a house has height $$$a$$$, you can gain $$$a^2$$$ dollars from it.
The city has $$$M$$$ zoning restrictions though. The $$$i$$$-th restriction says that if the tallest house from spots $$$l_i$$$ to $$$r_i$$$ is strictly more than $$$x_i$$$, you must pay a fine of $$$c_i$$$.
You would like to build houses to maximize your profit (sum of dollars gained minus fines). Determine the maximum profit possible."
Let's reformulate the restrictions. For a restriction $$$(l_i, r_i, x_i, c_i)$$$ We can assume that we will get punished for all of them and that we will get our $$$c_i$$$ dollars back if all of our buildings in the range $$$[l_i, r_i]$$$ are smaller than or equal to $$$x_i$$$. With this small modification, we can now only gain money.
Let the maximal height be $$$H$$$. Let's say that originally all buildings start at height $$$H$$$ and there are multiple projects to reduce them. For example, the project $$$(i, h)$$$ represents reducing the $$$i$$$-th from height $$$h$$$ to $$$h - 1$$$ for the cost $$$h ^ 2 - (h - 1)^2$$$. The project $$$(i, h)$$$ is clearly dependent on the project $$$(i, h + 1)$$$. Let's also add our restrictions as projects. A restriction $$$(l_i, r_i, x_i, c_i)$$$ is equivalent to a project with profit $$$c_i$$$ dependent on the projects $$$(l_i, x_i)$$$, $$$(l_i + 1, x_i)$$$ $$$\dots$$$ $$$(r_i, x_i)$$$. In less formal terms, this means that we can regain our money if we reduce the $$$l_i$$$-th, $$$l_i + 1$$$-th $$$\dots$$$ $$$r_i$$$-th buildings to height $$$h_i$$$.
Note that this problem could have also been solved using dynamic programming. However, our solution has the major advantage that it is more easily generalizable. For example, we can easily modify this solution to account for restrictions applied on a non-consecutive set of buildings.
This problem can be found here and a sample submission implementing this idea can be found here. The editorial of this problem also describes another approach using maximum flow, that is more or less equivalent to the one presented here.
Conclusion
The project selection problem is an useful tool when modelling problems. Of course, these problems can be directly modelled using the maximum flow problem, however it is easier to use this already existing method.
Please share other problems that can be reduced to the project selection problem or similar modellings.