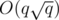APIO 2024 is scheduled to be held at May 18-19. For several years participants were allowed to take the exam at home, is it the same for this year?
Our national leader had sent an inquiry by email about two weeks ago, but got no response. So I thought maybe asking here would be faster, since some people should know about the rules.
It seems there is no APIO 2024 homepage yet, so even the basic rules are not available. I cannot find what the rules were for APIO 2023 since apio2023.org, apio2023.cn are all down and there is no searchable archive. APIO 2022 regulations say "Team leaders can do APIO 2022 Online or Onsite according to his country situation.", but we are not sure whether this is still relevant in 2024.









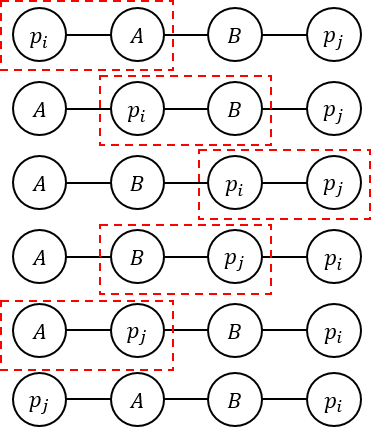
 ), erase
), erase 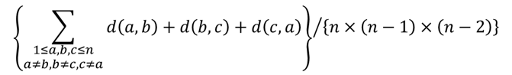
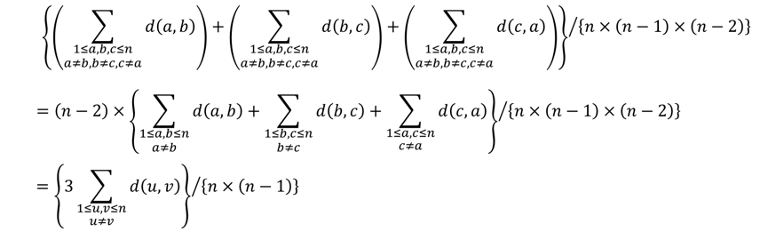
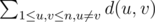 . I'll denote the sum as
. I'll denote the sum as 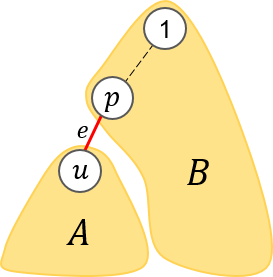
 is the set of vertices in the tree, and
is the set of vertices in the tree, and  is empty.
is empty.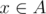 and
and 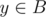 holds, the shortest path between
holds, the shortest path between 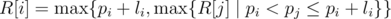 . This can be calculated by using a segment tree or using a stack, in decreasing order of
. This can be calculated by using a segment tree or using a stack, in decreasing order of 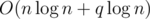 or
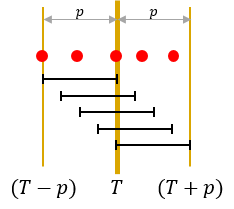
or  .
.
 holds.
holds. holds, using at most
holds, using at most 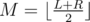 . Call
. Call 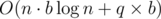 , because
, because 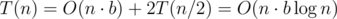 and the answer of the queries can be calculated in
and the answer of the queries can be calculated in 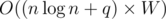 .
.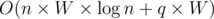 time, and it gets accepted in 546ms.
time, and it gets accepted in 546ms.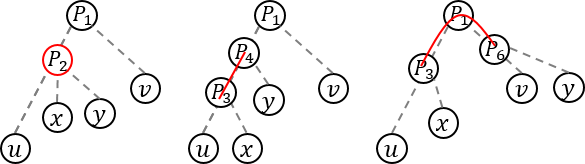
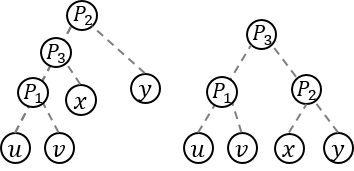
 . Then, there are two possible courses for JY:
. Then, there are two possible courses for JY:  and
and  ).
).
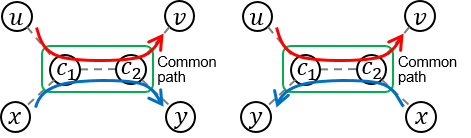
 .
. .
.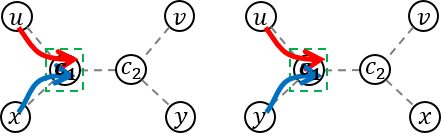
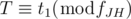
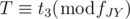
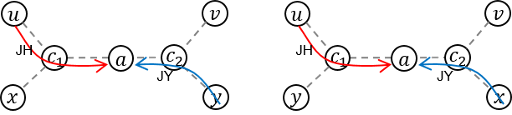
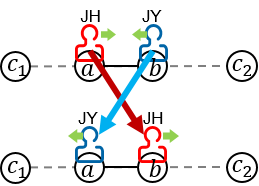
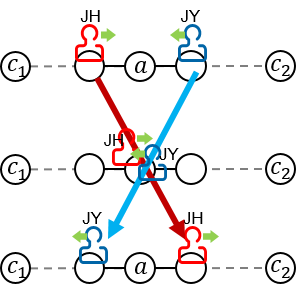
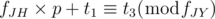 . In conclusion, we have to find the smallest
. In conclusion, we have to find the smallest 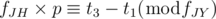
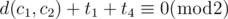
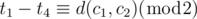
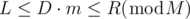 . This function can be implemented as follows.
. This function can be implemented as follows.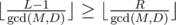 , it is "obvious" that there is no solution.
, it is "obvious" that there is no solution.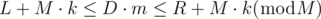 , we can write the inequality as
, we can write the inequality as 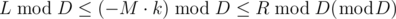
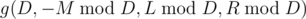 . We can easily calculate the smallest
. We can easily calculate the smallest 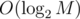 .
.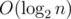 , so the time complexity per query is
, so the time complexity per query is 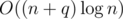
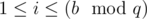 , assign
, assign 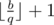 to
to 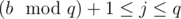 , assign
, assign 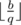 to
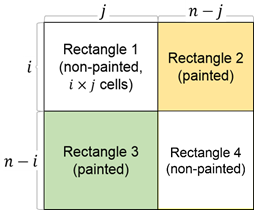
to 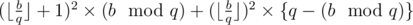 .
.
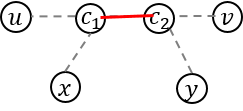
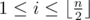 , make an edge between vertex
, make an edge between vertex 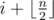 with weight 1.
with weight 1.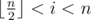 , make an edge between vertex
, make an edge between vertex 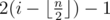 .
.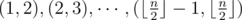 are all good pairs. In addition,
are all good pairs. In addition, 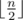 good pairs?
good pairs? .
. .
. , change the value of
, change the value of  , add
, add 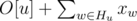 will be the answer. Because
will be the answer. Because  .
.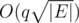
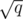 parts. For each block, use
parts. For each block, use 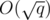 time to get the answer. If you want more details, please ask in the comments.
time to get the answer. If you want more details, please ask in the comments.