Author's Disclaimer: The following content is targeted towards those who are unfamiliar with range queries and how they work. If you are familiar with BITs, segment trees, and prefix sums, you will likely not learn anything new from reading this.

Author's Disclaimer #2: This is my first blog in a series of blogs I plan on writing that introduce various types of problems to beginner competitive programmers. That being said, I am by definition a beginner myself (regardless of my rating or competitive math experience, I have been doing this for less than a year). If you have any suggestions on how these could be improved, don't be afraid to speak up.

Note: Whenever I ask "why?" in parenthesis, this is not me asking because I don't know. This is me encouraging you to stop and think through why something I said is true. I don't want to just give answers, I want to provoke thought. This is how we learn. If you're stuck, feel free to ask in the comments. I am purposefully leaving implementations vague.

Basic Sum Queries (Prefix Sums)

Let's say we have some array $$$A$$$ = $$$A_{1}$$$, $$$A_{2}$$$, ..., $$$A_{n}$$$. Given two indices $$$i$$$ and $$$j$$$, we are tasked to find the following sum.

For those unfamiliar with the notation, this is simply $$$A_{i} + A_{i+1} + ... + A_{j}$$$.

We could do this by iterating over each element and adding it to a sum which is initially 0. The complexity of this is $$$O(n)$$$ (why?), which is too slow if we are processing a bunch of these queries.

Instead, we can generate some useful information about each index in $$$O(n)$$$ and then solve each query in $$$O(1)$$$. Let $$$dp_{i} = \sum\limits_{k=0}^{i} A_{k}$$$. Thus, $$$\sum\limits_{k=i}^{j} A_{k} = dp_{j} - dp_{i-1}$$$. Watch the $$$i=0$$$ case!

These $$$dp$$$ values can be stored in another array (or you can change the original array if you're feeling edgy that day and the problem allows it).

Note: This is technically really simple dp, but I'm in a small minority by actually notating it this way. Most people put psums in a different category.

This is the cses problem that correlates with this skill: https://cses.fi/problemset/task/1646

Next, try using prefix sums to solve this: 466C - Number of Ways

Sum Queries with a BIT

Note: BITs are probably more confusing than segment trees, so if this looks terrifying don't be afraid to skip this section.

Let's say we have the same task but an extra challenge is added. A new type of query is introduced in which we must add some value to one of the elements in the array. If we were to keep using the prefix sum method, suddenly we would have to rebuild the $$$dp$$$ array each time this type of query is called upon (why?). This is where a binary indexed tree (also known as a Fenwick tree) comes in. This uses bit operations (more precisely, powers of 2) to solve both types of queries in $$$O(\log n)$$$.

The main idea behind easily implementing this is that the largest power of two that divides some integer $$$k$$$ is k&(-k) (why?). We'll notate the largest power of two that divides $$$k$$$ as $$$☺(k)$$$ (this is obviously not official notation, please don't use it elsewhere or people will laugh at you). We then build a new array (we'll call it $$$T$$$ for tree) such that $$$T_{k}$$$ contains the sum of all elements in the sub-array that is of length $$$☺(k)$$$ and ends at index k.

To compute $$$\sum\limits_{i=0}^{k} A_{k}$$$, let $$$j = k$$$. Then, while(j > 0){ sum += T[j]; j -= j&(-j); }. As an exercise for the reader, try to think about how updating a value would work.

Both of these operations occur in $$$O(\log n)$$$ (why?).

This is a very confusing topic. Here is a diagram that may help (pulled from the cses handbook and edited for generalization purposes). This is also a good reminder to NOT make your BITs 0-based!

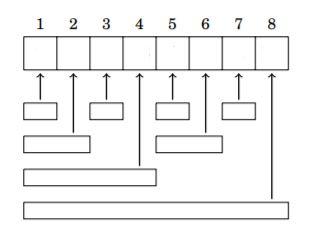
This is the cses problem that correlates with this skill: https://cses.fi/problemset/task/1648

Next, try to use a BIT to find the amount of inversions in an array. Don't be discouraged, this may be challenging! An inversion is a pair of indices $$$i < j$$$ such that $$$A_{i} > A{j}$$$.

Segment Trees (Iterative Implementation)

Let's say the task is no longer to find the sum of all elements in a range, but rather the minimum, maximum, or some other attribute of the range that would normally require an $$$O(n)$$$ iteration. Segment trees can do these efficiently ($$$O(\log n)$$$) and are often easier to understand than BITs (which can only handle sum queries). Before I get into detail, here's a diagram (again, copied and modified from the cses handbook) that should give you a pretty good idea of what we're working with.

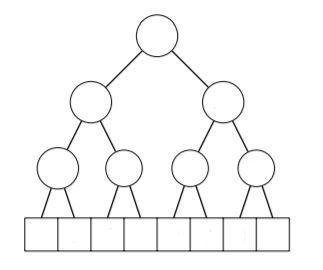
Let's say we're working with minimum range queries. In other words, what is the minimum value in the range $$$[a,b]$$$. We use the fact that each note in this diagram (the original array is the bottom row) is the minimum of the two nodes below it. We can actually store this segment tree in an array $$$T$$$ that is twice the size of the original array such that $$$T_{i} = min(T_{2i}, T_{2i+1})$$$. These, similarly to BITs, should NOT be zero based.

Let $$$n$$$ be the size of the original array and we want to find the minimum value in $$$[a,b]$$$. First, add $$$n$$$ to both $$$a$$$ and $$$b$$$ since the original array is actually stored in the second half of $$$T$$$, which is the data we will be working with. Then, we'll let res=INF where INF is some arbitrarily large value (infinity). Below is an iterative implementation of a minimum query with this segment tree we built.

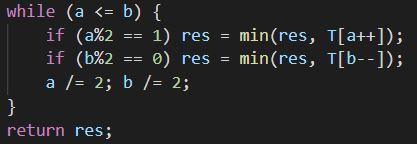
a /= 2; b /= 2; is simply moving up the tree (why?).